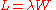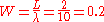Little's law
Encyclopedia
In the mathematical theory of queues
, Little's result, theorem, lemma, law or formula says:
It is a restatement of the Erlang formula, based on the work of Danish mathematician Agner Krarup Erlang
(1878 – 1929). Offered traffic E (in erlangs) is related to the call arrival rate, λ, and the average call-holding time, h, by:
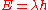
Although it looks intuitively reasonable, it's a quite remarkable result, as it implies that this behavior is entirely independent of any of the probability distribution
s involved, and hence requires no assumptions about the schedule according to which customers arrive or are serviced.
The first proof was published in 1961 by John Little, then at Case Western Reserve University
. His result applies to any system, and particularly, it applies to systems within systems. So in a bank, the customer line might be one subsystem, and each of the tellers another subsystem, and Little's result could be applied to each one, as well as the whole thing. The only requirements are that the system is stable and non-preemptive; this rules out transition states such as initial startup or shutdown.
In some cases it is possible to mathematically relate not only the average number in the system to the average wait but relate the entire probability distribution (and moments) of the number in the system to the wait.
This is a stable system, so the rate at which people enter the store is the rate at which they arrive at the store, and the rate at which they exit as well. We call this the arrival rate. By contrast, an arrival rate exceeding an exit rate would represent an unstable system, where the number of waiting customers in the store will gradually increase towards infinity.
Little's Law tells us that the average number of customers in the store, L, is the effective arrival rate, λ, times the average time that a customer spends in the store, W, or simply:
Assume customers arrive at the rate of 10 per hour and stay an average of 0.5 hour. This means we should find the average number of customers in the store at any time to be 5.
Now suppose the store is considering doing more advertising to raise the arrival rate to 20 per hour. The store must either be prepared to host an average of 10 occupants or must reduce the time each customer spends in the store to 0.25 hour. The store might achieve the latter by ringing up the bill faster or by adding more counters.
We can apply Little's Law to systems within the store. For example, the counter and its queue. Assume we notice that there are on average 2 customers in the queue and at the counter. We know the arrival rate is 10 per hour, so customers must be spending 0.2 hours on average checking out.
We can even apply Little's Law to the counter itself. The average number of people at the counter would be in the range (0, 1) since no more than one person can be at the counter at a time. In that case, the average number of people at the counter is also known as the utilisation of the counter.
It should be noted however, that because a store in reality generally has a limited amount of space, it cannot become unstable. Even if the arrival rate is much greater than the exit rate, the store will eventually start to overflow, and thus any new arriving customers will simply be rejected (and forced to go somewhere else or try again later) until there is once again free space available in the store. This is also the difference between the arrival rate and the effective arrival rate, where the arrival rate roughly corresponds to the rate of which customers arrive at the store, whereas the effective arrival rate corresponds to the rate of which customers enter the store. In a system with an infinite size and no loss, the two are however equal.
Queueing theory
Queueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
, Little's result, theorem, lemma, law or formula says:
- The long-term average number of customers in a stable system L is equal to the long-term average effective arrival rate, λ, multiplied by the (PalmPalm calculusIn the study of stochastic processes, Palm calculus, named after Swedish teletrafficist Conny Palm, is the study of the relationship between probabilities conditioned on a specified event and time average probabilities...
-)average time a customer spends in the system, W; or expressed algebraically: L = λW.
It is a restatement of the Erlang formula, based on the work of Danish mathematician Agner Krarup Erlang
Agner Krarup Erlang
Agner Krarup Erlang was a Danish mathematician, statistician and engineer, who invented the fields of traffic engineering and queueing theory....
(1878 – 1929). Offered traffic E (in erlangs) is related to the call arrival rate, λ, and the average call-holding time, h, by:
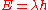
Although it looks intuitively reasonable, it's a quite remarkable result, as it implies that this behavior is entirely independent of any of the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s involved, and hence requires no assumptions about the schedule according to which customers arrive or are serviced.
The first proof was published in 1961 by John Little, then at Case Western Reserve University
Case Western Reserve University
Case Western Reserve University is a private research university located in Cleveland, Ohio, USA...
. His result applies to any system, and particularly, it applies to systems within systems. So in a bank, the customer line might be one subsystem, and each of the tellers another subsystem, and Little's result could be applied to each one, as well as the whole thing. The only requirements are that the system is stable and non-preemptive; this rules out transition states such as initial startup or shutdown.
In some cases it is possible to mathematically relate not only the average number in the system to the average wait but relate the entire probability distribution (and moments) of the number in the system to the wait.
Small example
Imagine a small store with a single counter and an area for browsing, where only one person can be at the counter at a time, and no one leaves without buying something. So the system is roughly:-
- Entrance → Browsing → Counter → Exit
This is a stable system, so the rate at which people enter the store is the rate at which they arrive at the store, and the rate at which they exit as well. We call this the arrival rate. By contrast, an arrival rate exceeding an exit rate would represent an unstable system, where the number of waiting customers in the store will gradually increase towards infinity.
Little's Law tells us that the average number of customers in the store, L, is the effective arrival rate, λ, times the average time that a customer spends in the store, W, or simply:
Assume customers arrive at the rate of 10 per hour and stay an average of 0.5 hour. This means we should find the average number of customers in the store at any time to be 5.
Now suppose the store is considering doing more advertising to raise the arrival rate to 20 per hour. The store must either be prepared to host an average of 10 occupants or must reduce the time each customer spends in the store to 0.25 hour. The store might achieve the latter by ringing up the bill faster or by adding more counters.
We can apply Little's Law to systems within the store. For example, the counter and its queue. Assume we notice that there are on average 2 customers in the queue and at the counter. We know the arrival rate is 10 per hour, so customers must be spending 0.2 hours on average checking out.
We can even apply Little's Law to the counter itself. The average number of people at the counter would be in the range (0, 1) since no more than one person can be at the counter at a time. In that case, the average number of people at the counter is also known as the utilisation of the counter.
It should be noted however, that because a store in reality generally has a limited amount of space, it cannot become unstable. Even if the arrival rate is much greater than the exit rate, the store will eventually start to overflow, and thus any new arriving customers will simply be rejected (and forced to go somewhere else or try again later) until there is once again free space available in the store. This is also the difference between the arrival rate and the effective arrival rate, where the arrival rate roughly corresponds to the rate of which customers arrive at the store, whereas the effective arrival rate corresponds to the rate of which customers enter the store. In a system with an infinite size and no loss, the two are however equal.
Applications
Software-performance testers have used Little's law to ensure that the observed performance results are not due to bottlenecks imposed by the testing apparatus. See:- Software Infrastructure Bottlenecks in J2EE by Deepak Goel
- Benchmarking Blunders and Things That Go Bump in the Night by Neil Gunther
See also
- List of eponymous laws (laws, adages, and other succinct observations or predictions named after persons)
External links
- A Proof of the Queueing Formula L = λ W, Sigman, K., Univ Columbia
- Little's Law, John D.C. Little and Stephen C. Graves, MIT