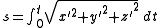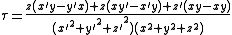2-Dimensional

Let be the standard Cartesian coordinates, and r and θ the standard polar coordinates.

To Cartesian coordinates from polar coordinates

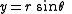
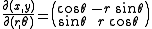
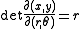
To polar coordinates from Cartesian coordinates

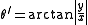
Note: solving for 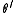returns the resultant angle in the first quadrant (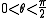). To find , one must refer to the original Cartesian coordinate, determine the quadrant in which lies (ex (3,-3) [Cartesian] lies in QIV), then use the following to solve for :

For in QI: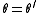

For 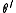in QII: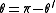

For 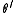in QIII: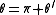

For 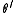in QIV: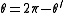

The value for 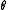must be solved for in this manner because for all values of 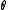, 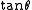is only defined for , and is periodic (with period ). This means that the inverse function will only give values in the domain of the function, but restricted to a single period. Hence, the range of the inverse function is only half a full circle.

Note that one can also use

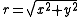
To Cartesian coordinates from log-polar coordinates

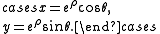
By using complex numbers 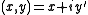, the transformation can be written as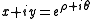


i.e. it is given by the complex exponential function.

To log-polar coordinates from Cartesian coordinates

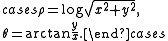
To Cartesian coordinates from bipolar coordinates

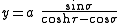
To Cartesian coordinates from two-center bipolar coordinates

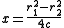
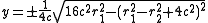
To polar coordinates from two-center bipolar coordinates

Where 2c is the distance between the poles.

To Cartesian coordinates from Cesàro equation

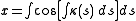
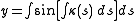
Arc length and curvature from Cartesian coordinates

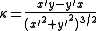
Arc length and curvature from polar coordinates

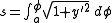
3-Dimensional

Let (x, y, z) be the standard Cartesian coordinates, and (ρ, θ, φ) the spherical coordinates, with θ the angle measured away from the +Z axis. As φ has a range of 360° the same considerations as in polar (2 dimensional) coordinates apply whenever an arctangent of it is taken. θ has a range of 180°, running from 0° to 180°, and does not pose any problem when calculated from an arccosine, but beware for an arctangent. If, in the alternative definition, θ is chosen to run from −90° to +90°, in opposite direction of the earlier definition, it can be found uniquely from an arcsine, but beware of an arccotangent. In this case in all formulas below all arguments in θ should have sine and cosine exchanged, and as derivative also a plus and minus exchanged.

All divisions by zero result in special cases of being directions along one of the main axes and are in practice most easily solved by observation.

From spherical coordinates

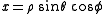
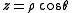
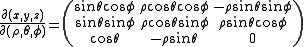
So for the volume element:

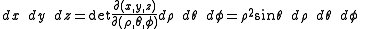
From cylindrical coordinates

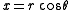
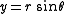
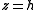
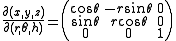
So for the volume element:

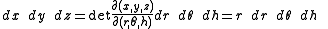
From Cartesian coordinates

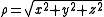
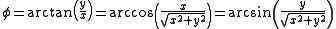
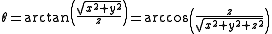
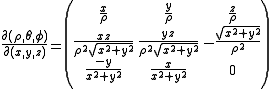
From cylindrical coordinates

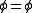
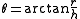
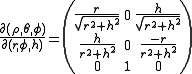
From Cartesian coordinates

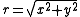
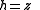
From spherical coordinates

Note: this section needs updating for consistency with nomenclature. A diagram should be included for this article showing what each variable represents. Usually \theta represents the polar angle for spherical coordinates and \phi the azimuthal angle for cylindrical coordinates. Here the two are mixed and could cause confusion. Someone please update.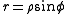

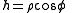
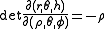
Arc length, curvature and torsion from cartesian coordinates