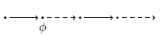
Linear temporal logic
Encyclopedia
In logic
, Linear temporal logic (LTL) is a modal
temporal logic
with modalities referring to time. In LTL, one can encode formulae about the future of paths
such as that a condition will eventually be true, that a condition will be true until another fact becomes true, etc. It is a fragment of the more complex CTL*, which also allows branching time and quantifiers. Subsequently LTL is sometimes called propositional temporal logic, abbreviated PTL.
Linear temporal logic (LTL) is a fragment of S1S.
LTL was first proposed for the formal verification
of computer programs by Amir Pnueli in 1977.
s AP, the logical operators ¬ and ∨, and the temporal
modal operator
s X and U.
Formally, the set of LTL formulas over AP is inductively defined as follows:
X is read as next and U is read as until. Sometimes, N is also used in place of X.
Other than these fundamental operators, there are additional logical and temporal operators defined in terms of the fundamental operators to write LTL formulas succinctly.
The additional logical operators are ∧, →, ↔, true, and false.
Following are the additional temporal operators.
This sequences can be viewed as a word on a path of a Kripke structure
(an ω-word over alphabet 2AP).
Let w=a1,a2,a3,... be such ω-word. Let w(i) = ai. Let wi = ai,ai+1,... , which is a suffix of w. Formally, the satisfaction relation between a word and an LTL formula is defined as follows:
between a word and an LTL formula is defined as follows:
We say an ω-word w satisfies LTL formula ψ when w ψ.
ψ.
The ω-language L(ψ) defined by ψ is the set {w | w ψ} of ω-words that satisfy ψ.
ψ} of ω-words that satisfy ψ.
A formula ψ is satisfiable if there exist a ω-word w such that w ψ.
ψ.
A formula ψ is valid if for each ω-word w over alphabet 2AP, w ψ.
ψ.
The additional logical operators are defined as follows:
The additional temporal operators R, F, and G are defined as follows:
Weak until
Some authors also define a weak until binary operator, denoted W, with semantics similar to that of the until operator but the stop condition is not required to occur (similar to release). It is sometimes useful since both U and R can be defined in terms of the weak until:
The semantics for the temporal operators are pictorially presented as follows.
†The symbols are used in the literature to denote these operators.
Using the above equivalences for negation propagation, it is possible to derive the normal form. This normal form allows R, true, false, and ∧ to appear in the formula, which are not fundamental operators of LTL. Note that the transformation to the negation normal form does not blow up the size of the formula. This normal form is useful in translation from LTL to Büchi automaton
.
s.
Computation tree logic (CTL) and Linear temporal logic (LTL) are both a subset of CTL*. CTL and LTL are not equivalent and they have a common subset, which is a proper subset of both CTL and LTL. For example,
An important way to model check is to express desired properties (such as the ones described above) using LTL operators and actually check if the model satisfies this property. One technique is to obtain a Büchi automaton
that is "equivalent" to the model and one that is "equivalent" to the negation of the property. The intersection of the two non-deterministic Büchi automata is empty if the model satisfies the property.
Expressing important properties in formal verification
There are two main types of properties that can be expressed using linear temporal logic: safety properties usually state that something bad never happens (G
 ), while liveness properties state that something good keeps happening (GF
), while liveness properties state that something good keeps happening (GF or G
or G F
F ). More generally: Safety properties are those for which every counterexample
). More generally: Safety properties are those for which every counterexample
has a finite prefix such that, however it is extended to an infinite path, it is still a counterexample. For liveness properties, on the other hand, every finite prefix of a counterexample can be extended to an infinite path that satisfies the formula.
Specification language
One of the applications of linear temporal logic is the specification of preference
s in the Planning Domain Definition Language
for the purpose of preference-based planning
.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, Linear temporal logic (LTL) is a modal
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
temporal logic
Temporal logic
In logic, the term temporal logic is used to describe any system of rules and symbolism for representing, and reasoning about, propositions qualified in terms of time. In a temporal logic we can then express statements like "I am always hungry", "I will eventually be hungry", or "I will be hungry...
with modalities referring to time. In LTL, one can encode formulae about the future of paths
Path (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
such as that a condition will eventually be true, that a condition will be true until another fact becomes true, etc. It is a fragment of the more complex CTL*, which also allows branching time and quantifiers. Subsequently LTL is sometimes called propositional temporal logic, abbreviated PTL.
Linear temporal logic (LTL) is a fragment of S1S.
LTL was first proposed for the formal verification
Formal verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of intended algorithms underlying a system with respect to a certain formal specification or property, using formal methods of mathematics .- Usage :Formal verification can be...
of computer programs by Amir Pnueli in 1977.
Syntax
LTL is built up from a finite set of propositional variablePropositional variable
In mathematical logic, a propositional variable is a variable which can either be true or false...
s AP, the logical operators ¬ and ∨, and the temporal
Temporal logic
In logic, the term temporal logic is used to describe any system of rules and symbolism for representing, and reasoning about, propositions qualified in terms of time. In a temporal logic we can then express statements like "I am always hungry", "I will eventually be hungry", or "I will be hungry...
modal operator
Modal operator
In modal logic, a modal operator is an operator which forms propositions from propositions. In general, a modal operator has the "formal" property of being non-truth-functional, and is "intuitively" characterised by expressing a modal attitude about the proposition to which the operator is applied...
s X and U.
Formally, the set of LTL formulas over AP is inductively defined as follows:
- if p ∈ AP then p is a LTL formula;
- if ψ and φ are LTL formulas then ¬ψ, φ ∨ ψ, X ψ and φ U ψ are LTL formulas.
X is read as next and U is read as until. Sometimes, N is also used in place of X.
Other than these fundamental operators, there are additional logical and temporal operators defined in terms of the fundamental operators to write LTL formulas succinctly.
The additional logical operators are ∧, →, ↔, true, and false.
Following are the additional temporal operators.
- G for always (globally)
- F for eventually (in the future)
- R for release
- W for weakly until
Semantics
An LTL formula can be satisfied by an infinite sequence of truth evaluations of variables in AP.This sequences can be viewed as a word on a path of a Kripke structure
Kripke structure
A Kripke structure is a type of nondeterministic finite state machine proposed by Saul Kripke , used in model checking to represent the behavior of a system.It is a simple abstract machine to capture an idea of a computing machine,...
(an ω-word over alphabet 2AP).
Let w=a1,a2,a3,... be such ω-word. Let w(i) = ai. Let wi = ai,ai+1,... , which is a suffix of w. Formally, the satisfaction relation
 between a word and an LTL formula is defined as follows:
between a word and an LTL formula is defined as follows:
- w
 p if p ∈ w(1)
p if p ∈ w(1) - w
 ¬ψ if w
¬ψ if w  ψ
ψ - w
 φ ∨ ψ if w
φ ∨ ψ if w  φ or w
φ or w  ψ
ψ - w
 X ψ if w2
X ψ if w2  ψ (in the next time step ψ must be true)
ψ (in the next time step ψ must be true) - w
 φ U ψ if there exist i > 0 such that wi
φ U ψ if there exist i > 0 such that wi  ψ and for all 0 < k < i, wk
ψ and for all 0 < k < i, wk  φ (φ must remain true until ψ becomes true)
φ (φ must remain true until ψ becomes true)
We say an ω-word w satisfies LTL formula ψ when w
 ψ.
ψ.The ω-language L(ψ) defined by ψ is the set {w | w
 ψ} of ω-words that satisfy ψ.
ψ} of ω-words that satisfy ψ.A formula ψ is satisfiable if there exist a ω-word w such that w
 ψ.
ψ.A formula ψ is valid if for each ω-word w over alphabet 2AP, w
 ψ.
ψ.The additional logical operators are defined as follows:
- φ ∧ ψ ≡ ¬(¬φ ∨ ¬ψ)
- φ → ψ ≡ ¬φ ∨ ψ
- φ ↔ ψ ≡ (φ → ψ) ∧ ( ψ → φ)
- true ≡ p ∨ ¬p, where p ∈ AP
- false ≡ ¬true
The additional temporal operators R, F, and G are defined as follows:
- φ R ψ ≡ ¬(¬φ U ¬ψ) ( ψ remains true until once φ becomes true. φ may never become true)
- F ψ ≡ true U ψ (eventually ψ becomes true)
- G ψ ≡ false R ψ ≡ ¬F ¬ψ (ψ always remains true)
Weak until
Some authors also define a weak until binary operator, denoted W, with semantics similar to that of the until operator but the stop condition is not required to occur (similar to release). It is sometimes useful since both U and R can be defined in terms of the weak until:
- φ W ψ ≡ (φ U ψ) ∨ G φ ≡ φ U (ψ ∨ G φ) ≡ ψ R (ψ ∨ φ)
- φ U ψ ≡ Fψ ∧ (φ W ψ)
- φ R ψ ≡ ψ W (ψ ∧ φ)
The semantics for the temporal operators are pictorially presented as follows.
| Textual | Symbolic† | Explanation | Diagram |
|---|---|---|---|
| Unary operators Unary operation In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A.... : |
|||
X  |
 |
neXt:  has to hold at the next state. has to hold at the next state. |
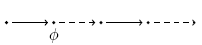 |
G  |
 |
Globally:  has to hold on the entire subsequent path. has to hold on the entire subsequent path. |
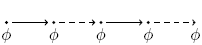 |
F  |
 |
Finally:  eventually has to hold (somewhere on the subsequent path). eventually has to hold (somewhere on the subsequent path). |
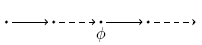 |
| Binary operators: | |||
 U U  |
 |
Until:  has to hold at least until has to hold at least until  , which holds at the current or a future position. , which holds at the current or a future position. |
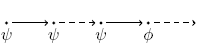 |
 R R  |
 |
Release:  has to be true until and including the point where has to be true until and including the point where  first becomes true; if first becomes true; if  never becomes true, never becomes true,  must remain true forever. must remain true forever. |
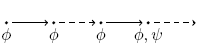 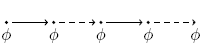 |
†The symbols are used in the literature to denote these operators.
Equivalences
Let Φ, ψ, and ρ be LTL formulas. The following tables list some of the useful equivalences which extend standard equivalences among the usual logical operators.| Distributivity | ||
|---|---|---|
| X (Φ ∨ ψ) ≡ (X Φ) ∨ (X ψ) | X (Φ ∧ ψ)≡ (X Φ) ∧ (X ψ) | X (Φ U ψ)≡ (X Φ) U (X ψ) |
| F (Φ ∨ ψ) ≡ (F Φ) ∨ (F ψ) | G (Φ ∧ ψ)≡ (G Φ) ∧ (G ψ) | |
| ρ U (Φ ∨ ψ) ≡ (ρ U Φ) ∨ (ρ U ψ) | (Φ ∧ ψ) U ρ ≡ (Φ U ρ) ∧ (ψ U ρ) | |
| Negation propagation | ||
|---|---|---|
| ¬X Φ ≡ X ¬Φ | ¬G Φ ≡ F ¬Φ | ¬F Φ ≡ G ¬Φ |
| ¬ (Φ U ψ) ≡ (¬Φ R ¬ψ) | ¬ (Φ R ψ) ≡ (¬Φ U ¬ψ) | |
| Special Temporal properties | ||
|---|---|---|
| F Φ ≡ F F Φ | G Φ ≡ G G Φ | Φ U ψ ≡ Φ U (Φ U ψ) |
| Φ U ψ ≡ ψ ∨ ( Φ ∧ X(Φ U ψ) ) | Φ W ψ ≡ ψ ∨ ( Φ ∧ X(Φ W ψ) ) | Φ R ψ ≡ ( ψ ∧ (Φ ∨ X(Φ R ψ) ) |
| G Φ ≡ Φ ∧ X(G Φ) | F Φ ≡ Φ ∨ X(F Φ) | |
Negation normal form
All the formulas of LTL can be transformed into negation normal form, where- all negations appear only in front of the atomic propositions,
- only other logical operators true, false, ∧, and ∨ can appear, and
- only the temporal operators X, U, and R can appear.
Using the above equivalences for negation propagation, it is possible to derive the normal form. This normal form allows R, true, false, and ∧ to appear in the formula, which are not fundamental operators of LTL. Note that the transformation to the negation normal form does not blow up the size of the formula. This normal form is useful in translation from LTL to Büchi automaton
Linear temporal logic to Büchi automaton
In formal verification,the model checking method needs to obtain a Büchi automaton from a Linear temporal logic formula.There are algorithms that translates a LTL formula to an equivalent BA...
.
Relations with other logics
LTL can be shown to be equivalent to the monadic first-order logic of order, FO[<]—a result known as Kamp's theorem— or equivalently star-free languageStar-free language
A regular language is said to be star-free if it can be described by a regular expression constructed from the letters of the alphabet, the empty set symbol, all boolean operators – including complementation – and concatenation but no Kleene star...
s.
Computation tree logic (CTL) and Linear temporal logic (LTL) are both a subset of CTL*. CTL and LTL are not equivalent and they have a common subset, which is a proper subset of both CTL and LTL. For example,
- No formula in CTL can define the language that is defined by LTL formula G(F p).
- No formula in LTL can define the language that is defined by CTL formula AG( p → (EXq ∧ EX¬q) ).
Applications
Automata theoretic Linear temporal logic model checkingAn important way to model check is to express desired properties (such as the ones described above) using LTL operators and actually check if the model satisfies this property. One technique is to obtain a Büchi automaton
Büchi automaton
In computer science and automata theory, a Büchi automaton is a type of ω-automaton, which extends a finite automaton to infinite inputs. It accepts an infinite input sequence iff there exists a run of the automaton that visits one of the final states infinitely often. Büchi automata recognize the...
that is "equivalent" to the model and one that is "equivalent" to the negation of the property. The intersection of the two non-deterministic Büchi automata is empty if the model satisfies the property.
Expressing important properties in formal verification
There are two main types of properties that can be expressed using linear temporal logic: safety properties usually state that something bad never happens (G

 ), while liveness properties state that something good keeps happening (GF
), while liveness properties state that something good keeps happening (GF or G
or G F
F ). More generally: Safety properties are those for which every counterexample
). More generally: Safety properties are those for which every counterexampleCounterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
has a finite prefix such that, however it is extended to an infinite path, it is still a counterexample. For liveness properties, on the other hand, every finite prefix of a counterexample can be extended to an infinite path that satisfies the formula.
Specification language
One of the applications of linear temporal logic is the specification of preference
Preference
-Definitions in different disciplines:The term “preferences” is used in a variety of related, but not identical, ways in the scientific literature. This makes it necessary to make explicit the sense in which the term is used in different social sciences....
s in the Planning Domain Definition Language
Planning Domain Definition Language
The Planning Domain Definition Language is an attempt to standardize planning domain and problem description languages. It was developed mainly to make the 1998/2000 International Planning Competitions possible....
for the purpose of preference-based planning
Preference-based planning
In artificial intelligence, preference-based planning is a form of automated planning and scheduling which focuses on producing plans that additionally satisfy as many user-specified preferences as possible. In many problem domains, a task can be accomplished by various sequences of actions...
.

