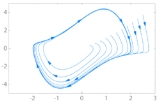
Limit-cycle
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of dynamical systems, a limit-cycle on a plane or a two-dimensional manifold is a closed trajectory
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
in phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such behavior is exhibited in some nonlinear systems. In the case where all the neighbouring trajectories approach the limit-cycle as time approaches infinity, it is called a stable
Stable manifold
In mathematics, and in particular the study of dynamical systems, the idea of stable and unstable sets or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor...
or attractive limit-cycle (ω-limit cycle). If instead all neighbouring trajectories approach it as time approaches negative infinity, it is an unstable or non-attractive limit-cycle (α-limit cycle).
Stable limit-cycles imply self sustained oscillations. Any small perturbation from the closed trajectory would cause the system to return to the limit-cycle, making the system stick to the limit-cycle.
As seen in the figure, trajectories for various initial states of this system converge to the limit cycle. Hence, this system exhibits self-sustained oscillations.
The number of limit cycles of a polynomial differential equation is the main object of the second part of Hilbert's sixteenth problem
Hilbert's sixteenth problem
Hilbert's 16th problem was posed by David Hilbert at the Paris conference of the International Congress of Mathematicians in 1900, together with the other 22 problems....
. Bendixson's theorem and the Poincaré-Bendixson theorem predict the absence or existence, respectively, of limit cycles of two-dimensional nonlinear dynamical systems.

