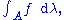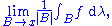Lebesgue differentiation theorem
Encyclopedia
In mathematics
, the Lebesgue differentiation theorem is a theorem of real analysis
, which states that for almost every point, the value of an integrable function is the limit of infinitesimal averages taken about the point. The theorem is named for Henri Lebesgue
.
which maps a measurable set A to the Lebesgue integral of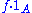
, where 
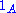denotes the characteristic function
of the set A. It is usually written
with λ the n–dimensional Lebesgue measure
.
The derivative of this integral at x is defined to be
where |B| denotes the volume (i.e., the Lebesgue measure) of a ball
B centered at x, and B → x means that the diameter of B tends to zero.
The Lebesgue differentiation theorem states that this derivative exists and is equal to f(x) at almost every
point x ∈ Rn. The points x for which this equality holds are called Lebesgue points. Since functions which are equal almost everywhere have the same integral over any set, this result is the best possible in the sense of recovering the function from integrals.
A more general version also holds. One may replace the balls B by a family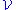
of sets U of bounded eccentricity. This means that there exists some fixed c > 0 such that each set U from the family is contained in a ball B with 
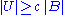. It is also assumed that every point x ∈ Rn is contained in arbitrarily small sets from 
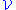. When these sets shrink to x, the same result holds: for almost every point x,
The family of cubes is an example of such a family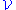
, as is the family 
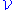(m) of rectangles in R2 such that the ratio of sides stays between m−1 and m, for some fixed m ≥ 1. If an arbitrary norm is given on Rn, the family of balls for the metric associated to the norm is another example.
The one-dimensional case was proved earlier by . If f is integrable on the real line, the function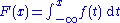
is almost everywhere differentiable, with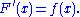
It is sufficient to prove that the set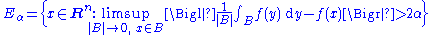
has measure 0 for all α > 0.
Let ε > 0 be given. Using the density
of continuous functions of compact support in L1(Rn), one can find such a function g satisfying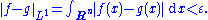
It is then helpful to rewrite the main difference as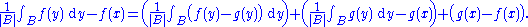
The first term can be bounded by the value at x of the maximal function for f − g, denoted here by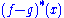
:
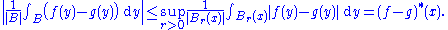
The second term disappears in the limit since g is a continuous function, and the third term is bounded by |f(x) − g(x)|. For the original difference to be greater than 2α in the limit, at least one of the first or third terms must be greater than α. However, the estimate on the Hardy–Littlewood function says that
for some constant An depending only upon the dimension n. The Markov inequality (also called Tchebyshev's inequality) says that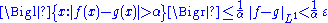
whence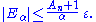
Since ε was arbitrary, it can be taken to be arbitrarily small, and the theorem follows.
is vital to the proof of this theorem; its role lies in proving the estimate for the Hardy-Littlewood maximal function.
The theorem also holds if balls are replaced, in the definition of the derivative, by families of sets with diameter tending to zero satisfying the Lebesgue's regularity condition, defined above as family of sets with bounded eccentricity. This follows since the same substitution can be made in the statement of the Vitali covering lemma.
, which equates a Riemann integrable function and the derivative of its (indefinite) integral. It is also possible to show a converse - that every differentiable function is equal to the integral of its derivative, but this requires a Henstock-Kurzweil
integral in order to be able to integrate an arbitrary derivative.
A special case of the Lebesgue differentiation theorem is the Lebesgue density theorem, which is equivalent to the differentiation theorem for characteristic functions of measurable sets. The density theorem is usually proved using a simpler method (e.g. see Measure and Category).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lebesgue differentiation theorem is a theorem of real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, which states that for almost every point, the value of an integrable function is the limit of infinitesimal averages taken about the point. The theorem is named for Henri Lebesgue
Henri Lebesgue
Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
.
Statement
For a Lebesgue integrable real or complex-valued function f on Rn, the indefinite integral is a set functionSet function
In mathematics, a set function is a function whose input is a set. The output is usually a number. Often the input is a set of real numbers, a set of points in Euclidean space, or a set of points in some measure space.- Examples :...
which maps a measurable set A to the Lebesgue integral of
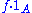, where 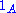denotes the characteristic functionCharacteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
of the set A. It is usually written
with λ the n–dimensional Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
.
The derivative of this integral at x is defined to be
where |B| denotes the volume (i.e., the Lebesgue measure) of a ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
B centered at x, and B → x means that the diameter of B tends to zero.
The Lebesgue differentiation theorem states that this derivative exists and is equal to f(x) at almost every
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
point x ∈ Rn. The points x for which this equality holds are called Lebesgue points. Since functions which are equal almost everywhere have the same integral over any set, this result is the best possible in the sense of recovering the function from integrals.
A more general version also holds. One may replace the balls B by a family
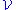of sets U of bounded eccentricity. This means that there exists some fixed c > 0 such that each set U from the family is contained in a ball B with 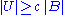. It is also assumed that every point x ∈ Rn is contained in arbitrarily small sets from 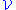. When these sets shrink to x, the same result holds: for almost every point x,
The family of cubes is an example of such a family
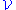, as is the family 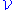(m) of rectangles in R2 such that the ratio of sides stays between m−1 and m, for some fixed m ≥ 1. If an arbitrary norm is given on Rn, the family of balls for the metric associated to the norm is another example.The one-dimensional case was proved earlier by . If f is integrable on the real line, the function
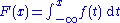
is almost everywhere differentiable, with
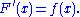
Proof
The theorem can be proved as a consequence of the weak–L1 estimates for the Hardy–Littlewood maximal function. The proof below follows which is the same as in .It is sufficient to prove that the set
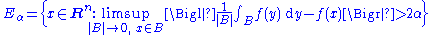
has measure 0 for all α > 0.
Let ε > 0 be given. Using the density
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
of continuous functions of compact support in L1(Rn), one can find such a function g satisfying
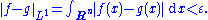
It is then helpful to rewrite the main difference as
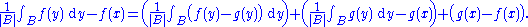
The first term can be bounded by the value at x of the maximal function for f − g, denoted here by
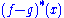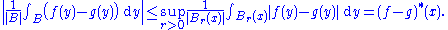
:The second term disappears in the limit since g is a continuous function, and the third term is bounded by |f(x) − g(x)|. For the original difference to be greater than 2α in the limit, at least one of the first or third terms must be greater than α. However, the estimate on the Hardy–Littlewood function says that
for some constant An depending only upon the dimension n. The Markov inequality (also called Tchebyshev's inequality) says that
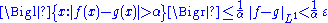
whence
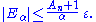
Since ε was arbitrary, it can be taken to be arbitrarily small, and the theorem follows.
Discussion of proof
The Vitali covering lemmaVitali covering lemma
In mathematics, the Vitali covering lemma is a combinatorial and geometric result commonly used in measure theory of Euclidean spaces. This lemma is an intermediate step, of independent interest, in the proof of the Vitali covering theorem. The covering theorem is credited to the Italian...
is vital to the proof of this theorem; its role lies in proving the estimate for the Hardy-Littlewood maximal function.
The theorem also holds if balls are replaced, in the definition of the derivative, by families of sets with diameter tending to zero satisfying the Lebesgue's regularity condition, defined above as family of sets with bounded eccentricity. This follows since the same substitution can be made in the statement of the Vitali covering lemma.
Discussion
This is an analogue, and a generalization, of the fundamental theorem of calculusFundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
, which equates a Riemann integrable function and the derivative of its (indefinite) integral. It is also possible to show a converse - that every differentiable function is equal to the integral of its derivative, but this requires a Henstock-Kurzweil
Henstock-Kurzweil integral
In mathematics, the Henstock–Kurzweil integral, also known as the Denjoy integral and the Perron integral, is one of a number of definitions of the integral of a function. It is a generalization of the Riemann integral which in some situations is more useful than the Lebesgue integral.This integral...
integral in order to be able to integrate an arbitrary derivative.
A special case of the Lebesgue differentiation theorem is the Lebesgue density theorem, which is equivalent to the differentiation theorem for characteristic functions of measurable sets. The density theorem is usually proved using a simpler method (e.g. see Measure and Category).