In
physicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the
Lamb shift, named after
Willis LambWillis Eugene Lamb, Jr. was an American physicist who won the Nobel Prize in Physics in 1955 together with Polykarp Kusch "for his discoveries concerning the fine structure of the hydrogen spectrum". Lamb and Kusch were able to precisely determine certain electromagnetic properties of the electron...
(1913–2008), is a small difference in
energyIn physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
between two
energy levelA quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
s
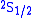and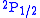
(in
term symbolIn quantum mechanics, the Russell-Saunders term symbol is an abbreviated description of the angular momentum quantum numbers in a multi-electron atom. It is related with the energy level of a given electron configuration. LS coupling is assumed...
notation) of the
hydrogen atomA hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
in
quantum electrodynamicsQuantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
(QED). According to
DiracPaul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
, the
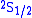and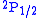
orbitals should have the same energies. However, the interaction between the electron and the vacuum causes a tiny energy shift on
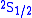. Lamb and Robert Retherford measured this shift in 1947, and this measurement provided the stimulus for renormalization theory to handle the divergences. It was the harbinger of modern QED as developed by
Julian SchwingerJulian Seymour Schwinger was an American theoretical physicist. He is best known for his work on the theory of quantum electrodynamics, in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order.Schwinger is recognized as one of the...
,
Richard FeynmanRichard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
, and Shinichiro Tomonaga. Lamb won the
Nobel Prize in PhysicsThe Nobel Prize in Physics is awarded once a year by the Royal Swedish Academy of Sciences. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895 and awarded since 1901; the others are the Nobel Prize in Chemistry, Nobel Prize in Literature, Nobel Peace Prize, and...
in 1955 for his discoveries related to the Lamb shift.
Derivation
This heuristic derivation of the electrodynamic level shift following Welton is from
Quantum Optics.
The fluctuation in the electric and magnetic fields associated with the vacuum perturbs the Coulomb potential due to the
atomic nucleusThe nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
. This
perturbationIn quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
causes a fluctuation in the position of the
electronThe electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
, which explains the energy shift. The difference of
potential energyIn physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
is given by
Since the fluctuations are isotropic,
.
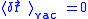
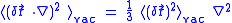So we can obtain
.
The classical
equation of motionEquations of motion are equations that describe the behavior of a system in terms of its motion as a function of time...
for the
electronThe electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
displacement
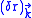induced by a single mode of the field of
wave vectorIn physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
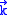and
frequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
is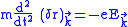
,
and this is valid only when the
frequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
is greater than
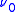in the Bohr orbit,
.
For the field oscillating at
,
,
therefore
.
By the summation over all
,
,
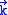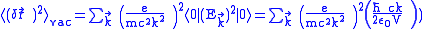where
.
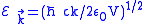The summation is changed into the integral because of the continuity of
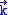, so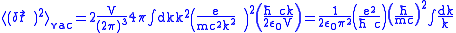
.
This result diverges when there is no limit about the integral. But this method is valid only when
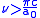, or equivalently
. It is also valid only for wavelengths longer than the
Compton wavelengthThe Compton wavelength is a quantum mechanical property of a particle. It was introduced by Arthur Compton in his explanation of the scattering of photons by electrons...
, or equivalently
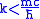. Therefore we can choose the upper and lower limit of the integral and these limits make the result converge.
.
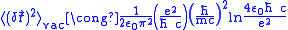For the
atomic orbitalAn atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...
and the Coulomb potential,
,
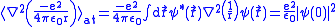since we know that
.
For p orbitals, the nonrelativistic wave function vanishes at the origin, so there is no energy shift. But for s orbitals there is some finite value at the origin,
,
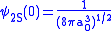where the
Bohr radiusThe Bohr radius is a physical constant, approximately equal to the most probable distance between the proton and electron in a hydrogen atom in its ground state. It is named after Niels Bohr, due to its role in the Bohr model of an atom...
is
.
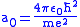Therefore
.
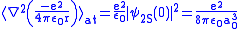Finally, the difference of the potential energy becomes
.
This shift is about 1 GHz, very similar with the observed energy shift.
Experimental work
In 1947 Willis Lamb and Robert Retherford carried out an experiment using
microwaveMicrowaves, a subset of radio waves, have wavelengths ranging from as long as one meter to as short as one millimeter, or equivalently, with frequencies between 300 MHz and 300 GHz. This broad definition includes both UHF and EHF , and various sources use different boundaries...
techniques to stimulate radio-frequency transitions between
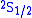and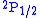
levels of hydrogen. By using lower frequencies than for optical transitions the
Doppler broadeningIn atomic physics, Doppler broadening is the broadening of spectral lines due to the Doppler effect caused by a distribution of velocities of atoms or molecules. Different velocities of the emitting particles result in different shifts, the cumulative effect of which is the line broadening.The...
could be neglected (Doppler broadening is proportional to the frequency). The energy difference Lamb and Retherford found was a rise
of about 1000 MHz of the
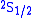level above the
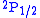level.
This particular difference is a one-loop effect of
quantum electrodynamicsQuantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
, and can be interpreted as the influence of virtual
photonIn physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s that have been emitted and re-absorbed by the atom. In quantum electrodynamics the electromagnetic field is quantized
and, like the
harmonic oscillatorIn classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
in
quantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, its lowest state is not zero. Thus, there exist small zero-point oscillations
that cause the
electronThe electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
to execute rapid oscillatory motions. The electron is "smeared out" and the radius is changed
from
to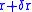
.
The Coulomb potential is therefore perturbed by a small amount and the degeneracy of the two energy levels is removed. The new potential can be approximated (using
atomic unitsAtomic units form a system of natural units which is especially convenient for atomic physics calculations. There are two different kinds of atomic units, which one might name Hartree atomic units and Rydberg atomic units, which differ in the choice of the unit of mass and charge. This article...
) as follows:
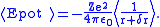
The Lamb shift itself is given by
with
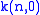around 13 varying slightly with
, and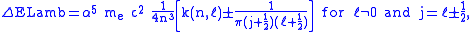
with
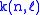a small number (< 0.05).
Lamb shift in the hydrogen spectrum
In 1947,
Hans BetheHans Albrecht Bethe was a German-American nuclear physicist, and Nobel laureate in physics for his work on the theory of stellar nucleosynthesis. A versatile theoretical physicist, Bethe also made important contributions to quantum electrodynamics, nuclear physics, solid-state physics and...
was the first to explain the Lamb shift in the hydrogen spectrum, and he thus laid the foundation for the modern development of
quantum electrodynamicsQuantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
. The Lamb shift currently provides a measurement of the
fine-structure constantIn physics, the fine-structure constant is a fundamental physical constant, namely the coupling constant characterizing the strength of the electromagnetic interaction. Being a dimensionless quantity, it has constant numerical value in all systems of units...
α to better than one part in a million, allowing a
precision test of quantum electrodynamicsQuantum electrodynamics , a relativistic quantum field theory of electrodynamics, is among the most stringently tested theories in physics....
.
A different perspective relates
ZitterbewegungZitterbewegung is a theoretical rapid motion of elementary particles, in particular electrons, that obey the Dirac equation...
to the Lamb shift.
External links