
Laguerre's method
Encyclopedia
In numerical analysis
, Laguerre's method is a root-finding algorithm
tailored to polynomial
s. In other words, Laguerre's method can be used to solve numerically the equation
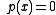
for a given polynomial p. One of the most useful properties of this method is that it is, from extensive empirical study, very close to being a "sure-fire" method, meaning that it is almost guaranteed to always converge to some root of the polynomial, no matter what initial guess is chosen. This method is named in honour of Edmond Laguerre
, a French mathematician.
states that every nth degree polynomial p can be written in the form
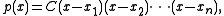
where xk are the roots of the polynomial. If we take the natural logarithm
of both sides, we find that

Denote the derivative by
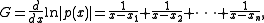
and the second derivative by

We then make what Acton calls a 'drastic set of assumptions', that the root we are looking for, say,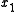 is a certain distance away from our guess
is a certain distance away from our guess  , and all the other roots are clustered together some distance away. If we denote these distances by
, and all the other roots are clustered together some distance away. If we denote these distances by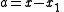
and
then our equation for G may be written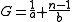
and that for H becomes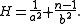
Solving these equations, we find that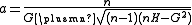 ,
,
where the square root of a complex number is chosen to produce larger absolute value of the denominator, or equivalently, to satisfy: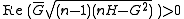 , where
, where 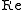 denotes real part of a complex number, and
denotes real part of a complex number, and 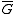 is a complex conjugation of
is a complex conjugation of 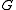 ;
;
or ,
,
where the square root of a complex number is chosen to have a non-negative real part.
For small values of p(x) this formula differs from the offset of the third order Halley's method
by an error of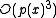 .
.
Note that, even if the 'drastic set of assumptions' does not work for some particular polynomial P, P can be transformed into a related polynomial Q for which the assumptions are correct, e.g. by adding a suitable complex number to give distinct roots distinct magnitudes if necessary (which it will be if some roots are complex conjugates), and then repeatedly applying the root squaring transformation used in Graeffe's method
enough times to make the smaller roots significantly smaller than the largest root (and so, clustered in comparison); the Graeffe's method
approximation can be used to start the new iteration for Laguerre's method
. An approximate root for P may then be obtained straightforwardly from that for Q.
whenever the initial guess x0 is close enough to the root x. On the other hand, if x is a multiple root then the convergence is only linear. This is obtained with the penalty of calculating values for the polynomial and its first and second derivatives at each stage of the iteration.
A major advantage of Laguerre's method is that it is almost guaranteed to converge to some root of the polynomial no matter where the initial approximation is chosen. This is in contrast to other methods such as the Newton-Raphson method
which may fail to converge for poorly chosen initial guesses. It may even converge to a complex root of the polynomial, because of the square root being taken in the calculation of a above may be of a negative number. This may be considered an advantage or a liability depending on the application to which the method is being used. Empirical evidence has shown that convergence failure is extremely rare, making this a good candidate for a general purpose polynomial root finding algorithm. However, given the fairly limited theoretical understanding of the algorithm, many numerical analysts are hesitant to use it as such, and prefer better understood methods such as the Jenkins-Traub method, for which more solid theory has been developed. Nevertheless, the algorithm is fairly simple to use compared to these other "sure-fire" methods, easy enough to be used by hand or with the aid of a pocket calculator when an automatic computer is unavailable. The speed at which the method converges means that one is only very rarely required to compute more than a few iterations to get high accuracy.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, Laguerre's method is a root-finding algorithm
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
tailored to polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s. In other words, Laguerre's method can be used to solve numerically the equation
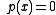
for a given polynomial p. One of the most useful properties of this method is that it is, from extensive empirical study, very close to being a "sure-fire" method, meaning that it is almost guaranteed to always converge to some root of the polynomial, no matter what initial guess is chosen. This method is named in honour of Edmond Laguerre
Edmond Laguerre
Edmond Nicolas Laguerre was a French mathematician, a member of the Académie française . His main works were in the areas of geometry and complex analysis. He also investigated orthogonal polynomials...
, a French mathematician.
Derivation
The fundamental theorem of algebraFundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
states that every nth degree polynomial p can be written in the form
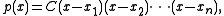
where xk are the roots of the polynomial. If we take the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of both sides, we find that

Denote the derivative by
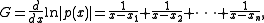
and the second derivative by

We then make what Acton calls a 'drastic set of assumptions', that the root we are looking for, say,
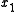 is a certain distance away from our guess
is a certain distance away from our guess  , and all the other roots are clustered together some distance away. If we denote these distances by
, and all the other roots are clustered together some distance away. If we denote these distances by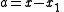
and

then our equation for G may be written
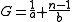
and that for H becomes
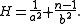
Solving these equations, we find that
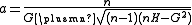 ,
,where the square root of a complex number is chosen to produce larger absolute value of the denominator, or equivalently, to satisfy:
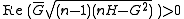 , where
, where 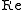 denotes real part of a complex number, and
denotes real part of a complex number, and 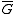 is a complex conjugation of
is a complex conjugation of 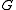 ;
;or
 ,
,where the square root of a complex number is chosen to have a non-negative real part.
For small values of p(x) this formula differs from the offset of the third order Halley's method
Halley's method
In numerical analysis, Halley’s method is a root-finding algorithm used for functions of one real variable with a continuous second derivative, i.e., C2 functions. It is named after its inventor Edmond Halley, who also discovered Halley's Comet....
by an error of
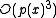 .
.Note that, even if the 'drastic set of assumptions' does not work for some particular polynomial P, P can be transformed into a related polynomial Q for which the assumptions are correct, e.g. by adding a suitable complex number to give distinct roots distinct magnitudes if necessary (which it will be if some roots are complex conjugates), and then repeatedly applying the root squaring transformation used in Graeffe's method
Graeffe's method
In mathematics, Graeffe's method or Dandelin–Graeffe method is an algorithm for finding all of the roots of a polynomial. It was developed independently by Germinal Pierre Dandelin in 1826 and Karl Heinrich Gräffe in 1837. Lobachevsky in 1834 also discovered the principal idea of the method....
enough times to make the smaller roots significantly smaller than the largest root (and so, clustered in comparison); the Graeffe's method
Graeffe's method
In mathematics, Graeffe's method or Dandelin–Graeffe method is an algorithm for finding all of the roots of a polynomial. It was developed independently by Germinal Pierre Dandelin in 1826 and Karl Heinrich Gräffe in 1837. Lobachevsky in 1834 also discovered the principal idea of the method....
approximation can be used to start the new iteration for Laguerre's method
Laguerre's method
In numerical analysis, Laguerre's method is a root-finding algorithm tailored to polynomials. In other words, Laguerre's method can be used to solve numerically the equation\ p = 0 for a given polynomial p...
. An approximate root for P may then be obtained straightforwardly from that for Q.
Definition
The above derivation leads to the following method:- Choose an initial guess
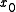
- For k = 0, 1, 2, …
- Calculate
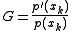
- Calculate
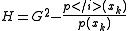
- Calculate
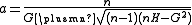 , where the sign is chosen to give the denominator with the larger absolute value, to avoid loss of significanceLoss of significanceLoss of significance is an undesirable effect in calculations using floating-point arithmetic. It occurs when an operation on two numbers increases relative error substantially more than it increases absolute error, for example in subtracting two large and nearly equal numbers. The effect is that...
, where the sign is chosen to give the denominator with the larger absolute value, to avoid loss of significanceLoss of significanceLoss of significance is an undesirable effect in calculations using floating-point arithmetic. It occurs when an operation on two numbers increases relative error substantially more than it increases absolute error, for example in subtracting two large and nearly equal numbers. The effect is that...
as iteration proceeds. - Set

- Calculate
- Repeat until a is small enough or if the maximum number of iterations has been reached.
Properties
If x is a simple root of the polynomial p, then Laguerre's method converges cubicallyRate of convergence
In numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
whenever the initial guess x0 is close enough to the root x. On the other hand, if x is a multiple root then the convergence is only linear. This is obtained with the penalty of calculating values for the polynomial and its first and second derivatives at each stage of the iteration.
A major advantage of Laguerre's method is that it is almost guaranteed to converge to some root of the polynomial no matter where the initial approximation is chosen. This is in contrast to other methods such as the Newton-Raphson method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
which may fail to converge for poorly chosen initial guesses. It may even converge to a complex root of the polynomial, because of the square root being taken in the calculation of a above may be of a negative number. This may be considered an advantage or a liability depending on the application to which the method is being used. Empirical evidence has shown that convergence failure is extremely rare, making this a good candidate for a general purpose polynomial root finding algorithm. However, given the fairly limited theoretical understanding of the algorithm, many numerical analysts are hesitant to use it as such, and prefer better understood methods such as the Jenkins-Traub method, for which more solid theory has been developed. Nevertheless, the algorithm is fairly simple to use compared to these other "sure-fire" methods, easy enough to be used by hand or with the aid of a pocket calculator when an automatic computer is unavailable. The speed at which the method converges means that one is only very rarely required to compute more than a few iterations to get high accuracy.

