Kripke semantics
Encyclopedia
Kripke semantics is a formal semantics
for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke
. It was first made for modal logic
s, and later adapted to intuitionistic logic
and other non-classical systems. The discovery of Kripke semantics was a breakthrough in the theory of non-classical logics, because the model theory
of such logics was nonexistent before Kripke.
of propositional variable
s, a set of truth-functional connectives
(in this article
and 
), and the modal operator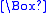 
("necessarily"). The modal operator 
("possibly") is the dual of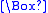 
and may be defined in terms of it like so: 
("possibly A" is defined as equivalent to "not necessarily not A").
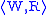, where W is a
non-empty set, and R is a binary relation
on W. Elements
of W are called nodes or worlds, and R is known as the
accessibility relation
.
A Kripke model is a triple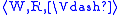
, where
is a Kripke frame, and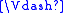 
is a relation between
nodes of W and modal formulas, such that:
We read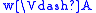
as “w satisfies
A”, “A is satisfied in w”, or
“w forces A”. The relation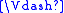
is called the
satisfaction relation, evaluation, or forcing
relation.
The satisfaction relation is uniquely determined by its
value on propositional variables.
A formula A is valid in:
We define Thm(C) to be the set of all formulas that are valid in
C. Conversely, if X is a set of formulas, let Mod(X) be the
class of all frames which validate every formula from X.
A modal logic (i.e., a set of formulas) L is sound with
respect to a class of frames C, if L ⊆ Thm(C). L is
complete wrt C if L ⊇ Thm(C).
relation reflects its syntactical counterpart, the consequence relation (derivability). It is vital to know which modal logics are sound and complete with respect to a class of Kripke frames, and to determine also which class that is.
For any class C of Kripke frames, Thm(C) is a normal modal logic
(in particular, theorems of the minimal normal modal logic, K, are valid in every Kripke model). However, the converse does not hold in general. There are Kripke incomplete normal modal logics, which is not a problem, because most of the modal systems studied are complete of classes of frames described by simple conditions.
A normal modal logic L corresponds to a class of frames C, if C = Mod(L). In other words, C is the largest class of frames such that L is sound wrt C. It follows that L is Kripke complete if and only if it is complete of its corresponding class.
Consider the schema T :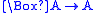
.
T is valid in any reflexive
frame
: if
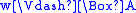, then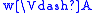 
since w R w. On the other hand, a frame which
validates T has to be reflexive: fix w ∈ W, and
define satisfaction of a propositional variable p as follows:
if and only if w R u. Then
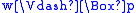, thus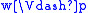 
by T, which means w R w using the definition of
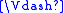. T corresponds to the class of reflexive
Kripke frames.
It is often much easier to characterize the corresponding class of
L than to prove its completeness, thus correspondence serves as a
guide to completeness proofs. Correspondence is also used to show
incompleteness of modal logics: suppose
L1 ⊆ L2 are normal modal logics that
correspond to the same class of frames, but L1 does not
prove all theorems of L2. Then L1 is
Kripke incomplete. For example, the schema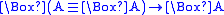
generates an incomplete logic, as it
corresponds to the same class of frames as GL (viz. transitive and
converse well-founded frames), but does not prove the GL-tautology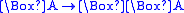
.
The table below is a list of common modal axioms together with their
corresponding classes. The naming of the axioms often varies.
Here is a list of several common modal systems. Frame conditions for
some of them were simplified: the logics are
complete with respect to the frame classes given in the table, but
they may correspond to a larger class of frames.
L, by an adaptation of the standard technique of using maximal consistent sets as models. Canonical Kripke models play a
role similar to the Lindenbaum–Tarski algebra
construction in algebraic
semantics.
A set of formulas is L-consistent if no contradiction can be derived from them using the axioms of L,
and Modus Ponens. A maximal L-consistent set (an L-MCS
for short) is an L-consistent set which has no proper
L-consistent superset.
The canonical model of L is a Kripke model
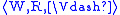, where W is the set of all L-MCS,
and the relations R and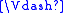
are as follows:
The canonical model is a model of L, as every L-MCS contains
all theorems of L. By Zorn's lemma
, each L-consistent set
is contained in an L-MCS, in particular every formula
unprovable in L has a counterexample in the canonical model.
The main application of canonical models are completeness proofs. Properties of the canonical model of K immediately imply completeness of K with respect to the class of all Kripke frames.
This argument does not work for arbitrary L, because there is no guarantee that the underlying frame of the canonical model satisfies the frame conditions of L.
We say that a formula or a set X of formulas is canonical
with respect to a property P of Kripke frames, if
A union of canonical sets of formulas is itself canonical.
It follows from the preceding discussion that any logic axiomatized by
a canonical set of formulas is Kripke complete, and
compact
.
The axioms T, 4, D, B, 5, H, G (and thus
any combination of them) are canonical. GL and Grz are not
canonical, because they are not compact. The axiom M by itself is
not canonical (Goldblatt, 1991), but the combined logic S4.1 (in
fact, even K4.1) is canonical.
In general, it is undecidable
whether a given axiom is
canonical. We know a nice sufficient condition: H.
Sahlqvist identified a broad class of formulas (now called
Sahlqvist formula
s) such that
This is a powerful criterion: for example, all axioms
listed above as canonical are (equivalent to) Sahlqvist formulas.
(FMP) if it is complete
with respect to a class of finite frames. An application of this
notion is the decidability
question: it
follows from
Post's theorem
that a recursively axiomatized modal logic L
which has FMP is decidable, provided it is decidable whether a given
finite frame is a model of L. In particular, every finitely
axiomatizable logic with FMP is decidable.
There are various methods for establishing FMP for a given logic.
Refinements and extensions of the canonical model construction often
work, using tools such as filtration or
unravelling. As another possibility,
completeness proofs based on cut-free
sequent calculi
usually produce finite models
directly.
Most of the modal systems used in practice (including all listed
above) have FMP.
In some cases, we can use FMP to prove Kripke completeness of a logic:
every normal modal logic is complete with respect to a class of
modal algebra
s, and a finite modal algebra can be transformed
into a Kripke frame. As an example, Robert Bull proved using this method
that every normal extension of S4.3 has FMP, and is Kripke
complete.
more than one modality. A Kripke frame for a language with
as the set of its necessity operators
consists of a non-empty set W equipped with binary relations
Ri for each i ∈ I. The definition of a
satisfaction relation is modified as follows:
A simplified semantics, discovered by Tim Carlson, is often used for
polymodal provability logic
s. A Carlson model is a structure
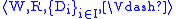
with a single accessibility relation R, and subsets
Di ⊆ W for each modality. Satisfaction is
defined as
Carlson models are easier to visualize and to work with than usual
polymodal Kripke models; there are, however, Kripke complete polymodal
logics which are Carlson incomplete.
follows the same
principles as the semantics of modal logic, but it uses a different
definition of satisfaction.
An intuitionistic Kripke model is a triple
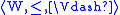, where 
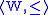is a partially ordered
Kripke frame, and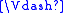
satisfies the following conditions:
The negation of A, ¬A, could be defined as an abbreviation for A → ⊥. If for all u such that w ≤ u, not u ⊩ A, then w ⊩ A → ⊥ is vacuously true
, so w ⊩ ¬A.
Intuitionistic logic is sound and complete with respect to its Kripke
semantics, and it has FMP.
language. A Kripke
model of L is a triple
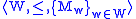, where
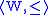is an intuitionistic Kripke frame, Mw is a
(classical) L-structure for each node w ∈ W, and
the following compatibility conditions hold whenever u ≤ v:
Given an evaluation e of variables by elements of Mw, we
define the satisfaction relation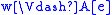
:
Here e(x→a) is the evaluation which gives x the
value a, and otherwise agrees with e.
See a slightly different formalization in.
in topos theory. That is, the 'local' aspect of existence for sections of a sheaf was a kind of logic of the 'possible'. Though this development was the work of a number of people, the name Kripke–Joyal semantics is often used in this connection.
, there are methods for
constructing a new Kripke model from other models.
The natural homomorphism
s in Kripke semantics are called
p-morphisms (which is short for pseudo-epimorphism, but the
latter term is rarely used). A p-morphism of Kripke frames
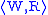and 
is a mapping
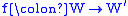such that
A p-morphism of Kripke models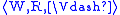
and
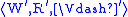is a p-morphism of their
underlying frames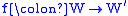
, which
satisfies
P-morphisms are a special kind of bisimulation
s. In general, a
bisimulation between frames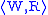
and
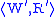is a relation
B ⊆ W × W’, which satisfies
the following “zig-zag” property:
A bisimulation of models is additionally required to preserve forcing
of atomic formula
s:
The key property which follows from this definition is that
bisimulations (hence also p-morphisms) of models preserve the
satisfaction of all formulas, not only propositional variables.
We can transform a Kripke model into a tree
using
unravelling. Given a model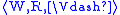
and a fixed
node w0 ∈ W, we define a model
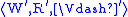, where W’ is the
set of all finite sequences
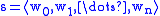such
that wi R wi+1 for all
i < n, and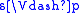
if and only if
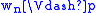for a propositional variable
p. The definition of the accessibility relation R’
varies; in the simplest case we put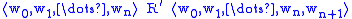
,
but many applications need the reflexive and/or transitive closure of
this relation, or similar modifications.
Filtration is a variant of a p-morphism. Let X be a set of
formulas closed under taking subformulas. An X-filtration of a
model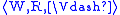
is a mapping f from W to a model
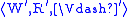such that
It follows that f preserves satisfaction of all formulas from
X. In typical applications, we take f as the projection
onto the quotient of W over the relation
As in the case of unravelling, the definition of the accessibility
relation on the quotient varies.
semantics.
, they give labeled transition systems, which model program execution
. Blackburn et al. thus claim because of this connection that modal languages are ideally suited in providing "internal, local perspective on relational structures." (p. xii)
Though the essential ideas of Kripke semantics were very much in the air by the time Kripke first published, Saul Kripke
's work on modal logic is rightly regarded as ground-breaking. Most importantly, it was Kripke who proved the completeness theorems for modal logic, and Kripke who identified the weakest normal modal logic.
Despite the seminal contribution of Kripke's work, many modal logicians deprecate the term Kripke semantics as disrespectful of the important contributions these other pioneers made. The other most widely used term possible world semantics is deprecated as inappropriate when applied to modalities other than possibility and necessity, such as in epistemic or deontic logic. Instead they prefer the terms relational semantics or frame semantics. The use of "semantics" for "model theory" has been objected to as well, on the grounds that it invites confusion with linguistic semantics: whether the apparatus of "possible worlds" that appears in models has anything to do with the linguistic meaning
of modal constructions in natural language is a contentious issue.
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke
Saul Kripke
Saul Aaron Kripke is an American philosopher and logician. He is a professor emeritus at Princeton and teaches as a Distinguished Professor of Philosophy at the CUNY Graduate Center...
. It was first made for modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
s, and later adapted to intuitionistic logic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
and other non-classical systems. The discovery of Kripke semantics was a breakthrough in the theory of non-classical logics, because the model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of such logics was nonexistent before Kripke.
Semantics of modal logic
The language of propositional modal logic consists of a countably infinite setCountable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
of propositional variable
Propositional variable
In mathematical logic, a propositional variable is a variable which can either be true or false...
s, a set of truth-functional connectives
Logical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
(in this article
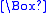and ), and the modal operator ("necessarily"). The modal operator ("possibly") is the dual of 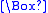and may be defined in terms of it like so: ("possibly A" is defined as equivalent to "not necessarily not A").Basic definitions
A Kripke frame or modal frame is a pair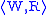, where W is anon-empty set, and R is a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
on W. Elements
of W are called nodes or worlds, and R is known as the
accessibility relation
Accessibility relation
In modal logic, an accessibility relation is a binary relation, written as R\,\! between possible worlds.-Description of terms:A statement in logic refers to a sentence that can be true or false...
.
A Kripke model is a triple
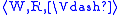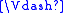, where is a Kripke frame, and is a relation betweennodes of W and modal formulas, such that:
-
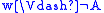if and only if 
, -
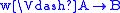if and only if 
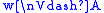or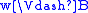 
, -
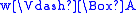if and only if 
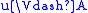for all 
such that 
.
We read
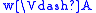as “w satisfiesA”, “A is satisfied in w”, or
“w forces A”. The relation
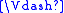is called thesatisfaction relation, evaluation, or forcing
Forcing (mathematics)
In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...
relation.
The satisfaction relation is uniquely determined by its
value on propositional variables.
A formula A is valid in:
- a model
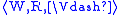, if 
for all w ∈ W, - a frame
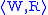, if it is valid in 
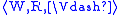for all possible choices of 
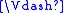, - a class C of frames or models, if it is valid in every member of C.
We define Thm(C) to be the set of all formulas that are valid in
C. Conversely, if X is a set of formulas, let Mod(X) be the
class of all frames which validate every formula from X.
A modal logic (i.e., a set of formulas) L is sound with
respect to a class of frames C, if L ⊆ Thm(C). L is
complete wrt C if L ⊇ Thm(C).
Correspondence and completeness
Semantics is useful for investigating a logic (i.e. a derivation system) only if the semantical entailmentEntailment
In logic, entailment is a relation between a set of sentences and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent...
relation reflects its syntactical counterpart, the consequence relation (derivability). It is vital to know which modal logics are sound and complete with respect to a class of Kripke frames, and to determine also which class that is.
For any class C of Kripke frames, Thm(C) is a normal modal logic
Normal modal logic
In logic, a normal modal logic is a set L of modal formulas such that L contains:* All propositional tautologies;* All instances of the Kripke schema: \Box\toand it is closed under:...
(in particular, theorems of the minimal normal modal logic, K, are valid in every Kripke model). However, the converse does not hold in general. There are Kripke incomplete normal modal logics, which is not a problem, because most of the modal systems studied are complete of classes of frames described by simple conditions.
A normal modal logic L corresponds to a class of frames C, if C = Mod(L). In other words, C is the largest class of frames such that L is sound wrt C. It follows that L is Kripke complete if and only if it is complete of its corresponding class.
Consider the schema T :
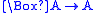.T is valid in any reflexive
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
frame
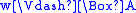: if, then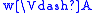 since w R w. On the other hand, a frame which
validates T has to be reflexive: fix w ∈ W, and
define satisfaction of a propositional variable p as follows:
if and only if w R u. Then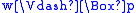, thus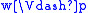 by T, which means w R w using the definition of
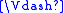. T corresponds to the class of reflexiveKripke frames.
It is often much easier to characterize the corresponding class of
L than to prove its completeness, thus correspondence serves as a
guide to completeness proofs. Correspondence is also used to show
incompleteness of modal logics: suppose
L1 ⊆ L2 are normal modal logics that
correspond to the same class of frames, but L1 does not
prove all theorems of L2. Then L1 is
Kripke incomplete. For example, the schema
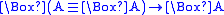generates an incomplete logic, as itcorresponds to the same class of frames as GL (viz. transitive and
converse well-founded frames), but does not prove the GL-tautology
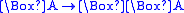.The table below is a list of common modal axioms together with their
corresponding classes. The naming of the axioms often varies.
| Name | Axiom | Frame condition |
|---|---|---|
| K |  |
N/A |
| T |  |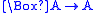
reflexive Reflexive relation In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:... :  |
| 4 |  |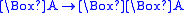
transitive Transitive relation In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c.... :  |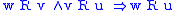
 |
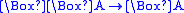dense Dense relation In mathematics, a binary relation R is said to be dense if, for all R-related x and y, there is a z such that x and z and also z and y are R-related.Formally:For example, a strict partial order... :  |
|
| D |  |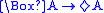
serial:  |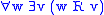
| B |  |
symmetric Symmetric relation In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:... :  |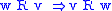
| 5 |  |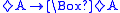
Euclidean Euclidean relation In mathematics, Euclidean relations are a class of binary relations that satisfy a weakened form of transitivity that formalizes Euclid's "Common Notion 1" in The Elements: things which equal the same thing also equal one another.-Definition:... :  |
| GL |  |
R transitive, R−1 well-founded |
| Grz |  |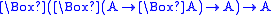
R reflexive and transitive, R−1−Id well-founded |
| H |  |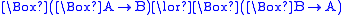
 |
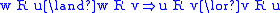| M |  |
(a complicated second-order Second-order logic In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory.... property) |
| G |  |
 |
 |
 |
|
 |
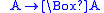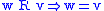partial function Partial function In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function... :  |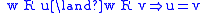
|
 |
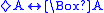function:  |
Here is a list of several common modal systems. Frame conditions for
some of them were simplified: the logics are
complete with respect to the frame classes given in the table, but
they may correspond to a larger class of frames.
| name | axioms | frame condition |
|---|---|---|
| K | — | all frames |
| T | T | reflexive |
| K4 | 4 | transitive |
| S4 | T, 4 | preorder Preorder In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders... |
| S5 | T, 5 or D, B, 4 | equivalence relation Equivalence relation In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell... |
| S4.3 | T, 4, H | total preorder |
| S4.1 | T, 4, M | preorder,  |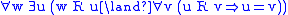
| S4.2 | T, 4, G | directed Directed set In mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤... preorder |
| GL Provability logic Provability logic is a modal logic, in which the box operator is interpreted as 'it is provable that'. The point is to capture the notion of a proof predicate of a reasonably rich formal theory, such as Peano arithmetic.... |
GL or 4, GL | finite strict partial order |
| Grz, S4Grz | Grz or T, 4, Grz | finite partial order |
| D | D | serial |
| D45 | D, 4, 5 | transitive, serial, and Euclidean |
Canonical models
For any normal modal logic L, a Kripke model (called the canonical model) can be constructed, which validates precisely the theorems ofL, by an adaptation of the standard technique of using maximal consistent sets as models. Canonical Kripke models play a
role similar to the Lindenbaum–Tarski algebra
Lindenbaum–Tarski algebra
In mathematical logic, the Lindenbaum–Tarski algebra of a logical theory T consists of the equivalence classes of sentences of the theory...
construction in algebraic
semantics.
A set of formulas is L-consistent if no contradiction can be derived from them using the axioms of L,
and Modus Ponens. A maximal L-consistent set (an L-MCS
for short) is an L-consistent set which has no proper
L-consistent superset.
The canonical model of L is a Kripke model
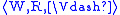, where W is the set of all L-MCS,and the relations R and
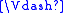are as follows:
-
if and only if for every formula 
, if 
then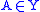 
, -
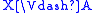if and only if 
.
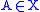The canonical model is a model of L, as every L-MCS contains
all theorems of L. By Zorn's lemma
Zorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
, each L-consistent set
is contained in an L-MCS, in particular every formula
unprovable in L has a counterexample in the canonical model.
The main application of canonical models are completeness proofs. Properties of the canonical model of K immediately imply completeness of K with respect to the class of all Kripke frames.
This argument does not work for arbitrary L, because there is no guarantee that the underlying frame of the canonical model satisfies the frame conditions of L.
We say that a formula or a set X of formulas is canonical
with respect to a property P of Kripke frames, if
- X is valid in every frame which satisfies P,
- for any normal modal logic L which contains X, the underlying frame of the canonical model of L satisfies P.
A union of canonical sets of formulas is itself canonical.
It follows from the preceding discussion that any logic axiomatized by
a canonical set of formulas is Kripke complete, and
compact
Compactness theorem
In mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model...
.
The axioms T, 4, D, B, 5, H, G (and thus
any combination of them) are canonical. GL and Grz are not
canonical, because they are not compact. The axiom M by itself is
not canonical (Goldblatt, 1991), but the combined logic S4.1 (in
fact, even K4.1) is canonical.
In general, it is undecidable
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
whether a given axiom is
canonical. We know a nice sufficient condition: H.
Sahlqvist identified a broad class of formulas (now called
Sahlqvist formula
Sahlqvist formula
In modal logic, Sahlqvist formulas are a certain kind of modal formula with remarkable properties. The Sahlqvist correspondence theorem states that every Sahlqvist formula is canonical, and corresponds to a first-order definable class of Kripke frames....
s) such that
- a Sahlqvist formula is canonical,
- the class of frames corresponding to a Sahlqvist formula is first-orderFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
definable, - there is an algorithm which computes the corresponding frame condition to a given Sahlqvist formula.
This is a powerful criterion: for example, all axioms
listed above as canonical are (equivalent to) Sahlqvist formulas.
Finite model property
A logic has the finite model propertyFinite model property
In logic, we say a logic L has the finite model property if there is a class of models M of L such that any non-theorem of L is falsified by some finite model in M...
(FMP) if it is complete
with respect to a class of finite frames. An application of this
notion is the decidability
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
question: it
follows from
Post's theorem
Post's theorem
In computability theory Post's theorem, named after Emil Post, describes the connection between the arithmetical hierarchy and the Turing degrees.- Background :The statement of Post's theorem uses several concepts relating to definability and recursion theory...
that a recursively axiomatized modal logic L
which has FMP is decidable, provided it is decidable whether a given
finite frame is a model of L. In particular, every finitely
axiomatizable logic with FMP is decidable.
There are various methods for establishing FMP for a given logic.
Refinements and extensions of the canonical model construction often
work, using tools such as filtration or
unravelling. As another possibility,
completeness proofs based on cut-free
sequent calculi
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
usually produce finite models
directly.
Most of the modal systems used in practice (including all listed
above) have FMP.
In some cases, we can use FMP to prove Kripke completeness of a logic:
every normal modal logic is complete with respect to a class of
modal algebra
Modal algebra
In algebra and logic, a modal algebra is a structure \langle A,\land,\lor,-,0,1,\Box\rangle such that*\langle A,\land,\lor,-,0,1\rangle is a Boolean algebra,...
s, and a finite modal algebra can be transformed
into a Kripke frame. As an example, Robert Bull proved using this method
that every normal extension of S4.3 has FMP, and is Kripke
complete.
Multimodal logics
Kripke semantics has a straightforward generalization to logics withmore than one modality. A Kripke frame for a language with
as the set of its necessity operatorsconsists of a non-empty set W equipped with binary relations
Ri for each i ∈ I. The definition of a
satisfaction relation is modified as follows:
-
if and only if 
A simplified semantics, discovered by Tim Carlson, is often used for
polymodal provability logic
Provability logic
Provability logic is a modal logic, in which the box operator is interpreted as 'it is provable that'. The point is to capture the notion of a proof predicate of a reasonably rich formal theory, such as Peano arithmetic....
s. A Carlson model is a structure
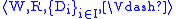
with a single accessibility relation R, and subsets
Di ⊆ W for each modality. Satisfaction is
defined as
-
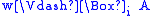if and only if 
Carlson models are easier to visualize and to work with than usual
polymodal Kripke models; there are, however, Kripke complete polymodal
logics which are Carlson incomplete.
Semantics of intuitionistic logic
Kripke semantics for the intuitionistic logicIntuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
follows the same
principles as the semantics of modal logic, but it uses a different
definition of satisfaction.
An intuitionistic Kripke model is a triple
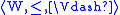, where 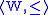is a partially orderedPartially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
Kripke frame, and
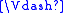satisfies the following conditions:
- if p is a propositional variable,
, and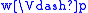 
, then 
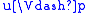(persistency condition), -
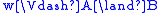if and only if 
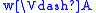and 
, -
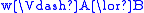if and only if 
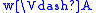or 
, -
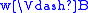if and only if for all 
, 
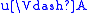implies 
, - not
.
The negation of A, ¬A, could be defined as an abbreviation for A → ⊥. If for all u such that w ≤ u, not u ⊩ A, then w ⊩ A → ⊥ is vacuously true
Vacuous truth
A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
, so w ⊩ ¬A.
Intuitionistic logic is sound and complete with respect to its Kripke
semantics, and it has FMP.
Intuitionistic first-order logic
Let L be a first-orderFirst-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
language. A Kripke
model of L is a triple
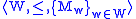, where 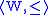is an intuitionistic Kripke frame, Mw is a(classical) L-structure for each node w ∈ W, and
the following compatibility conditions hold whenever u ≤ v:
- the domain of Mu is included in the domain of Mv,
- realizations of function symbols in Mu and Mv agree on elements of Mu,
- for each n-ary predicate P and elements a1,…,an ∈ Mu: if P(a1,…,an) holds in Mu, then it holds in Mv.
Given an evaluation e of variables by elements of Mw, we
define the satisfaction relation
:
-
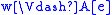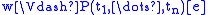if and only if 
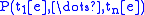holds in Mw, -
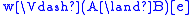if and only if 
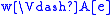and 
, -
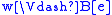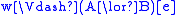if and only if 
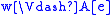or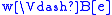 
, -
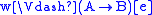if and only if for all 
, 
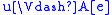implies 
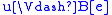, - not
, -
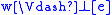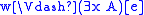if and only if there exists an 
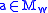such that 
, -
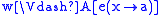if and only if for every 
and every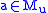 
, 
.
Here e(x→a) is the evaluation which gives x the
value a, and otherwise agrees with e.
See a slightly different formalization in.
Kripke–Joyal semantics
As part of the independent development of sheaf theory, it was realised around 1965 that Kripke semantics was intimately related to the treatment of existential quantificationExistential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
in topos theory. That is, the 'local' aspect of existence for sections of a sheaf was a kind of logic of the 'possible'. Though this development was the work of a number of people, the name Kripke–Joyal semantics is often used in this connection.
Model constructions
As in the classical model theoryModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, there are methods for
constructing a new Kripke model from other models.
The natural homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s in Kripke semantics are called
p-morphisms (which is short for pseudo-epimorphism, but the
latter term is rarely used). A p-morphism of Kripke frames
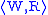and is a mapping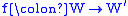 such that
- f preserves the accessibility relation, i.e., u R v implies f(u) R’ f(v),
- whenever f(u) R’ v’, there is a v ∈ W such that u R v and f(v) = v’.
A p-morphism of Kripke models
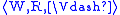and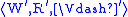 is a p-morphism of theirunderlying frames
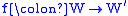, whichsatisfies
-
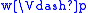if and only if 
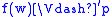, for any propositional variable p.
P-morphisms are a special kind of bisimulation
Bisimulation
In theoretical computer science a bisimulation is a binary relation between state transition systems, associating systems which behave in the same way in the sense that one system simulates the other and vice-versa....
s. In general, a
bisimulation between frames
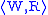and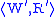 is a relationB ⊆ W × W’, which satisfies
the following “zig-zag” property:
- if u B u’ and u R v, there exists v’ ∈ W’ such that v B v’ and u’ R’ v’,
- if u B u’ and u’ R’ v’, there exists v ∈ W such that v B v’ and u R v.
A bisimulation of models is additionally required to preserve forcing
of atomic formula
Atomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
s:
- if w B w’, then
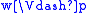if and only if 
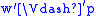, for any propositional variable p.
The key property which follows from this definition is that
bisimulations (hence also p-morphisms) of models preserve the
satisfaction of all formulas, not only propositional variables.
We can transform a Kripke model into a tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
using
unravelling. Given a model
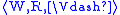and a fixednode w0 ∈ W, we define a model
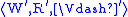, where W’ is theset of all finite sequences
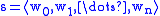suchthat wi R wi+1 for all
i < n, and
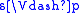if and only if 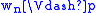for a propositional variablep. The definition of the accessibility relation R’
varies; in the simplest case we put
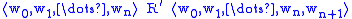,but many applications need the reflexive and/or transitive closure of
this relation, or similar modifications.
Filtration is a variant of a p-morphism. Let X be a set of
formulas closed under taking subformulas. An X-filtration of a
model
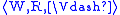is a mapping f from W to a model 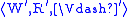such that
- f is a surjection,
- f preserves the accessibility relation, and (in both directions) satisfaction of variables p ∈ X,
- if f(u) R’ f(v) and
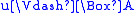, where 
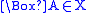, then 
.
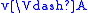It follows that f preserves satisfaction of all formulas from
X. In typical applications, we take f as the projection
onto the quotient of W over the relation
- u ≡X v if and only if for all A ∈ X,
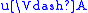if and only if 
.
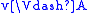As in the case of unravelling, the definition of the accessibility
relation on the quotient varies.
General frame semantics
The main defect of Kripke semantics is the existence of Kripke incomplete logics, and logics which are complete but not compact. It can be remedied by equipping Kripke frames with extra structure which restricts the set of possible valuations, using ideas from algebraic semantics. This gives rise to the general frameGeneral frame
In logic, general frames are Kripke frames with an additional structure, which are used to model modal and intermediate logics...
semantics.
Computer science applications
Blackburn et al. (2001) point out that because a relational structure is simply a set together with a collection of relations on that set, it is unsurprising that relational structures are to be found just about everywhere. As an example from theoretical computer scienceTheoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
, they give labeled transition systems, which model program execution
Computer program
A computer program is a sequence of instructions written to perform a specified task with a computer. A computer requires programs to function, typically executing the program's instructions in a central processor. The program has an executable form that the computer can use directly to execute...
. Blackburn et al. thus claim because of this connection that modal languages are ideally suited in providing "internal, local perspective on relational structures." (p. xii)
History and terminology
Kripke semantics does not originate with Kripke, but instead the idea of giving semantics in the style given above, that is based on valuations made that are relative to nodes, predates Kripke by a long margin:- Rudolf CarnapRudolf CarnapRudolf Carnap was an influential German-born philosopher who was active in Europe before 1935 and in the United States thereafter. He was a major member of the Vienna Circle and an advocate of logical positivism....
seems to have been the first to have the idea that one can give a possible world semantics for the modalities of necessity and possibility by means of giving the valuation function a parameter that ranges over Leibnizian possible worlds. Bayart develops this idea further, but neither gave recursive definitions of satisfaction in the style introduced by Tarski; - J.C.C. McKinsey and Alfred TarskiAlfred TarskiAlfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
developed an approach to modeling modal logics that is still influential in modern research, namely the algebraic approach, in which Boolean algebras with operators are used as models. Bjarni JónssonBjarni JónssonBjarni Jónsson is an Icelandic mathematician and logician working in universal algebra and lattice theory. He is emeritus Distinguished Professor of Mathematics at Vanderbilt University and the honorary editor in chief of Algebra Universalis...
and Tarski established the representability of Boolean algebras with operators in terms of frames. If the two ideas had been put together, the result would have been precisely frame models, which is to say Kripke models, years before Kripke. But no one (not even Tarski) saw the connection at the time. - Arthur PriorArthur PriorArthur Norman Prior was a noted logician and philosopher. Prior founded tense logic, now also known as temporal logic, and made important contributions to intensional logic, particularly in Prior .-Biography:Prior was entirely educated in New Zealand, where he was fortunate to have come under the...
, building on unpublished work of C. A. Meredith, developed a translation of sentential modal logic into classical predicate logic that, if he had combined it with the usual model theory for the latter, would have produced a model theory equivalent to Kripke models for the former. But his approach was resolutely syntactic and anti-model-theoretic. - Stig Kanger gave a rather more complex approach to the interpretation of modal logic, but one that contains many of the key ideas of Kripke's approach. He first noted the relationship between conditions on accessibility relations and Lewis-style axioms for modal logic. Kanger failed, however, to give a completeness proof for his system;
- Jaakko HintikkaJaakko HintikkaKaarlo Jaakko Juhani Hintikka is a Finnish philosopher and logician.Hintikka was born in Vantaa. After teaching for a number of years at Florida State University, Stanford, University of Helsinki, and the Academy of Finland, he is currently Professor of Philosophy at Boston University...
gave a semantics in his papers introducing epistemic logic that is a simple variation of Kripke's semantics, equivalent to the characterisation of valuations by means of maximal consistent sets. He doesn't give inference rules for epistemic logic, and so cannot give a completeness proof; - Richard MontagueRichard MontagueRichard Merett Montague was an American mathematician and philosopher.-Career:At the University of California, Berkeley, Montague earned an B.A. in Philosophy in 1950, an M.A. in Mathematics in 1953, and a Ph.D. in Philosophy 1957, the latter under the direction of the mathematician and logician...
had many of the key ideas contained in Kripke's work, but he did not regard them as significant, because he had no completeness proof, and so did not publish until after Kripke's papers had created a sensation in the logic community; - Evert Willem BethEvert Willem BethEvert Willem Beth was a Dutch philosopher and logician, whose work principally concerned the foundations of mathematics.- Biography :...
presented a semantics of intuitionistic logic based on trees, which closely resembles Kripke semantics, except for using a more cumbersome definition of satisfaction.
Though the essential ideas of Kripke semantics were very much in the air by the time Kripke first published, Saul Kripke
Saul Kripke
Saul Aaron Kripke is an American philosopher and logician. He is a professor emeritus at Princeton and teaches as a Distinguished Professor of Philosophy at the CUNY Graduate Center...
's work on modal logic is rightly regarded as ground-breaking. Most importantly, it was Kripke who proved the completeness theorems for modal logic, and Kripke who identified the weakest normal modal logic.
Despite the seminal contribution of Kripke's work, many modal logicians deprecate the term Kripke semantics as disrespectful of the important contributions these other pioneers made. The other most widely used term possible world semantics is deprecated as inappropriate when applied to modalities other than possibility and necessity, such as in epistemic or deontic logic. Instead they prefer the terms relational semantics or frame semantics. The use of "semantics" for "model theory" has been objected to as well, on the grounds that it invites confusion with linguistic semantics: whether the apparatus of "possible worlds" that appears in models has anything to do with the linguistic meaning
Linguistic meaning
The nature of meaning, its definition, elements, and types, was discussed by philosophers Aristotle, Augustine, and Aquinas. According to them 'meaning is a relationship between two sorts of things: signs and the kinds of things they mean '. One term in the relationship of meaning necessarily...
of modal constructions in natural language is a contentious issue.
External links
- The Stanford Encyclopedia of Philosophy: "Modal Logic" – by James Garson.
- Intuitionistic Logic. Written by Joan Moschovakis. Published in Stanford Encyclopedia of Philosophy.
- Detlovs and Podnieks, K., "Constructive Propositional Logic — Kripke Semantics." Chapter 4.4 of Introduction to Mathematical Logic. N.B: Constructive = intuitionistic.
- Burgess, John P., "Kripke Models."