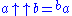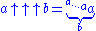Knuth's up-arrow notation
Encyclopedia
In mathematics
, Knuth's up-arrow notation is a method of notation for very large integer
s, introduced by Donald Knuth
in 1976. It is closely related to the Ackermann function
and especially to the hyperoperation
sequence. The idea is based on the fact that multiplication
can be viewed as iterated
addition
and exponentiation
as iterated multiplication
. Continuing in this manner leads to iterated exponentiation
(tetration) and to the remainder of the hyperoperation sequence, which is commonly denoted using Knuth arrow notation.
, multiplication
and exponentiation
are naturally extended into a sequence of hyperoperations as follows.
Multiplication
by a natural number
is defined as iterated addition
:
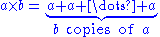
For example,
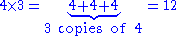
Exponentiation
for a natural power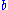
is defined as iterated multiplication, which Knuth denoted by a single up-arrow:
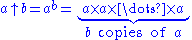
For example,
To extend the sequence of operations beyond exponentiation, Knuth defined a “double arrow” operator to denote iterated exponentiation (tetration
):
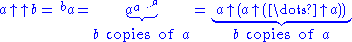
For example,
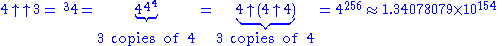
Here and below evaluation is to take place from right to left, as Knuth's arrow operators (just like exponentiation) are defined to be right-associative.
According to this definition,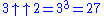
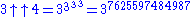
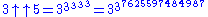
This already leads to some fairly large numbers, but Knuth extended the notation. He went on to define a “triple arrow” operator for iterated application of the “double arrow” operator (also known as pentation
):
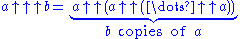
followed by a 'quadruple arrow' operator (also known as hexation):
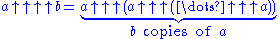
and so on. The general rule is that an
-arrow operator expands into a right-associative series of (
)-arrow operators. Symbolically,
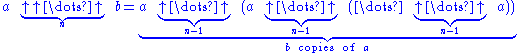
Examples:
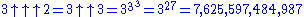
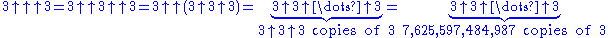
The notation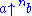
is commonly used to denote 
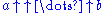with n arrows.
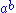, the notation for exponentiation is usually to write the exponent 
as a superscript to the base number 
. But many environments — such as programming language
s and plain-text e-mail
— do not support such two-dimensional layout. People have adopted the linear notation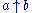
for such environments; the up-arrow suggests 'raising to the power of'. If the character set doesn't contain an up arrow, the caret
^ is used instead.
The superscript notation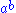
doesn't lend itself well to generalization, which explains why Knuth chose to work from the inline notation 
instead.
using the familiar superscript notation gives a power tower.
If b is a variable (or is too large), the power tower might be written using dots and a note indicating the height of the tower.
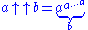
Continuing with this notation,
could be written with a stack of such power towers, each describing the size of the one above it.
Again, if b is a variable or is too large, the stack might be written using dots and a note indicating its height.
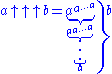
Furthermore,
might be written using several columns of such stacks of power towers, each column describing the number of power towers in the stack to its left:
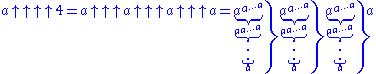
And more generally:
This might be carried out indefinitely to represent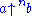
as iterated exponentiation of iterated exponentiation for any a, n and b (although it clearly becomes rather cumbersome).
notation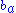
allows us to make these diagrams slightly simpler while still employing a geometric representation (we could call these tetration towers).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Knuth's up-arrow notation is a method of notation for very large integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, introduced by Donald Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
in 1976. It is closely related to the Ackermann function
Ackermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
and especially to the hyperoperation
Hyperoperation
In mathematics, the hyperoperation sequenceis an infinite sequence of arithmetic operations that starts with the unary operation of successor, then continues with the binary operations of addition, multiplication and exponentiation, after which the sequence proceeds with further binary operations...
sequence. The idea is based on the fact that multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
can be viewed as iterated
Iteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
as iterated multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
. Continuing in this manner leads to iterated exponentiation
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
(tetration) and to the remainder of the hyperoperation sequence, which is commonly denoted using Knuth arrow notation.
Introduction
The ordinary arithmetical operations of additionAddition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
and exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
are naturally extended into a sequence of hyperoperations as follows.
Multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
by a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
is defined as iterated addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
:
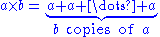
For example,
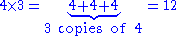
Exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
for a natural power
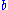is defined as iterated multiplication, which Knuth denoted by a single up-arrow: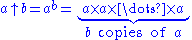For example,
To extend the sequence of operations beyond exponentiation, Knuth defined a “double arrow” operator to denote iterated exponentiation (tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
):
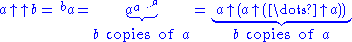
For example,
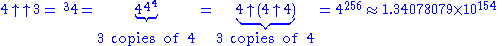
Here and below evaluation is to take place from right to left, as Knuth's arrow operators (just like exponentiation) are defined to be right-associative.
According to this definition,
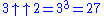
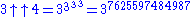
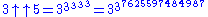
- etc.
This already leads to some fairly large numbers, but Knuth extended the notation. He went on to define a “triple arrow” operator for iterated application of the “double arrow” operator (also known as pentation
Pentation
Pentation is the operation of repeated tetration, just as tetration is the operation of repeated exponentation and is a hyperoperation. It is non-commutative, and therefore has two inverse functions, which might be named the penta-root and the penta-logarithm...
):
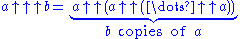
followed by a 'quadruple arrow' operator (also known as hexation):
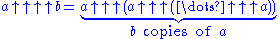
and so on. The general rule is that an
-arrow operator expands into a right-associative series of ()-arrow operators. Symbolically,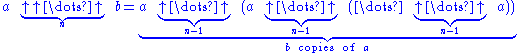Examples:
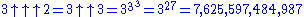
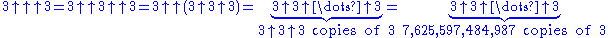
The notation
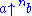is commonly used to denote 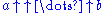with n arrows.Notation
In expressions such as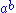, the notation for exponentiation is usually to write the exponent as a superscript to the base number . But many environments — such as programming languageProgramming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s and plain-text e-mail
E-mail
Electronic mail, commonly known as email or e-mail, is a method of exchanging digital messages from an author to one or more recipients. Modern email operates across the Internet or other computer networks. Some early email systems required that the author and the recipient both be online at the...
— do not support such two-dimensional layout. People have adopted the linear notation
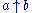for such environments; the up-arrow suggests 'raising to the power of'. If the character set doesn't contain an up arrow, the caretCaret
Caret usually refers to the spacing symbol ^ in ASCII and other character sets. In Unicode, however, the corresponding character is , whereas the Unicode character named caret is actually a similar but lowered symbol: ....
^ is used instead.
The superscript notation
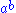doesn't lend itself well to generalization, which explains why Knuth chose to work from the inline notation instead.Writing out up-arrow notation in terms of powers
Attempting to write using the familiar superscript notation gives a power tower.- For example:
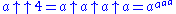
If b is a variable (or is too large), the power tower might be written using dots and a note indicating the height of the tower.
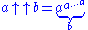
Continuing with this notation,
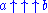could be written with a stack of such power towers, each describing the size of the one above it.Again, if b is a variable or is too large, the stack might be written using dots and a note indicating its height.
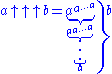
Furthermore,
might be written using several columns of such stacks of power towers, each column describing the number of power towers in the stack to its left: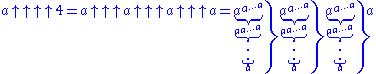And more generally:
This might be carried out indefinitely to represent
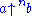as iterated exponentiation of iterated exponentiation for any a, n and b (although it clearly becomes rather cumbersome).Using tetration
The tetrationTetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
notation
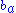allows us to make these diagrams slightly simpler while still employing a geometric representation (we could call these tetration towers).
-
Finally, as an example, the fourth Ackermann number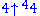
could be represented as:
-
Generalizations
Some numbers are so large that multiple arrows of Knuth's up-arrow notation become too cumbersome; then an n-arrow operator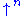
is useful (and also for descriptions with a variable number of arrows), or equivalently, hyper operators.
Some numbers are so large that even that notation is not sufficient. Graham's numberGraham's numberGraham's number, named after Ronald Graham, is a large number that is an upper bound on the solution to a certain problem in Ramsey theory.The number gained a degree of popular attention when Martin Gardner described it in the "Mathematical Games" section of Scientific American in November 1977,...
is an example. The Conway chained arrow notationConway chained arrow notationConway chained arrow notation, created by mathematician John Horton Conway, is a means of expressing certain extremely large numbers. It is simply a finite sequence of positive integers separated by rightward arrows, e.g. 2 → 3 → 4 → 5 → 6.As with most...
can then be used: a chain of three elements is equivalent with the other notations, but a chain of four or more is even more powerful.
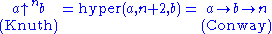
It is generally suggested that Knuth's arrow should be used for smaller magnitude numbers, and the chained arrow or hyper operators for larger ones.
Definition
The up-arrow notation is formally defined by
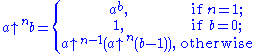
for all integers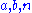
with 
.
All up-arrow operators (including normal exponentiation,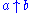
) are right associative, i.e. evaluation is to take place from right to left in an expression that contains two or more such operators. For example, 
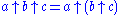, not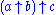 
; for example
is 
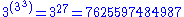not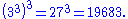 
There is good reason for the choice of this right-to-left order of evaluation. If we used left-to-right evaluation, then
would equal
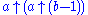, so that 
would not be an essentially new operation.
Right associativity is also natural because we can rewrite the iterated arrow expression
that appears
in the expansion of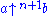
as
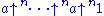, so that all the 
s appear
as left operands of arrow operators. This is significant since the arrow operators are not commutativeCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
.
Writing
for the bth functional power of the function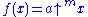 
we have 
.
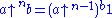The definition could be extrapolated one step, starting with
if n = 0, because exponentiation is repeated multiplication starting with 1. Extrapolating one step more, writing multiplication as repeated addition, is not as straightforward because multiplication is repeated addition starting with 0 instead of 1. "Extrapolating" again one step more, writing addition of n as repeated addition of 1, requires starting with the number a. Compare the definition of the hyper operator, where the starting values for addition and multiplication are also separately specified.
Computing
Computing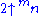
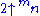can be restated in terms of an infinite table. We place the numbers 
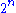in the top row, and fill the left column with values 2. To determine a number in the table, take the number immediately to the left, then look up the required number in the previous row, at the position given by the number just taken.
Values of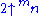 
= hyper(2, m + 2, n) = 2 → n → mConway chained arrow notationConway chained arrow notation, created by mathematician John Horton Conway, is a means of expressing certain extremely large numbers. It is simply a finite sequence of positive integers separated by rightward arrows, e.g. 2 → 3 → 4 → 5 → 6.As with most...m\n 1 2 3 4 5 6 formula 1 2 4 8 16 32 64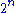 
2 2 4 16 65536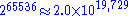 
3 2 4 65536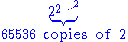 
4 2 4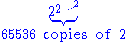 
The table is the same as that of the Ackermann function, except for a shift in
and 
, and an addition of 3 to all values.
Computing
We place the numbers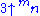
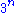in the top row, and fill the left column with values 3. To determine a number in the table, take the number immediately to the left, then look up the required number in the previous row, at the position given by the number just taken.
Values of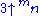 
= hyper(3, m + 2, n) = 3 → n → mConway chained arrow notationConway chained arrow notation, created by mathematician John Horton Conway, is a means of expressing certain extremely large numbers. It is simply a finite sequence of positive integers separated by rightward arrows, e.g. 2 → 3 → 4 → 5 → 6.As with most...m\n 1 2 3 4 5 formula 1 3 9 27 81 243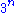 
2 3 27 7,625,597,484,987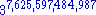 
3 3 7,625,597,484,987 
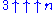
4 3 
Computing
We place the numbers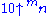
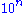in the top row, and fill the left column with values 10. To determine a number in the table, take the number immediately to the left, then look up the required number in the previous row, at the position given by the number just taken.
Values of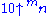 
= hyper(10, m + 2, n) = 10 → n → mConway chained arrow notationConway chained arrow notation, created by mathematician John Horton Conway, is a means of expressing certain extremely large numbers. It is simply a finite sequence of positive integers separated by rightward arrows, e.g. 2 → 3 → 4 → 5 → 6.As with most...m\n 1 2 3 4 5 formula 1 10 100 1,000 10,000 100,000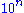 
2 10 10,000,000,000 
3 10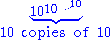 
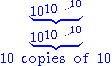
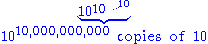
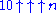
4 10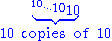 
Note that for 2 ≤ n ≤ 9 the numerical order of the numbers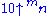
is the lexicographical orderLexicographical orderIn mathematics, the lexicographic or lexicographical order, , is a generalization of the way the alphabetical order of words is based on the alphabetical order of letters.-Definition:Given two partially ordered sets A and B, the lexicographical order on...
with m as the most significant number, so for the numbers of these 8 columns the numerical order is simply line-by-line. The same applies for the numbers in the 97 columns with 3 ≤ n ≤ 99, and if we start from m = 1 even for 3 ≤ n ≤ 9,999,999,999.
Numeration systems based on the hyperoperation sequence
R. L. GoodsteinReuben GoodsteinReuben Louis Goodstein was an English mathematician with a strong interest in the philosophy and teaching of mathematics....
, with a system of notation different from Knuth arrows, used the sequence of hyperoperatorsHyperoperationIn mathematics, the hyperoperation sequenceis an infinite sequence of arithmetic operations that starts with the unary operation of successor, then continues with the binary operations of addition, multiplication and exponentiation, after which the sequence proceeds with further binary operations...
here denoted by
to create systems of numeration for the nonnegative integers. Letting superscripts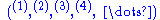 
denote the respective hyperoperators 
, the so-called complete hereditary representation of integer n, at level k and base b, can be expressed as follows using only the first k hyperoperators and using as digits only 0, 1, ..., b-1:
- For 0 ≤ n ≤ b-1, n is represented simply by the corresponding digit.
- For n > b-1, the representation of n is found recursively, first representing n in the form
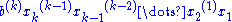
- where xk, ..., x1 are the largest integers satisfying (in turn)
.
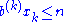
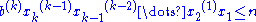- Any xi exceeding b-1 is then re-expressed in the same manner, and so on, repeating this procedure until the resulting form contains only the digits 0, 1, ..., b-1.
The remainder of this section will use
, rather than superscripts, to denote the hyperoperators.
Unnecessary parentheses can be avoided by giving higher-level operators higher precedence in the order of evaluation; thus,
level-1 representations have the form
, with X also of this form;
level-2 representations have the form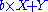
, with X,Y also of this form;
level-3 representations have the form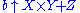
, with X,Y,Z also of this form;
level-4 representations have the form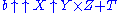
, with X,Y,Z,T also of this form;
and so on.
The representations can be abbreviated by omitting any instances of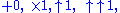
etc.; for example, the level-3 base-2 representation of the number 6 is 
, which abbreviates to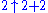 
.
Examples:
The unique base-2 representations of the number 266, at levels 1, 2, 3, 4, and 5 are as follows:
.
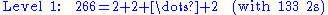
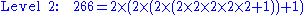
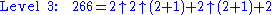
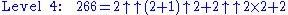
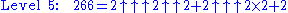See also
- Primitive recursion
- Hyper operator
- Busy beaverBusy beaverIn computability theory, a busy beaver is a Turing machine that attains the maximum "operational busyness" among all the Turing machines in a certain class...
- Cutler's bar notationCutler's bar notationIn mathematics, Cutler's bar notation is a notation system for large numbers, introduced by Mark Cutler in 2004. The idea is based on iterated exponentiation in much the same way that exponentiation is iterated multiplication.-Introduction:...
- Ultra exponential function
- TetrationTetrationIn mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
-