
Knight's tour
Encyclopedia
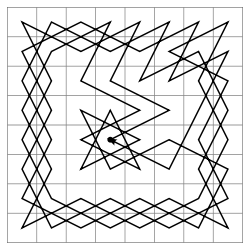
Mathematical chess problem
Mathematical chess problem is a mathematical problem which is formulated using chessboard or chess pieces. These problems belong to recreational mathematics. The most known problems of this kind are Eight queens puzzle or Knight's Tour problems, which have connection to graph theory and combinatorics...
involving a knight
Knight (chess)
The knight is a piece in the game of chess, representing a knight . It is normally represented by a horse's head and neck. Each player starts with two knights, which begin on the row closest to the player, one square from the corner...
on a chessboard
Chessboard
A chessboard is the type of checkerboard used in the board game chess, and consists of 64 squares arranged in two alternating colors...
. The knight is placed on the empty board and, moving according to the rules of chess
Chess
Chess is a two-player board game played on a chessboard, a square-checkered board with 64 squares arranged in an eight-by-eight grid. It is one of the world's most popular games, played by millions of people worldwide at home, in clubs, online, by correspondence, and in tournaments.Each player...
, must visit each square exactly once. A knight's tour is called a closed tour if the knight ends on a square attacking the square from which it began (so that it may tour the board again immediately with the same path). Otherwise the tour is open. The exact number of open tours is still unknown. Creating a program to solve the knight's tour is a common problem given to computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
students. Variations of the knight's tour problem involve chessboards of different sizes than the usual 8 × 8, as well as irregular (non-rectangular) boards.
Theory

Hamiltonian path problem
In the mathematical field of graph theory the Hamiltonian path problem and the Hamiltonian cycle problem are problems of determining whether a Hamiltonian path or a Hamiltonian cycle exists in a given graph . Both problems are NP-complete...
in graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
. The problem of finding a closed knight's tour is similarly an instance of the Hamiltonian cycle problem. Note, however, that unlike the general Hamiltonian path problem
Hamiltonian path problem
In the mathematical field of graph theory the Hamiltonian path problem and the Hamiltonian cycle problem are problems of determining whether a Hamiltonian path or a Hamiltonian cycle exists in a given graph . Both problems are NP-complete...
, the knight's tour problem can be solved in linear time.
History
The earliest known references to the Knight's Tour problem date back to the 9th century AD. The pattern of a knight's tour on a half-board has been presented in verse form (as a literary constraint) in the highly stylized SanskritSanskrit
Sanskrit , is a historical Indo-Aryan language and the primary liturgical language of Hinduism, Jainism and Buddhism.Buddhism: besides Pali, see Buddhist Hybrid Sanskrit Today, it is listed as one of the 22 scheduled languages of India and is an official language of the state of Uttarakhand...
poem Kavyalankara
Kavyalankara
Kavyalankara is the name of two works in Sanskrit poetics :* Kāvyālaṅkāra by Bhamaha , roughly contemporaneous with Daṇḍin...
written by the 9th century India
India
India , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
n poet Rudrata
Rudrata
Rudrata was a Kashmiri poet and literary theorist, who wrote a work called the Kavyalankara in the first quarter of the ninth century. Very little is known about Rudrata...
, which discusses the art of poetry, especially with relation to theater (Natyashastra). As was often the practice in ornate Sanskrit poetry, the syllabic patterns of this poem elucidate a completely different motif, in this case an open knight's tour on a half-chessboard.
One of the first mathematicians to investigate the knight's tour was Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
. The first procedure for completing the Knight's Tour was Warnsdorff's rule, first described in 1823 by H. C. von Warnsdorff.
In the 20th century, the Oulipo
Oulipo
Oulipo is a loose gathering of French-speaking writers and mathematicians which seeks to create works using constrained writing techniques. It was founded in 1960 by Raymond Queneau and François Le Lionnais...
group of writers used it among many others. The most notable example is the Knight's Tour which sets the order of the chapters in Georges Perec
Georges Perec
Georges Perec was a French novelist, filmmaker, documentalist and essayist. He is a member of the Oulipo group...
's novel Life: A User's Manual
Life: A User's Manual
Life A User's Manual is Georges Perec's most famous novel, published in 1978, first translated into English by David Bellos in 1987. Its title page describes it as "novels", in the plural, the reasons for which become apparent on reading...
. The sixth game of the 2010 World Chess Championship between Viswanathan Anand
Viswanathan Anand
V. Anand or Anand Viswanathan, usually referred as Viswanathan Anand, is an Indian chess Grandmaster, the current World Chess Champion, and currently second highest rated player in the world....
and Veselin Topalov
Veselin Topalov
Veselin Aleksandrov Topalov is a Bulgarian chess grandmaster. He currently has the sixth highest rating in the world, and was the challenger facing world champion Viswanathan Anand in the World Chess Championship 2010, losing the match 6½–5½....
saw Anand making 13 consecutive knight moves (albeit using both knights) -– online commentors jested that Anand was trying to solve the Knight's Tour problem during the game.
Closed tours
On an board, there are exactly 26,534,728,821,064 directed closed tours (i.e. two tours along the same path that travel in opposite directions are counted separately, as are rotations and reflections). The number of undirected closed tours is half this number, since every tour can be traced in reverse. There are 9,862 undirected closed tours on a board. No closed tours exist for smaller square boards besides the trivial case (this is a corollaryCorollary
A corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
of the following theorem).
Schwenk's Theorem
For any board with m less than or equal to n, a closed knight's tour is always possible unless one or more of these three conditions are met:- m and n are both odd; m and n are not both 1
- m = 1, 2, or 4; m and n are not both 1
- m = 3 and n = 4, 6, or 8.
Condition 1
One can show that condition 1 prohibits closed tours by a simple argument based on parity and coloring. For the standard black-and-white coloring of the chessboard, the knight must move either from a black square to a white square or from a white square to a black square. Thus in a closed tour the knight must visit the same number of white squares as black squares, and the number of squares visited in total must therefore be even. But if m and n are both odd, the total number of squares is odd. (For example, in a checkerboard there are 13 of one color and 12 of the other.) Therefore closed tours do not exist. Open tours may still exist (with the exception of the trivial case ).Condition 2
Condition 2 states that when the shorter side is of length 1, 2, or 4, no closed tour is possible.When m = 1 or 2, no closed tour is possible because the knight would not be able to reach every square (once again, with the exception of the trivial case ). It can be shown that a board cannot have a closed tour either, by using a coloring argument.
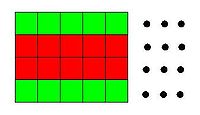
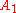 be the set of all squares that would be black and
be the set of all squares that would be black and 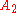 all the squares that would be white, if they were colored according to the alternating black-and-white checkerboard scheme. Consider the figure at right. Define
all the squares that would be white, if they were colored according to the alternating black-and-white checkerboard scheme. Consider the figure at right. Define  to be the set of green squares and
to be the set of green squares and 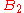 as the set of red squares. There are an equal number of red squares as green squares. Note that from a square in
as the set of red squares. There are an equal number of red squares as green squares. Note that from a square in 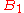 the knight must next jump to a square in
the knight must next jump to a square in 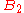 . And since the knight must visit every square once, when the knight is on a square in
. And since the knight must visit every square once, when the knight is on a square in 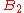 it must move to a square in
it must move to a square in 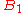 next (otherwise the knight will need to travel to two squares in
next (otherwise the knight will need to travel to two squares in 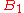 later).
later).If we follow the hypothetical knight's tour, we will find a contradiction.
- The first square the knight goes to will be a square of
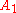 and
and 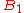 . If it is not, we switch the definitions of
. If it is not, we switch the definitions of  and
and 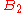 so that it is true.
so that it is true. - The second square must be an element of the sets
 and
and  .
. - The third square must be an element of
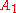 and
and 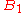 .
. - The fourth square must be an element of the sets
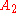 and
and 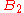 .
. - And so on.
It follows that set
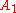 has the same elements as set
has the same elements as set 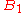 , and set
, and set 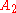 has the same elements as set
has the same elements as set 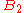 . But this is obviously not true, as the red and green pattern shown above is not the same as a checkerboard pattern; the set of red squares is not the same as the set of black squares (or white, for that matter).
. But this is obviously not true, as the red and green pattern shown above is not the same as a checkerboard pattern; the set of red squares is not the same as the set of black squares (or white, for that matter).So our above assumption was false and there are no closed knight's tours for any board, for any n.
Condition 3
Condition 3 may be proved using casework. Attempting to construct a closed knight's tour on a 3 by 4, 3 by 6, or 3 by 8 will lead to definite failure. 3 by n boards with n even and greater than 8 can be shown to have closed tours by induction (a repeating pattern).All other cases
Simply proving the above three conditions does not prove the theorem. It is still required to prove that all rectangular boards that do not fall in one of the above three categories have closed knight's tours.Computer algorithms
Algorithms other than the simple brute-force searchBrute-force search
In computer science, brute-force search or exhaustive search, also known as generate and test, is a trivial but very general problem-solving technique that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem's...
to find knight's tour solutions are discussed below. It is important to note that an exhaustive brute force approach (one which iterates through all possible move sequences) should never be applied to the Knight's Tour problem (except for very small board sizes). For a regular 8x8 chess board, there are approximately 4×1051 possible move sequences, and it would take an unfathomable amount of time to iterate through such a large number of moves.
Divide and conquer solutions
By dividing the board into smaller pieces, constructing tours on each piece, and patching the pieces together, one can construct tours on most rectangular boards in polynomial time.Neural network solutions

Neural network
The term neural network was traditionally used to refer to a network or circuit of biological neurons. The modern usage of the term often refers to artificial neural networks, which are composed of artificial neurons or nodes...
implementation. The network is set up such that every legal knight's move is represented by a neuron
Artificial neuron
An artificial neuron is a mathematical function conceived as a crude model, or abstraction of biological neurons. Artificial neurons are the constitutive units in an artificial neural network...
, and each neuron is initialized randomly to be either "active" or "inactive" (output of 1 or 0), with 1 implying that the neuron is part of the final solution. Each neuron also has a state function (described below) which is initialized to 0.
When the network is allowed to run, each neuron can change its state and output based on the states and outputs of its neighbors (adjacent knight's moves) according to the following transition rules:
-
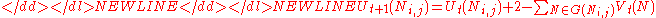
-

where represents discrete intervals of time,
represents discrete intervals of time, 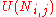 is the state of the neuron connecting square
is the state of the neuron connecting square 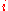 to square
to square 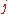 ,
, 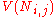 is the output of the neuron from
is the output of the neuron from 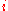 to
to 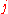 , and
, and 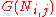 is the set of neighbors of the neuron.
is the set of neighbors of the neuron.
Although divergent cases are possible, the network should eventually converge, which occurs when no neuron changes its state from time to
to  . When the network converges, a solution is found. The solution found by the network will be either a knight's tour, or a series of two or more independent knight's tours within the same board.
. When the network converges, a solution is found. The solution found by the network will be either a knight's tour, or a series of two or more independent knight's tours within the same board.
Warnsdorff's rule
Warnsdorff's rule is a heuristic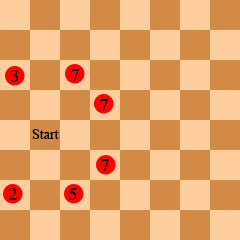 HeuristicHeuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
HeuristicHeuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
method for finding a knight's tour. Briefly, one moves the knight according to the following rule: always proceed to the square from which the knight will have the fewest onward moves. When calculating the number of onward moves for each candidate square, of course, we do not count moves that revisit any square already visited. It is, of course, possible to have two or more choices for which the number of onward moves is equal; there are various methods for breaking such ties, including one devised by Pohl and another by Squirrel and Cull.
This rule may also more generally be applied to any graph. In graph-theoretic terms, each move is made to the adjacent vertex with the least degreeDegree (graph theory)In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
. Although the Hamiltonian path problemHamiltonian path problemIn the mathematical field of graph theory the Hamiltonian path problem and the Hamiltonian cycle problem are problems of determining whether a Hamiltonian path or a Hamiltonian cycle exists in a given graph . Both problems are NP-complete...
is NP-hardNP-hardNP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
in general, on many graphs that occur in practice this heuristic is able to successfully locate a solution in linear time. The knight's tour is a special case.
The heuristicHeuristicHeuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
was first described in "Des Rösselsprungs einfachste und allgemeinste Lösung" by H. C. von Warnsdorff in 1823.
Procedure for Applying the Rule
Warnsdorff’s rule can be applied for any initial position of the knight on the board. All the possible squares which may be reached in one move from this position are located, and the number of moves that the knight would be able to make from each of these squares is found. Then, the rule dictates that the knight move to the square that has the least number of possible following moves. The process is then repeated until each square has been visited.
Some definitions:- A position Q is accessible from a position P if P can move to Q by a single knight's move, and Q has not yet been visited.
- The accessibility of a position P is the number of positions accessible from P.
Procedure:
- set P to be a random initial position on the board
- mark the board at P with the move number "1"
- for each move number from 2 to the number of squares on the board:
- let S be the set of positions accessible from the input position
- set P to be the position in S with minimum accessibility (breaking ties by any preferred method, such as selecting at random)
- mark the board at P with the current move number
- return the marked board – each square will be marked with the move number on which it is visited.
See also
- Abu-Bakr Muhammad ben Yahya as-SuliAbu-Bakr Muhammad ben Yahya as-SuliAbu Bakr Muhammad bin Yahya al-Suli was a nadim of successive Abbasid caliphs. He was noted for his poetry and scholarship and wrote a chronicle called Akhbar al-Radi wa'l-Muttaqi, detailing the reigns of the caliphs al-Radi and al-Muttaqi...
- George KoltanowskiGeorge KoltanowskiGeorge Koltanowski was a Belgian-born American chess player, promoter, and writer. He was informally known as "Kolty". Koltanowski set the world's blindfold record on 20 September 1937, in Edinburgh, by playing 34 chess games simultaneously while blindfolded, making headline news around the world...
- Longest uncrossed knight's pathLongest uncrossed knight's pathThe longest uncrossed knight's path is a mathematical problem involving a knight on the standard 8×8 chessboard or, more generally, on a square n×n board. The problem is to find the longest path the knight can take on the given board, such that the path does not intersect itself...
External links
- Richard W. Henderson, Eugene Roger Apodaca A Knight of Egodeth: Zen Raptured Quietude, 240 Solutions to the Knights Tour in form of Game Book
- Warnsdorff's Rule and its efficiency from Warnsdorff's Rule Web Page
- Knight's tour notes
- Preprint of Pohl's paper (freely accessible)
- SilverKnight - online knight's tour game
- Knightfall - online version of the game as presented by the Riddler.
- warnsdorff.com - Page devoted to Warnsdorff's Rule
Implementations
- The Knight's Tour by Jay Warendorff, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
- An implementation in C#
- Knight's Tours Using a Neural Network Program that creates tours using a neural network, plus gallery of images.
- An interactive version in JavaScript
- Knight's Tour in form of jQuery plugin
-

