
KK-theory
Encyclopedia
In mathematics
, KK-theory is a common generalization both of K-homology
and K-theory
(more precisely operator K-theory
), as an additive bivariant functor on separable C*-algebras. This notion was introduced by the Russian mathematician Gennadi Kasparov in 1980.
It was influenced by Atiyah's concept of Fredholm modules for the Atiyah–Singer index theorem
, and the classification of extensions of C*-algebras by Brown–Douglas–Fillmore (Lawrence G. Brown, Ronald G. Douglas
, Peter Arthur Fillmore 1977). In turn, it has had great success in operator algebraic formalism toward the index theory and the classification of nuclear C*-algebras, as it was the key to the solutions of many problems in operator K-theory
, such as, for instance, the mere calculation of K-groups. Furthermore, it was essential in the development of the Baum–Connes conjecture
and plays a crucial role in noncommutative topology
.
KK-theory was followed by a series of similar bifunctor constructions such as the E-theory and the bivariant periodic cyclic theory, most of them having more category-theoretic flavors, or concerning another class of algebras rather than that of the separable C*-algebras, or incorporating group actions.
Let A and B be separable C*-algebras, where B is also assumed to be σ-unital. The set of cycles is the set of triples (H, ρ, F), where H is a countably generated graded Hilbert module over B, ρ is a *-representation of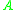 on H as even bounded operators which commute with B, and F is a bounded operator on H of degree 1 which again commutes with B. They are required to fulfill the condition that
on H as even bounded operators which commute with B, and F is a bounded operator on H of degree 1 which again commutes with B. They are required to fulfill the condition that
for a ∈ A are all B-compact operators. A cycle is said to be degenerate if all three expressions are 0 for all .
.
Two cycles are said to be homologous, or homotopic, if there is a cycle between A and IB, where IB denotes the C*-algebra of continuous functions from [0,1] to B, such that there is an even unitary operator from the 0-end of the homotopy to the first cycle, and a unitary operator from the 1-end of the homotopy to the second cycle.
The KK-group KK(A,B) between A and B is then defined to be the set of cycles modulo homotopy. It becomes an abelian group under the direct sum operation of bimodules as the addition, and the class of the degenerate modules as its neutral element.
There are various, but equivalent definitions of the KK-theory, notably the one due to Joachim Cuntz which eliminates bimodule and 'Fredholm' operator F from the picture and puts the accent entirely on the homomorphism ρ. More precisely it can be defined as the set of homotopy classes
of *-homomorphisms from the classifying algebra QA of quasi-homomorphisms to the C*-algebra of compact operators tensored with B. Here, QA is defined as the kernel of the map from the C*-algebraic free product A*A of A with itself to A defined by the identity on both factors.
An important property of KK-theory is the so-called Kasparov product, or the composition product,
which is bilinear with respect to the additive group structures. In particular each element of KK(A, B) gives a homomorphism of K*(A) to K*(B) and another homomorphism K*(B) to K*(A).
The product can be defined much more easily in the Cuntz picture given that there are natural maps from QA to A, and from B to K(H) ⊗ B which induce KK-equivalences.
The composition product gives a new category KK, whose objects are given by the separable C*-algebras while the morphisms between them are given by KK-groups. Moreover, any *-homomorphism of A into B induces an element of KK(A, B) and this correspondence gives a functor from the original category of the separable C*-algebras into KK. The inner automorphisms of the algebras become identity morphisms in KK.
This functor C*-alg → KK is universal among the split-exact, homotopy invariant and stable additive functors on the category of the separable C*-algebras. Any such theory satisfies Bott periodicity in the appropriate sense since KK does.
The Kasparov product can be further generalized to the following form:
It contains as special cases not only the K-theoretic cup product
, but also the K-theoretic cap
, cross, and slant products and the product of extensions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, KK-theory is a common generalization both of K-homology
K-homology
In mathematics, K-homology is a homology theory on the category of compact Hausdorff spaces. It classifies the elliptic pseudo-differential operators acting on the vector bundles over a space...
and K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
(more precisely operator K-theory
Operator K-theory
In mathematics, operator K-theory is a variant of K-theory on the category of Banach algebras ....
), as an additive bivariant functor on separable C*-algebras. This notion was introduced by the Russian mathematician Gennadi Kasparov in 1980.
It was influenced by Atiyah's concept of Fredholm modules for the Atiyah–Singer index theorem
Atiyah–Singer index theorem
In differential geometry, the Atiyah–Singer index theorem, proved by , states that for an elliptic differential operator on a compact manifold, the analytical index is equal to the topological index...
, and the classification of extensions of C*-algebras by Brown–Douglas–Fillmore (Lawrence G. Brown, Ronald G. Douglas
Ronald G. Douglas
Ronald George Douglas is an American mathematician, best known for his work on operator algebras.Douglas was born in Osgood, Indiana. He was an undergraduate at the Illinois Institute of Technology, and received his Ph.D. in 1962 from Louisiana State University as a student of Pasquale Porcelli...
, Peter Arthur Fillmore 1977). In turn, it has had great success in operator algebraic formalism toward the index theory and the classification of nuclear C*-algebras, as it was the key to the solutions of many problems in operator K-theory
Operator K-theory
In mathematics, operator K-theory is a variant of K-theory on the category of Banach algebras ....
, such as, for instance, the mere calculation of K-groups. Furthermore, it was essential in the development of the Baum–Connes conjecture
Baum–Connes conjecture
In mathematics, specifically in operator K-theory, the Baum–Connes conjecture suggests a link between the K-theory of the C*-algebra of a group and the K-homology of the corresponding classifying space of proper actions of that group....
and plays a crucial role in noncommutative topology
Noncommutative topology
Noncommutative topology in mathematics is a term applied to the strictly C*-algebraic part of the noncommutative geometry program. The program has its origins in the Gel'fand duality between the topology of locally compact spaces and the algebraic structure of commutative C*-algebras.Several...
.
KK-theory was followed by a series of similar bifunctor constructions such as the E-theory and the bivariant periodic cyclic theory, most of them having more category-theoretic flavors, or concerning another class of algebras rather than that of the separable C*-algebras, or incorporating group actions.
Definition
The following definition is quite close to the one originally given by Kasparov. This is the form in which most KK-elements arise in applications.Let A and B be separable C*-algebras, where B is also assumed to be σ-unital. The set of cycles is the set of triples (H, ρ, F), where H is a countably generated graded Hilbert module over B, ρ is a *-representation of
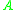 on H as even bounded operators which commute with B, and F is a bounded operator on H of degree 1 which again commutes with B. They are required to fulfill the condition that
on H as even bounded operators which commute with B, and F is a bounded operator on H of degree 1 which again commutes with B. They are required to fulfill the condition that
- [F, ρ(a)], (F^2-1)ρ(a), (F-F^*)ρ(a)
for a ∈ A are all B-compact operators. A cycle is said to be degenerate if all three expressions are 0 for all
 .
.Two cycles are said to be homologous, or homotopic, if there is a cycle between A and IB, where IB denotes the C*-algebra of continuous functions from [0,1] to B, such that there is an even unitary operator from the 0-end of the homotopy to the first cycle, and a unitary operator from the 1-end of the homotopy to the second cycle.
The KK-group KK(A,B) between A and B is then defined to be the set of cycles modulo homotopy. It becomes an abelian group under the direct sum operation of bimodules as the addition, and the class of the degenerate modules as its neutral element.
There are various, but equivalent definitions of the KK-theory, notably the one due to Joachim Cuntz which eliminates bimodule and 'Fredholm' operator F from the picture and puts the accent entirely on the homomorphism ρ. More precisely it can be defined as the set of homotopy classes
- KK(A,B) = [QA, K(H) ⊗ B],
of *-homomorphisms from the classifying algebra QA of quasi-homomorphisms to the C*-algebra of compact operators tensored with B. Here, QA is defined as the kernel of the map from the C*-algebraic free product A*A of A with itself to A defined by the identity on both factors.
Properties
When one takes the C*-algebra C of the complex numbers as the first argument of KK as in KK(C, B) this additive group is naturally isomorphic to the K0-group K0(B) of the second argument B. Similarly when one takes the algebra C0(R) of the continuous functions on the real line decaying at infinity as the first argument, the obtained group KK(C0(R), B) is naturally isomorphic to K1(B).An important property of KK-theory is the so-called Kasparov product, or the composition product,
- KK(A,B) × KK(B,C) → KK(A,C),
which is bilinear with respect to the additive group structures. In particular each element of KK(A, B) gives a homomorphism of K*(A) to K*(B) and another homomorphism K*(B) to K*(A).
The product can be defined much more easily in the Cuntz picture given that there are natural maps from QA to A, and from B to K(H) ⊗ B which induce KK-equivalences.
The composition product gives a new category KK, whose objects are given by the separable C*-algebras while the morphisms between them are given by KK-groups. Moreover, any *-homomorphism of A into B induces an element of KK(A, B) and this correspondence gives a functor from the original category of the separable C*-algebras into KK. The inner automorphisms of the algebras become identity morphisms in KK.
This functor C*-alg → KK is universal among the split-exact, homotopy invariant and stable additive functors on the category of the separable C*-algebras. Any such theory satisfies Bott periodicity in the appropriate sense since KK does.
The Kasparov product can be further generalized to the following form:
- KK(A, B ⊗ E) × KK(B ⊗ D, C) → KK(A ⊗ D, C ⊗ E).
It contains as special cases not only the K-theoretic cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
, but also the K-theoretic cap
Cap product
In algebraic topology the cap product is a method of adjoining a chain of degree p with a cochain of degree q, such that q ≤ p, to form a composite chain of degree p − q. It was introduced by Eduard Čech in 1936, and independently by Hassler Whitney in 1938.-Definition:Let X be a topological...
, cross, and slant products and the product of extensions.

