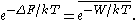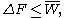Jarzynski equality
Encyclopedia
The Jarzynski equality is an equation
in statistical mechanics
that relates free energy
differences between two equilibrium states and non-equilibrium processes. It is named after the physicist Christopher Jarzynski (then at Los Alamos National Laboratory
) who derived it in 1997.
In thermodynamics
, the free energy difference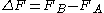
between two states A and B is connected to the work W done on the system through the inequality:
the equality happening only in the case of a quasistatic process
, i.e. when one takes the system from A to B infinitely slowly.
In contrast to the thermodynamic statement above, the JE remains valid no matter how fast the process happens. The equality itself can be straightforwardly derived from the Crooks fluctuation theorem
. The JE states:
Here k is the Boltzmann constant and T is the temperature of the system in the equilibrium state A or, equivalently, the temperature of the heat reservoir
with which the system was thermalized before the process took place.
The over-line indicates an average over all possible realizations of an external process that takes the system from the equilibrium state A to a new, generally nonequilibrium state under the same external conditions as that of the equilibrium state B. (For example, in the textbook case of a gas compressed by a piston, the gas is equilibrated at piston position A and compressed to piston position B; in the Jarzynski equality, the final state of the gas does not need to be equilibrated at this new piston position). In the limit of an infinitely slow process, the work W performed on the system in each realization is numerically the same, so the average becomes irrelevant and the Jarzynski equality reduces to the thermodynamic equality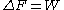
(see above). In general, however, W depends upon the specific initial microstate
of the system, though its average can still be related to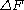
through an application of Jensen's inequality
in the JE, viz.
in accordance with the second law of thermodynamics.
Since its original derivation, the Jarzynski equality has been verified in a variety of contexts, ranging from experiments with biomolecules to numerical simulations. Many other theoretical derivations have also appeared, lending further confidence to its generality.
Another similar statement to the Jarzynski equality is the Nonequilibrium partition identity, which can be traced back to Yamada and Kawasaki. (The Nonequilibrium Partition Identity is the Jarzynski equality applied to two systems whose free energy difference is zero - like straining a fluid.) However, these early statements are very limited in their application. Both Bochkov and Kuzovlev as well as Yamada and Kawasaki consider a deterministic time reversible Hamiltonian system
. As Kawasaki himself noted this precludes any treatment of nonequilibrium steady states. The fact that these nonequilibrium systems heat up forever because of the lack of any thermostatting mechanism leads to divergent integrals etc. No purely Hamiltonian description is capable of treating the experiments carried out to verify the Crooks fluctuation theorem
, Jarzynski equality and the Fluctuation Theorem
. These experiments involve thermostated systems in contact with heat baths.
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
in statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
that relates free energy
Thermodynamic free energy
The thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
differences between two equilibrium states and non-equilibrium processes. It is named after the physicist Christopher Jarzynski (then at Los Alamos National Laboratory
Los Alamos National Laboratory
Los Alamos National Laboratory is a United States Department of Energy national laboratory, managed and operated by Los Alamos National Security , located in Los Alamos, New Mexico...
) who derived it in 1997.
In thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
, the free energy difference
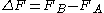between two states A and B is connected to the work W done on the system through the inequality:-
,
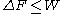the equality happening only in the case of a quasistatic process
Quasistatic process
In thermodynamics, a quasistatic process is a thermodynamic process that happens infinitely slowly. However, it is very important of note that no real process is quasistatic...
, i.e. when one takes the system from A to B infinitely slowly.
In contrast to the thermodynamic statement above, the JE remains valid no matter how fast the process happens. The equality itself can be straightforwardly derived from the Crooks fluctuation theorem
Crooks Fluctuation Theorem
The Crooks equation is an equation in statistical mechanics that relatesthe work done on a system during a non-equilibrium transformation to thefree energy difference between the final and the initial state of the...
. The JE states:
Here k is the Boltzmann constant and T is the temperature of the system in the equilibrium state A or, equivalently, the temperature of the heat reservoir
Heat reservoir
In thermodynamics, a heat reservoir, thermal reservoir, or heat bath is a system whose heat capacity is so large that when it is in thermal contact with some other system of interest its temperature remains effectively constant. The heat bath is effectively an infinite reservoir of energy and...
with which the system was thermalized before the process took place.
The over-line indicates an average over all possible realizations of an external process that takes the system from the equilibrium state A to a new, generally nonequilibrium state under the same external conditions as that of the equilibrium state B. (For example, in the textbook case of a gas compressed by a piston, the gas is equilibrated at piston position A and compressed to piston position B; in the Jarzynski equality, the final state of the gas does not need to be equilibrated at this new piston position). In the limit of an infinitely slow process, the work W performed on the system in each realization is numerically the same, so the average becomes irrelevant and the Jarzynski equality reduces to the thermodynamic equality
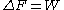(see above). In general, however, W depends upon the specific initial microstateMicrostate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
of the system, though its average can still be related to
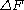through an application of Jensen's inequalityJensen's inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...
in the JE, viz.
in accordance with the second law of thermodynamics.
Since its original derivation, the Jarzynski equality has been verified in a variety of contexts, ranging from experiments with biomolecules to numerical simulations. Many other theoretical derivations have also appeared, lending further confidence to its generality.
History
A question has been raised about who gave the earliest statement of the Jarzynski equality. For example in 1977 the Russian physicists G.N. Bochkov and Yu. E. Kuzovlev (see Bibliography) proposed a generalized version of the Fluctuation-Dissipation relations which holds in the presence of arbitrary external time-dependent forces. Despite its close similarity to the JE, the Bochkov-Kuzovlev result does not relate free energy differences to work measurements, as discussed by Jarzynski himself in 2007 (see references below).Another similar statement to the Jarzynski equality is the Nonequilibrium partition identity, which can be traced back to Yamada and Kawasaki. (The Nonequilibrium Partition Identity is the Jarzynski equality applied to two systems whose free energy difference is zero - like straining a fluid.) However, these early statements are very limited in their application. Both Bochkov and Kuzovlev as well as Yamada and Kawasaki consider a deterministic time reversible Hamiltonian system
Hamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
. As Kawasaki himself noted this precludes any treatment of nonequilibrium steady states. The fact that these nonequilibrium systems heat up forever because of the lack of any thermostatting mechanism leads to divergent integrals etc. No purely Hamiltonian description is capable of treating the experiments carried out to verify the Crooks fluctuation theorem
Crooks Fluctuation Theorem
The Crooks equation is an equation in statistical mechanics that relatesthe work done on a system during a non-equilibrium transformation to thefree energy difference between the final and the initial state of the...
, Jarzynski equality and the Fluctuation Theorem
Fluctuation theorem
The fluctuation theorem , which originated from statistical mechanics, deals with the relative probability that the entropy of a system which is currently away from thermodynamic equilibrium will increase or decrease over a given amount of time...
. These experiments involve thermostated systems in contact with heat baths.
See also
- Fluctuation theoremFluctuation theoremThe fluctuation theorem , which originated from statistical mechanics, deals with the relative probability that the entropy of a system which is currently away from thermodynamic equilibrium will increase or decrease over a given amount of time...
- Provides an equality that quantifies fluctuations in time averaged entropy production in a wide variety of nonequilibrium systems. - Crooks fluctuation theoremCrooks Fluctuation TheoremThe Crooks equation is an equation in statistical mechanics that relatesthe work done on a system during a non-equilibrium transformation to thefree energy difference between the final and the initial state of the...
- Provides a fluctuation theorem between two equilibrium states. Implies Jarzynski equality. - Nonequilibrium partition identity
- Jarzynski Equality on arxiv.org
- "Fluctuation-Dissipation: Response Theory in Statistical Physics" by Umberto Marini Bettolo Marconi, Andrea Puglisi, Lamberto Rondoni, Angelo Vulpiani, http://arxiv.org/abs/0803.0719