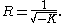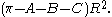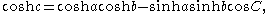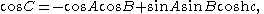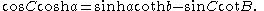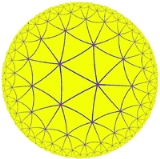
Hyperbolic triangle
Encyclopedia
In mathematics
, the term hyperbolic triangle has more than one meaning.
, a hyperbolic triangle is a figure in the hyperbolic plane, analogous to a triangle in Euclidean geometry, consisting of three sides and three angles. The relations among the angles and sides are analogous to those of spherical trigonometry
; they are most conveniently stated if the lengths are measured in terms of a special unit of length analogous to a radian
. In terms of the Gaussian curvature
K of the plane this unit is given by
In all the trig formulas stated below the sides a, b, and c must be measured in this unit. In a hyperbolic triangle the sum of the angles A, B, C (respectively opposite to the side with the corresponding letter) is strictly less than a straight angle. The difference is often called the defect
of the triangle. The area of a hyperbolic triangle is equal to its defect multiplied by the square of R:
The corresponding theorem in spherical geometry
is Girard's theorem first proven by Johann Heinrich Lambert
.
The hyperbolic sine, cosine, and tangent are hyperbolic functions which are analogous to the standard trigonometric functions.
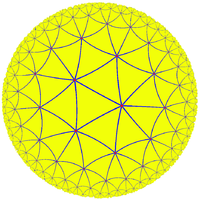
There is a law of cosines:
its dual:
a law of sines:
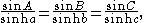
and a four-parts formula:
, they meet at an ideal vertex on the circle at infinity. If all three are vertices are ideal, then the resulting figure is called an ideal triangle
. An ideal hyperbolic triangle has an angle sum of 0°, a property it has in common with the triangular area in the Euclidean plane bounded by three tangent circles.
s sinh, cosh and tanh, a hyperbolic triangle is a right triangle
in the first quadrant of the Cartesian plane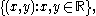
with one vertex
at the origin, base on the diagonal ray y = x, and third vertex on the hyperbola
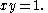
The length of the base of such a triangle is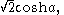
and the altitude
is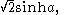
where a is the appropriate hyperbolic angle
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the term hyperbolic triangle has more than one meaning.

Hyperbolic geometry
In hyperbolic geometryHyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, a hyperbolic triangle is a figure in the hyperbolic plane, analogous to a triangle in Euclidean geometry, consisting of three sides and three angles. The relations among the angles and sides are analogous to those of spherical trigonometry
Spherical trigonometry
Spherical trigonometry is a branch of spherical geometry which deals with polygons on the sphere and the relationships between the sides and the angles...
; they are most conveniently stated if the lengths are measured in terms of a special unit of length analogous to a radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
. In terms of the Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
K of the plane this unit is given by
In all the trig formulas stated below the sides a, b, and c must be measured in this unit. In a hyperbolic triangle the sum of the angles A, B, C (respectively opposite to the side with the corresponding letter) is strictly less than a straight angle. The difference is often called the defect
Defect (geometry)
In geometry, the defect means the failure of some angles to add up to the expected amount of 360° or 180°, when such angles in the plane would...
of the triangle. The area of a hyperbolic triangle is equal to its defect multiplied by the square of R:
The corresponding theorem in spherical geometry
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
is Girard's theorem first proven by Johann Heinrich Lambert
Johann Heinrich Lambert
Johann Heinrich Lambert was a Swiss mathematician, physicist, philosopher and astronomer.Asteroid 187 Lamberta was named in his honour.-Biography:...
.
Right triangles
If C is a right angle then:- The sine of angle A is the ratio of the hyperbolic sine of the side opposite the angle to the hyperbolic sine of the hypotenuseHypotenuseIn geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
.
-
-

- The cosine of angle A is the ratio of the hyperbolic tangent of the adjacent leg to the hyperbolic tangent of the hypotenuse.
-

- The tangent of angle A is the ratio of the hyperbolic tangent of the opposite leg to the hyperbolic sine of the adjacent leg.
-

-
The hyperbolic sine, cosine, and tangent are hyperbolic functions which are analogous to the standard trigonometric functions.
Oblique triangles
Whether C is a right angle or not, the following relationships hold.There is a law of cosines:
its dual:
a law of sines:
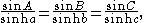
and a four-parts formula:
Ideal triangles
If a pair of sides is asymptotic they may be said to form an angle of zero. In projective geometryProjective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, they meet at an ideal vertex on the circle at infinity. If all three are vertices are ideal, then the resulting figure is called an ideal triangle
Ideal triangle
In hyperbolic geometry an ideal triangle is a hyperbolic triangle whose three vertices all lie on the circle at infinity. In the hyperbolic metric, any two ideal triangles are congruent...
. An ideal hyperbolic triangle has an angle sum of 0°, a property it has in common with the triangular area in the Euclidean plane bounded by three tangent circles.
Euclidean geometry
In the foundations of the hyperbolic functionHyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
s sinh, cosh and tanh, a hyperbolic triangle is a right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
in the first quadrant of the Cartesian plane
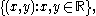
with one vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
at the origin, base on the diagonal ray y = x, and third vertex on the hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
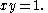
The length of the base of such a triangle is
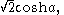
and the altitude
Altitude (triangle)
In geometry, an altitude of a triangle is a straight line through a vertex and perpendicular to a line containing the base . This line containing the opposite side is called the extended base of the altitude. The intersection between the extended base and the altitude is called the foot of the...
is
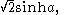
where a is the appropriate hyperbolic angle
Hyperbolic angle
In mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...
.