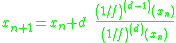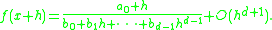Householder's method
Encyclopedia
In numerical analysis
, the class of Householder
's methods are root-finding algorithm
s used for functions of one real variable with continuous derivatives up to some order d+1, where d will be the order of the Householder's method.
The algorithm is iterative and it has rate of convergence
of d+1.
beginning with an initial guess x0.
If f is a (d+1) times continuously differentiable function and a is a zero of f but not of its derivative, then, in a neighborhood of a, the iterates xn satisfy:
, for some 
This means that the iterates converge to the zero if the initial guess is sufficiently close, and that the convergence has rate (d+1).
-valued, continuously
differentiable
function f(x) have a simple zero at x=a, that is a root f(a)=0 of multiplicity one, which is equivalent to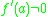
. Then 1/f(x) has a singularity that simple pole (also of multiplicity one) at a, and close to a the behavior of 1/f(x) is dominated by the factor 1/(x-a). Approximatively one gets
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, the class of Householder
Alston Scott Householder
Alston Scott Householder was an American mathematician who specialized in mathematical biology and numerical analysis, inventor of the Householder transformation and of Householder's method...
's methods are root-finding algorithm
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
s used for functions of one real variable with continuous derivatives up to some order d+1, where d will be the order of the Householder's method.
The algorithm is iterative and it has rate of convergence
Rate of convergence
In numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
of d+1.
Method
Like any root-finding method, the Householder's method is a numerical algorithm for solving the nonlinear equation f(x) = 0. In this case, the function f has to be a function of one real variable. The method consists of a sequence of iterations:
beginning with an initial guess x0.
If f is a (d+1) times continuously differentiable function and a is a zero of f but not of its derivative, then, in a neighborhood of a, the iterates xn satisfy:
, for some This means that the iterates converge to the zero if the initial guess is sufficiently close, and that the convergence has rate (d+1).
Motivation
An approximate idea of the origin of the Householder's method derives from the geometric series. Let the realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued, continuously
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
differentiable
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
function f(x) have a simple zero at x=a, that is a root f(a)=0 of multiplicity one, which is equivalent to
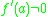. Then 1/f(x) has a singularity that simple pole (also of multiplicity one) at a, and close to a the behavior of 1/f(x) is dominated by the factor 1/(x-a). Approximatively one gets
-
-
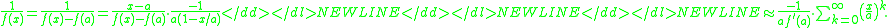
Here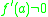
because a is a simple zero of f(x). The coefficient of degree d has the value 
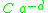. Thus, one can now reconstruct the zero a by dividing the coefficient of degree d-1 by the coefficient of degree d. Since this geometric series is an approximation to the Taylor expansion of 1/f(x), one can get estimates of the zero of f(x) − now without prior knowledge of the location of this zero − by dividing the corresponding coefficients of the Taylor expansion of 1/f(x) or, more generally, 1/f(b+x). From that one gets, for any integer d, and if the corresponding derivatives exist,
-
-
The methods of lower order
The Householder's method of order 1 is just Newton's methodNewton's methodIn numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
, since:-
-
For the Householder's method of order 2 one gets Halley's methodHalley's methodIn numerical analysis, Halley’s method is a root-finding algorithm used for functions of one real variable with a continuous second derivative, i.e., C2 functions. It is named after its inventor Edmond Halley, who also discovered Halley's Comet....
, since the identities-
-
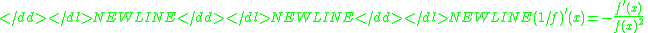
and-
-
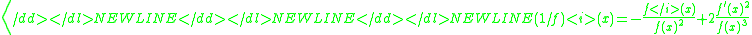
result in-
-
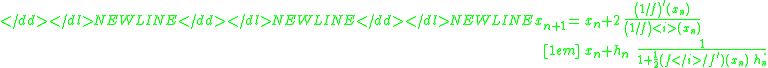
In the last line,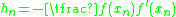
is the update of the Newton iteration at the point 
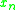. This line was added to demonstrate where the difference to the simple Newton's method lies.
The third order method is obtained from the identity of the third order derivative of 1/f-
-
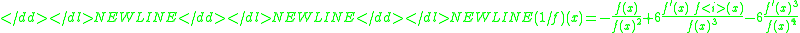
and has the formula-
-
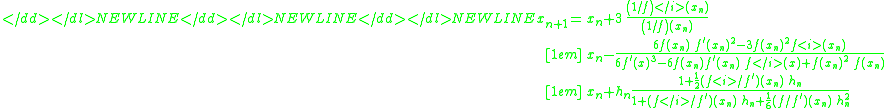
and so on...
Example
The first problem solved by Newton with the Newton-Raphson-Simpson method was the polynomial equation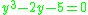
. He observed that there should be a solution close to 2. Replacing y=x+2 transforms the equation into
-
-
.
-
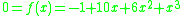The Taylor series of the reciprocal function starts with-
-
The result of applying Householder's methods of various orders at x=0 is also obtained by dividing neighboring coefficients of the latter power series. For the first orders one gets the following values after just one iteration step: For an example, in the case of the 3rd order,
.
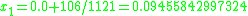d x1 1 0.10000000000000000000000000000000 2 0.094339622641509433962264150943396 3 0.094558429973238180196253345227476 4 0.094551282051282051282051282051282 5 0.094551486538216154140615031261963 6 0.094551481438752142436492263099119 7 0.094551481543746895938379484125813 8 0.094551481542336756233561913325371 9 0.094551481542324837086869382419375 10 0.094551481542326678478801765822985
As one can see, there are a little bit more than d correct decimal places for each order d.
Let's calculate the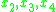
values for some lowest order,
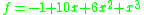
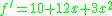
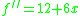
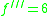
And using following relations,
- 1st order;
- 2nd order;
- 3rd order;
x 1st (Newton) 2nd (Halley) 3rd order 4th order x1 0.1 0.09433962264151 0.09455842997324 0.09455128205128 x2 0.09456812110419 0.09455148154016421472 0.094551481542326591482567 x3 0.09455148169819930297 0.09455148154232659148238654 0.09455148154232659148238654057931 x4 0.09455148154232659149606485 0.0945514815423265914823865405793 0.09455148154232659148238654057931 x5 0.09455148154232659148238654057931 0.0945514815423265914823865405793 x6 0.09455148154232659148238654057931
Derivation
An exact derivation of the Householder's methods starts from the Padé approximation of order (d+1) of the function resp. its Taylor development, where the approximant with linear numerator is chosen. If this has been achieved, the update for the next approximation results from computing the unique zero of the numerator.
The Padé approximation has the form
The rational function has a zero at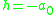
.
Just as the Taylor polynomial of degree d has d+1 coefficients that depend on the function f, also the Padé approximation always has d+1 coefficients dependent on f and its derivatives. More precisely, in any Pade approximant, the degrees of numerator and denominator polynomials have to add to the order of the approximant. Therefore,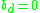
has to hold.
One could determine the Padé approximant starting from the Taylor polynomial of f using Euclid's algorithm. However, starting from the Taylor polynomial of 1/f is shorter and leads directly to the given formula. Since-
-
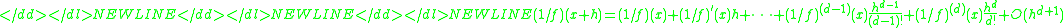
has to be equal to the inverse of the desired rational function, we get after multiplying with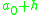
in the power 
the equation
-
-
.
-
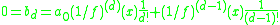Now, solving the last equation for the zero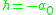
of the numerator results in
-
-
.
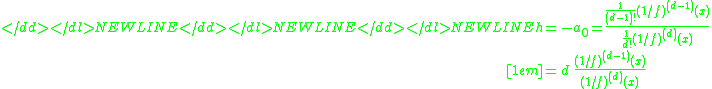This implies the iteration formula-
-
.
-
-
-
-
-
-
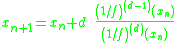- 1st order;
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
