Set of regular n-gonal hosohedrons
Example hexagonal hosohedron on a sphere
Type	Regular polyhedron Regular polyhedron A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags... or spherical tiling
Faces	n digon Digon In geometry, a digon is a polygon with two sides and two vertices. It is degenerate in a Euclidean space, but may be non-degenerate in a spherical space.A digon must be regular because its two edges are the same length... s
Edges	n
Vertices	2
Schläfli symbol	{2,n}
Vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...	2n
Coxeter–Dynkin diagram
Wythoff symbol Wythoff symbol In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....	n | 2 2
Symmetry group	Dnh, [2,n], (*22n)
Dual polyhedron Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...	dihedron Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, an n-gonal

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

 hosohedron is a tessellation of lune

Lune (mathematics)

In geometry, a lune is either of two figures, both shaped roughly like a crescent Moon. The word "lune" derives from luna, the Latin word for Moon.-Plane geometry:...

s on a spherical surface, such that each lune shares the same two vertices. A regular n-gonal hosohedron has Schläfli symbol {2, n}.

Hosohedrons as regular polyhedrons

For a regular polyhedron whose Schläfli symbol is {m, n}, the number of polygonal faces may be found by: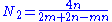


The platonic solid

Platonic solid

In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...

s known to antiquity are the only integer solutions for m ≥ 3 and n ≥ 3. The restriction m ≥ 3 enforces that the polygonal faces must have at least three sides.

When considering polyhedrons as a spherical tiling, this restriction may be relaxed, since digons can be represented as spherical lunes, having non-zero area. Allowing m = 2 admits a new infinite class of regular polyhedrons, which are the hosohedrons. On a spherical surface, the polyhedron {2, n} is represented as n abutting lunes, with interior angles of 2π/n. All these lunes share two common vertices.

A regular trigonal hosohedron, represented as a tessellation of 3 spherical lunes on a sphere.

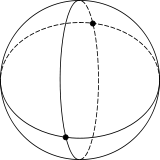A regular tetragonal hosohedron, represented as a tessellation of 4 spherical lunes on a sphere.

Relationship with Steinmetz Solid

The tetragonal hosohedron is topologically equivalent to the bicylinder Steinmetz solid, the intersection of two cylinders at right-angles.

Derivative polyhedrons

The dual

Dual polyhedron

In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...

 of the n-gonal hosohedron {2, n} is the n-gonal dihedron

Dihedron

A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...

, {n, 2}. The polyhedron {2,2} is self-dual, and is both a hosohedron and a dihedron.

A hosohedron may be modified in the same manner as the other polyhedrons to produce a truncated variation. The truncated n-gonal hosohedron is the n-gonal prism

Prism (geometry)

In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...

.

Hosotopes

Multidimensional

Dimension

In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...

 analogues in general are called hosotopes. A regular hosotope with Schläfli symbol {2,p,...,q} has two vertices, each with a vertex figure

Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

 {p,...,q}.

The two-dimensional hosotope {2} is a digon

Digon

In geometry, a digon is a polygon with two sides and two vertices. It is degenerate in a Euclidean space, but may be non-degenerate in a spherical space.A digon must be regular because its two edges are the same length...

.

Etymology

The prefix “hoso-” was invented by H.S.M. Coxeter

Harold Scott MacDonald Coxeter

Harold Scott MacDonald "Donald" Coxeter, was a British-born Canadian geometer. Coxeter is regarded as one of the great geometers of the 20th century. He was born in London but spent most of his life in Canada....

, and possibly derives from the English “hose”.