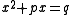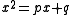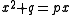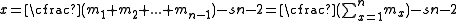History of algebra
Encyclopedia
Algebra
is a branch of mathematics
concerning the study of structure, relation
, and quantity
. Elementary algebra
is the branch that deals with solving for the operands of arithmetic
equations. Modern or abstract algebra
has its origins as an abstraction of elementary algebra. Some historians believe that the earliest mathematical research was done by the priest classes of ancient civilizations, such as the Babylonia
ns, to go along with religious rituals. The origins of algebra can thus be traced back to ancient Babylonian mathematicians
roughly four thousand years ago.
word Al-Jabr, and this comes from the treatise written in 820 by the medieval Persian mathematician, , entitled, in Arabic, كتاب الجبر والمقابلة or , which can be translated as The Compendious Book on Calculation by Completion and Balancing. The treatise provided for the systematic solution of linear
and quadratic equation
s. Although the exact meaning of the word al-jabr is still unknown, most historians agree that the word meant something like "restoration", "completion", "reuniter of broken bones" or "bonesetter." The term is used by al-Khwarizmi to describe the operations that he introduced, "reduction
" and "balancing", referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation.
As important as the symbolism, or lack thereof, that was used in algebra was the degree of the equations that were used. Quadratic equations played an important role in early algebra; and throughout most of history, until the early modern period, all quadratic equations were classified as belonging to one of three categories.
where p and q are positive.
This trichotomy comes about because quadratic equations of the form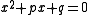
, with p and q positive, have no positive roots.
In between the rhetorical and syncopated stages of symbolic algebra, a geometric constructive algebra was developed by classical Greek
and Vedic Indian mathematicians
in which algebraic equations were solved through geometry. For instance, an equation of the form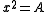
was solved by finding the side of a square of area A.
The origins of algebra can be traced to the ancient Babylonians
, who developed a positional number system that greatly aided them in solving their rhetorical algebraic equations. The Babylonians were not interested in exact solutions but approximations, and so they would commonly use linear interpolation
to approximate intermediate values. One of the most famous tablets is the Plimpton 322 tablet
, created around 1900–1600 BCE, which gives a table of Pythagorean triples and represents some of the most advanced mathematics prior to Greek mathematics.
Babylonian algebra was much more advanced than the Egyptian algebra of the time; whereas the Egyptians were mainly concerned with linear equations the Babylonians were more concerned with quadratic and cubic equations. The Babylonians had developed flexible algebraic operations with which they were able to add equals to equals and multiply both sides of an equation by like quantities so as to eliminate fractions and factors. They were familiar with many simple forms of factoring, three-term quadratic equations with positive roots, and many cubic equations although it is not known if they were able to reduce the general cubic equation.
.png)
Ancient Egyptian algebra dealt mainly with linear equations while the Babylonians found these equations too elementary and developed mathematics to a higher level than the Egyptians.
The Rhind Papyrus, also known as the Ahmes Papyrus, is an ancient Egyptian papyrus written circa 1650 BCE by Ahmes, who transcribed it from an earlier work that he dated to between 2000 and 1800 BCE. It is the most extensive ancient Egyptian mathematical document known to historians. The Rhind Papyrus contains problems where linear equations of the form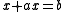
and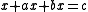 
are solved, where a, b, and c are known and x, which is referred to as "aha" or heap, is the unknown. The solutions were possibly, but not likely, arrived at by using the "method of false position," or regula falsi, where first a specific value is substituted into the left hand side of the equation, then the required arithmetic calculations are done, thirdly the result is compared to the right hand side of the equation, and finally the correct answer is found through the use of proportions. In some of the problems the author "checks" his solution, thereby writing one of the earliest known simple proofs.
had no algebra, but this is inaccurate. By the time of Plato
, Greek mathematics had undergone a drastic change. The Greeks created a geometric algebra where terms were represented by sides of geometric objects, usually lines, that had letters associated with them, and with this new form of algebra they were able to find solutions to equations by using a process that they invented, known as "the application of areas". "The application of areas" is only a part of geometric algebra and it is thoroughly covered in Euclid's Elements.
An example of geometric algebra would be solving the linear equation ax = bc. The ancient Greeks would solve this equation by looking at it as an equality of areas rather than as an equality between the ratios a:b and c:x. The Greeks would construct a rectangle with sides of length b and c, then extend a side of the rectangle to length a, and finally they would complete the extended rectangle so as to find the side of the rectangle that is the solution.
(ca. 400 BCE – ca. 350 BCE) worked with simultaneous linear equations. In particular, he created the then famous rule that was known as the "bloom of Thymaridas" or as the "flower of Thymaridas", which states that:
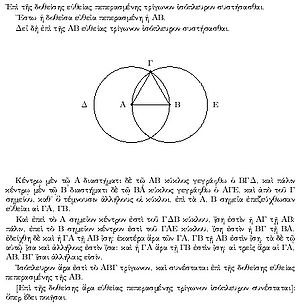or using modern notion, the solution of the following system of n linear equations in n unknowns,
is,
Iamblichus goes on to describe how some systems of linear equations that are not in this form can be placed into this form.
Euclid
(Greek
: ) was a Greek
mathematician who flourished in Alexandria
, Egypt
, almost certainly during the reign of Ptolemy I (323
–283 BC
E). Neither the year nor place of his birth have been established, nor the circumstances of his death.
Euclid is regarded as the "father of geometry
". His Elements
is the most successful textbook
in the history of mathematics
. Although he is one of the most famous mathematicians in history there are no new discoveries attributed to him, rather he is remembered for his great explanatory skills. The Elements is not, as is sometimes thought, a collection of all Greek mathematical knowledge to its date, rather, it is an elementary introduction to it.
Elements, provided the framework for generalizing formulae beyond the solution of particular problems into more general systems of stating and solving equations.
Book II of the Elements contains fourteen propositions, which in Euclid's time were extremely significant for doing geometric algebra. These propositions and their results are the geometric equivalents of our modern symbolic algebra and trigonometry. Today, using modern symbolic algebra, we let symbols represent known and unknown magnitudes (i.e. numbers) and then apply algebraic operations on them. While in Euclid's time magnitudes were viewed as line segments and then results were deduced using the axioms or theorems of geometry.
Many basic laws of addition and multiplication are included or proved geometrically in the Elements. For instance, proposition 1 of Book II states:
But this is nothing more than the geometric version of the (left) distributive law,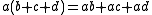
; and in Books V and VII of the Elements the commutative and associative laws for multiplication are demonstrated.
Many basic equations were also proved geometrically. For instance, proposition 5 in Book II proves that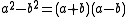
, and proposition 4 in Book II proves that 
.
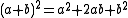Furthermore, there are also geometric solutions given to many equations. For instance, proposition 6 of Book II gives the solution to the quadratic equation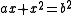
, and proposition 11 of Book II gives a solution to 
.
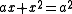is a work written by Euclid for use at the schools of Alexandria and it was meant to be used as a companion volume to the first six books of the Elements. The book contains some fifteen definitions and ninety-five statements, of which there are about two dozen statements that serve as algebraic rules or formulas. Some of these statements are geometric equivalents to solutions of quadratic equations. For instance, Data contains the solutions to the equations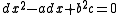
and the familiar Babylonian equation 
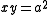, x ± y = b.
is a curve that results from the intersection of a cone with a plane. There are three primary types of conic sections: ellipse
s (including circles), parabolas, and hyperbolas. The conic sections are reputed to have been discovered by Menaechmus
(ca. 380 BCE – ca, 320 BCE) and since dealing with conic sections is equivalent to dealing with their respective equations, they played geometric roles equivalent to cubic equations and other higher order equations.
Menaechmus knew that in a parabola, the equation y2 = lx holds, where l is a constant called the latus rectum, although he was not aware of the fact that any equation in two unknowns determines a curve. He apparently derived these properties of conic sections and others as well. Using this information it was now possible to find a solution to the problem of the duplication of the cube by solving for the points at which two parabolas intersect, a solution equivalent to solving a cubic equation.
We are informed by Eutocius that the method he used to solve the cubic equation was due to Dionysodorus
(250 BCE – 190 BCE). Dionysodorus solved the cubic by means of the intersection of a rectangular hyperbola
and a parabola
. This was related to a problem in Archimedes
' On the Sphere and Cylinder. Conic sections would be studied and used for thousands of years by Greek, and later Islamic and European, mathematicians. In particular Apollonius of Perga
's famous Conics deals with conic sections, among other topics.
E with the Chou Pei Suan Ching
, generally considered to be one of the oldest Chinese mathematical documents.
, written around 250 BC
E, is one of the most influential of all Chinese math books and it is composed of some 246 problems. Chapter eight deals with solving determinate and indeterminate simultaneous linear equations using positive and negative numbers, with one problem dealing with solving four equations in five unknowns.
(or Li Ye) (1192 – 1272 CE). He used fan fa, or Horner's method, to solve equations of degree as high as six, although he did not describe his method of solving equations.
, was written by the wealthy governor and minister Ch'in Chiu-shao
(ca. 1202 – ca. 1261 CE) and with the invention of a method of solving simultaneous congruences, it marks the high point in Chinese indeterminate analysis.
The earliest known magic squares appeared in China. In Nine Chapters the author solves a system of simultaneous linear equations by placing the coefficients and constant terms of the linear equations into a magic square (i.e. a matrix) and performing column reducing operations on the magic square. The earliest known magic squares of order greater than three are attributed to Yang Hui
(fl. ca. 1261 – 1275), who worked with magic squares of order as high as ten.
, called heaven, earth, man and matter, represented the four unknown quantities in his algebraic equations. The Ssy-yüan yü-chien deals with simultaneous equations and with equations of degrees as high as fourteen. The author uses the method of fan fa, today called Horner's method
, to solve these equations.
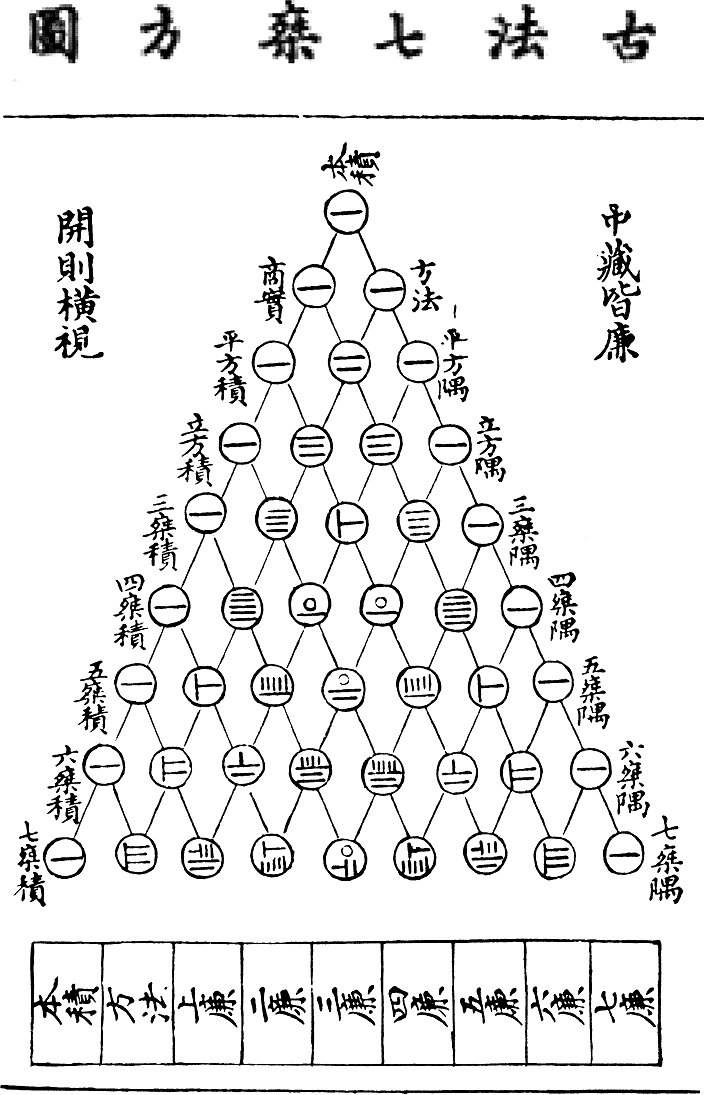
The Precious Mirror opens with a diagram of the arithmetic triangle (Pascal's triangle) using a round zero symbol, but Chu Shih-chieh denies credit for it. A similar triangle appears in Yang Hui's work, but without the zero symbol.
There are many summation series equations given without proof in the Precious mirror. A few of the summation series are:
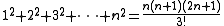
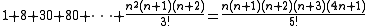
Diophantus
was a Hellenistic
mathematician who lived circa 250 CE, but the uncertainty of this date is so great that it may be off by more than a century. He is known for having written Arithmetica, a treatise that was originally thirteen books but of which only the first six have survived. Arithmetica has very little in common with traditional Greek mathematics since it is divorced from geometric methods, and it is different from Babylonian mathematics in that Diophantus is concerned primarily with exact solutions, both determinate and indeterminate, instead of simple approximations.
In Arithmetica, Diophantus is the first to use symbols for unknown numbers as well as abbreviations for powers of numbers, relationships, and operations; thus he used what is now known as syncopated algebra. The main difference between Diophantine syncopated algebra and modern algebraic notation is that the former lacked special symbols for operations, relations, and exponentials. So, for example, what we would write as
Diophantus would have written this as
where the symbols represent the following:
Note that the coefficients come after the variables and that addition is represented by the juxtaposition of terms. A literal symbol-for-symbol translation of Diophantus's syncopated equation into a modern symbolic equation would be the following:
and, to clarify, if the modern parentheses and plus are used then the above equation can be rewritten as:
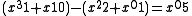
Arithmetica is a collection of some 150 solved problems with specific numbers and there is no postulational development nor is a general method explicitly explained, although generality of method may have been intended and there is no attempt to find all of the solutions to the equations. Arithmetica does contain solved problems involving several unknown quantities, which are solved, if possible, by expressing the unknown quantities in terms of only one of them. Arithmetica also makes use of the identities:
documents are dated to around the middle of the first millennium BCE (around the 6th century BCE).
The recurring themes in Indian mathematics are, among others, determinate and indeterminate linear and quadratic equations, simple mensuration, and Pythagorean triples.
(476–550 CE) was an Indian mathematician who authored Aryabhatiya
. In it he gave the rules,
and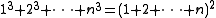
(fl. 628) was an Indian mathematician who authored Brahma Sphuta Siddhanta. In his work Brahmagupta solves the general quadratic equation for both positive and negative roots. In indeterminate analysis Brahmagupta gives the Pythagorean triads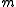
, 
, 
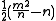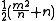, but this is a modified form of an old Babylonian rule that Brahmagupta may have been familiar with. He was the first to give a general solution to the linear Diophantine equation ax + by = c, where a, b, and c are integers. Unlike Diophantus who only gave one solution to an indeterminate equation, Brahmagupta gave all integer solutions; but that Brahmagupta used some of the same examples as Diophantus has led some historians to consider the possibility of a Greek influence on Brahmagupta's work, or at least a common Babylonian source.
Like the algebra of Diophantus, the algebra of Brahmagupta was syncopated. Addition was indicated by placing the numbers side by side, subtraction by placing a dot over the subtrahend, and division by placing the divisor below the dividend, similar to our notation but without the bar. Multiplication, evolution, and unknown quantities were represented by abbreviations of appropriate terms. The extent of Greek influence on this syncopation
, if any, is not known and it is possible that both Greek and Indian syncopation may be derived from a common Babylonian source.
and Vija-Ganita, which contain problems dealing with determinate and indeterminate linear and quadratic equations, and Pythagorean triples and he fails to distinguish between exact and approximate statements. Many of the problems in Lilavati and Vija-Ganita are derived from other Hindu sources, and so Bhaskara is at his best in dealing with indeterminate analysis.
Bhaskara uses the initial symbols of the names for colors as the symbols of unknown variables. So, for example, what we would write today as
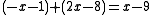
Bhaskara would have written as
where ya indicates the first syllable of the word for black, and ru is taken from the word species. The dots over the numbers indicate subtraction.
ic Arab Empire
saw almost no scientific or mathematical achievements since the Arabs, with their newly conquered empire, had not yet gained any intellectual drive and research in other parts of the world had faded. In the second half of the 8th century, Islam had a cultural awakening, and research in mathematics and the sciences increased. The Muslim Abbasid
caliph
al-Mamun (809–833) is said to have had a dream where Aristotle appeared to him, and as a consequence al-Mamun ordered that Arabic translation be made of as many Greek works as possible, including Ptolemy's Almagest and Euclid's Elements. Greek works would be given to the Muslims by the Byzantine Empire
in exchange for treaties, as the two empires held an uneasy peace. Many of these Greek works were translated by Thabit ibn Qurra
(826–901), who translated books written by Euclid, Archimedes, Apollonius, Ptolemy, and Eutocius.
There are three theories about the origins of Arabic Algebra. The first emphasizes Hindu influence, the second emphasizes Mesopotamian or Persian-Syriac influence and the third emphasizes Greek influence. Many scholars believe that it is the result of a combination of all three sources.
Throughout their time in power, before the fall of Islamic civilization, the Arabs used a fully rhetorical algebra, where often even the numbers were spelled out in words. The Arabs would eventually replace spelled out numbers (e.g. twenty-two) with Arabic numerals
(e.g. 22), but the Arabs never adopted or developed a syncopated or symbolic algebra, until the work of Ibn al-Banna
in the 13th century and Abū al-Hasan ibn Alī al-Qalasādī
in the 15th century.
" (Bait al-Hikma) in Baghdad, which was established by Al-Mamun. Al-Khwarizmi, who died around 850 CE, wrote more than half a dozen mathematical and astronomical works; some of which were based on the Indian Sindhind. One of al-Khwarizmi's most famous books is entitled Al-jabr wa'l muqabalah or The Compendious Book on Calculation by Completion and Balancing
, and it gives an exhaustive account of solving polynomials up to the second degree. The book also introduced the fundamental concept of "reduction
" and "balancing", referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation. This is the operation which Al-Khwarizmi originally described as al-jabr.
R. Rashed and Angela Armstrong write:
Al-Jabr is divided into six chapters, each of which deals with a different type of formula. The first chapter of Al-Jabr deals with equations whose squares equal its roots (ax2 = bx), the second chapter deals with squares equal to number (ax2 = c), the third chapter deals with roots equal to a number (bx = c), the fourth chapter deals with squares and roots equal a number (ax2 + bx = c), the fifth chapter deals with squares and number equal roots (ax2 + c = bx), and the sixth and final chapter deals with roots and number equal to squares (bx + c = ax2).
In Al-Jabr, al-Khwarizmi uses geometric proofs, he does not recognize the root x = 0, and he only deals with positive roots. He also recognizes that the discriminant
must be positive and described the method of completing the square
, though he does not justify the procedure. The Greek influence is shown by Al-Jabrs geometric foundations and by one problem taken from Heron. He makes use of lettered diagrams but all of the coefficients in all of his equations are specific numbers since he had no way of expressing with parameters what he could express geometrically; although generality of method is intended.
Al-Khwarizmi most likely did not know of Diophantus's Arithmetica, which became known to the Arabs sometime before the 10th century. And even though al-Khwarizmi most likely knew of Brahmagupta's work, Al-Jabr is fully rhetorical with the numbers even being spelled out in words. So, for example, what we would write as
Diophantus would have written as
And al-Khwarizmi would have written as
authored a manuscript entitled Logical Necessities in Mixed Equations, which is very similar to al-Khwarzimi's Al-Jabr and was published at around the same time as, or even possibly earlier than, Al-Jabr. The manuscript gives exactly the same geometric demonstration as is found in Al-Jabr, and in one case the same example as found in Al-Jabr, and even goes beyond Al-Jabr by giving a geometric proof that if the discriminant is negative then the quadratic equation has no solution. The similarity between these two works has led some historians to conclude that Arabic algebra may have been well developed by the time of al-Khwarizmi and 'Abd al-Hamid.
s as algebra
ic objects. The Egypt
ian mathematician Abū Kāmil Shujā ibn Aslam (c. 850–930) was the first to accept irrational numbers (often in the form of a square root
, cube root or fourth root
) as solutions to quadratic equation
s or as coefficient
s in an equation
. He was also the first to solve three non-linear simultaneous equations
with three unknown variables
.
Al-Karkhi
(953–1029), also known as Al-Karaji, was the successor of Abū al-Wafā' al-Būzjānī (940–998) and he discovered the first numerical solution to equations of the form ax2n + bxn = c. Al-Karkhi only considered positive roots. Al-Karkhi is also regarded as the first person to free algebra from geometrical
operations and replace them with the type of arithmetic
operations which are at the core of algebra today. His work on algebra and polynomial
s, gave the rules for arithmetic operations to manipulate polynomials. The historian of mathematics
F. Woepcke, in Extrait du Fakhri, traité d'Algèbre par Abou Bekr Mohammed Ben Alhacan Alkarkhi (Paris
, 1853), praised Al-Karaji for being "the first who introduced the theory of algebraic calculus
". Stemming from this, Al-Karaji investigated binomial coefficients and Pascal's triangle
.
(ca. 1050–1123) wrote a book on Algebra that went beyond Al-Jabr to include equations of the third degree. Omar Khayyám provided both arithmetic and geometric solutions for quadratic equations, but he only gave geometric solutions for general cubic equations
since he mistakenly believed that arithmetic solutions were impossible. His method of solving cubic equations by using intersecting conics had been used by Menaechmus
, Archimedes
, and Ibn al-Haytham (Alhazen), but Omar Khayyám generalized the method to cover all cubic equations with positive roots. He only considered positive roots and he did not go past the third degree. He also saw a strong relationship between Geometry and Algebra.
In the 12th century, Sharaf al-Dīn al-Tūsī (1135–1213) wrote the Al-Mu'adalat (Treatise on Equations), which dealt with eight types of cubic equations with positive solutions and five types of cubic equations which may not have positive solutions. He used what would later be known as the "Ruffini
-Horner
method" to numerically
approximate the root of a cubic equation. He also developed the concepts of the maxima and minima
of curves in order to solve cubic equations which may not have positive solutions. He understood the importance of the discriminant
of the cubic equation and used an early version of Cardano
's formula to find algebraic solutions to certain types of cubic equations. Some scholars, such as Roshdi Rashed, argue that Sharaf al-Din discovered the derivative
of cubic polynomials and realized its significance, while other scholars connect his solution to the ideas of Euclid and Archimedes.
Sharaf al-Din also developed the concept of a function
. In his analysis of
the equation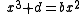
for example, he begins by changing the equation's form to 
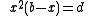. He then states that the question of whether the equation has a solution depends on whether or not the “function” on the left side reaches the value 
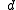. To determine this, he finds a maximum value for the function. He proves that the maximum value occurs when 
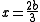, which gives the functional value 
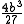. Sharaf al-Din then states that if this value is less than 
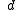, there are no positive solutions; if it is equal to 
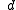, then there is one solution at 
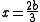; and if it is greater than 
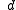, then there are two solutions, one between 
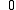and 
and 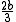one between 
and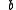 
.
In the early 15th century, Jamshīd al-Kāshī
developed an early form of Newton's method
to numerically solve the equation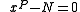
to find roots of 
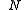. Al-Kāshī also developed decimal fractions and claimed to have discovered it himself. However, J. Lennart Berggrenn notes that he was mistaken, as decimal fractions were first used five centuries before him by the Baghdad
i mathematician Abu'l-Hasan al-Uqlidisi
as early as the 10th century.
specializing in Islamic inheritance jurisprudence
during the 12th century, developed the modern symbolic mathematical notation
for fractions
, where the numerator and denominator are separated by a horizontal bar. This same fractional notation appeared soon after in the work of Fibonacci
in the 13th century.
Abū al-Hasan ibn Alī al-Qalasādī
(1412–1482) was the last major medieval Arab
algebraist, who made the first attempt at creating an algebraic notation
since Ibn al-Banna
two centuries earlier, who was himself the first to make such an attempt since Diophantus
and Brahmagupta
in ancient times. The syncopated notations of his predecessors, however, lacked symbols for mathematical operations
. Al-Qalasadi "took the first steps toward the introduction of algebraic symbolism by using letters in place of numbers" and by "using short Arabic words, or just their initial letters, as mathematical symbols."
as a mathematical center, so does the death of Boethius signal the end of mathematics in the Western Roman Empire
. Although there was some work being done at Athens
, it came to a close when in 529
the Byzantine
emperor Justinian closed the pagan philosophical schools. The year 529
is now taken to be the beginning of the medieval period. Scholars fled the West towards the more hospitable East, particularly towards Persia, where they found haven under King Chosroes
and established what might be termed an "Athenian Academy in Exile". Under a treaty with Justinian, Chosroes would eventually return the scholars to the Eastern Empire. During the Dark Ages, European mathematics was at its nadir with mathematical research consisting mainly of commentaries on ancient treatises; and most of this research was centered in the Byzantine Empire
. The end of the medieval period is set as the fall of Constantinople
to the Turks
in 1453.
and by the 13th century, European mathematics was beginning to rival the mathematics of other lands. In the 13th century, the solution of a cubic equation by Fibonacci
is representative of the beginning of a revival in European algebra.
As the Islamic world was declining after the 15th century, the European world was ascending. And it is here that Algebra was further developed.
was developed by Japanese mathematician
Kowa Seki in the 17th century, followed by Gottfried Leibniz
ten years later, for the purpose of solving systems of simultaneous linear equations using matrices
. Gabriel Cramer
also did some work on matrices and determinants in the 18th century.
The symbol
commonly denotes an unknown variable
. Even though any letter can be used,
is the most common choice. This usage can be traced back to the Arabic
word šay' شيء = “thing,” used in Arabic algebra texts such as the Al-Jabr
, and was taken into Old Spanish
with the pronunciation “šei,” which was written xei, and was soon habitually abbreviated to
. (The Spanish
pronunciation
of “x” has changed since). Some sources say that this
is an abbreviation of Latin
causa, which was a translation of Arabic شيء. This started the habit of using letters to represent quantities in algebra
. In mathematics, an “italicized
x” (
) is often used to avoid potential confusion with the multiplication symbol.
was implicit in trigonometric and logarithmic tables, which existed in his day, Gottfried Leibniz
was the first, in 1692 and 1694, to employ it explicitly, to denote any of several geometric concepts derived from a curve, such as abscissa
, ordinate
, tangent
, chord
, and the perpendicular. In the 18th century, "function" lost these geometrical associations.
Leibniz realized that the coefficients of a system of linear equation
s could be arranged into an array, now called a matrix
, which can be manipulated to find the solution of the system, if any. This method was later called Gaussian elimination
. Leibniz also discovered Boolean algebra and symbolic logic, also relevant to algebra.
was developed in the 19th century, initially focusing on what is now called Galois theory
, and on constructibility
issues.
mathematician Diophantus
has traditionally been known as "the father of algebra" but debate now exists as to whether or not Al-Khwarizmi
deserves this title instead. Those who support Diophantus point to the fact that the algebra found in Al-Jabr
is more elementary than the algebra found in Arithmetica
and that Arithmetica is syncopated while Al-Jabr is fully rhetorical.
Those who support Al-Khwarizmi point to the fact that he gave an exhaustive explanation for the algebraic solution of quadratic equations with positive roots, and was the first to teach algebra in an elementary form
and for its own sake, whereas Diophantus was primarily concerned with the theory of numbers
. Al-Khwarizmi also introduced the fundamental concept of "reduction" and "balancing" (which he originally used the term al-jabr to refer to), referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation. Other supporters of Al-Khwarizmi point to his algebra no longer being concerned "with a series of problem
s to be resolved, but an exposition
which starts with primitive terms in which the combinations must give all possible prototypes for equations, which henceforward explicitly constitute the true object of study." They also point to his treatment of an equation for its own sake and "in a generic manner, insofar as it does not simply emerge in the course of solving a problem, but is specifically called on to define an infinite class of problems." Al-Khwarizmi's work established algebra as a mathematical discipline that is independent of geometry
and arithmetic
.
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
is a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
concerning the study of structure, relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
, and quantity
Quantity
Quantity is a property that can exist as a magnitude or multitude. Quantities can be compared in terms of "more" or "less" or "equal", or by assigning a numerical value in terms of a unit of measurement. Quantity is among the basic classes of things along with quality, substance, change, and relation...
. Elementary algebra
Elementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
is the branch that deals with solving for the operands of arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
equations. Modern or abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
has its origins as an abstraction of elementary algebra. Some historians believe that the earliest mathematical research was done by the priest classes of ancient civilizations, such as the Babylonia
Babylonia
Babylonia was an ancient cultural region in central-southern Mesopotamia , with Babylon as its capital. Babylonia emerged as a major power when Hammurabi Babylonia was an ancient cultural region in central-southern Mesopotamia (present-day Iraq), with Babylon as its capital. Babylonia emerged as...
ns, to go along with religious rituals. The origins of algebra can thus be traced back to ancient Babylonian mathematicians
Babylonian mathematics
Babylonian mathematics refers to any mathematics of the people of Mesopotamia, from the days of the early Sumerians to the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited...
roughly four thousand years ago.
Etymology
The word "algebra" is derived from the ArabicArabic language
Arabic is a name applied to the descendants of the Classical Arabic language of the 6th century AD, used most prominently in the Quran, the Islamic Holy Book...
word Al-Jabr, and this comes from the treatise written in 820 by the medieval Persian mathematician, , entitled, in Arabic, كتاب الجبر والمقابلة or , which can be translated as The Compendious Book on Calculation by Completion and Balancing. The treatise provided for the systematic solution of linear
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
and quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
s. Although the exact meaning of the word al-jabr is still unknown, most historians agree that the word meant something like "restoration", "completion", "reuniter of broken bones" or "bonesetter." The term is used by al-Khwarizmi to describe the operations that he introduced, "reduction
Reduction (mathematics)
In mathematics, reduction refers to the rewriting of an expression into a simpler form. For example, the process of rewriting a fraction into one with the smallest whole-number denominator possible is called "reducing a fraction"...
" and "balancing", referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation.
Algebraic expression
Algebra did not always make use of the symbolism that is now ubiquitous in mathematics, rather, it went through three distinct stages. The stages in the development of symbolic algebra are roughly as follows:- Rhetorical algebra, where equations are written in full sentences. For example, the rhetorical form of x + 1 = 2 is "The thing plus one equals two" or possibly "The thing plus 1 equals 2". Rhetorical algebra was first developed by the ancient Babylonians and remained dominant up to the 16th century.
- Syncopated algebra, where some symbolism is used but which does not contain all of the characteristic of symbolic algebra. For instance, there may be a restriction that subtraction may be used only once within one side of an equation, which is not the case with symbolic algebra. Syncopated algebraic expression first appeared in DiophantusDiophantusDiophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
' ArithmeticaArithmeticaArithmetica is an ancient Greek text on mathematics written by the mathematician Diophantus in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate equations and indeterminate equations.Equations in the book are called Diophantine equations...
, followed by BrahmaguptaBrahmaguptaBrahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
's Brahma Sphuta Siddhanta. - Symbolic algebra, where full symbolism is used. Early steps toward this can be seen in the work of several Islamic mathematiciansIslamic mathematicsIn the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
such as Ibn al-Banna and al-QalasadiAbu al-Hasan ibn Ali al-QalasadiAbū al-Ḥasan ibn ʿAlī ibn Muḥammad ibn ʿAlī al-Qalaṣādī was a Muslim mathematician from Al-Andalus specializing in Islamic inheritance jurisprudence...
, though fully symbolic algebra sees its culmination in the work of René DescartesRené DescartesRené Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
.
As important as the symbolism, or lack thereof, that was used in algebra was the degree of the equations that were used. Quadratic equations played an important role in early algebra; and throughout most of history, until the early modern period, all quadratic equations were classified as belonging to one of three categories.
where p and q are positive.
This trichotomy comes about because quadratic equations of the form
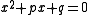, with p and q positive, have no positive roots.In between the rhetorical and syncopated stages of symbolic algebra, a geometric constructive algebra was developed by classical Greek
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
and Vedic Indian mathematicians
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
in which algebraic equations were solved through geometry. For instance, an equation of the form
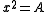was solved by finding the side of a square of area A.Conceptual stages
In addition to the three stages of expressing algebraic ideas, there were four conceptual stages in the development of algebra that occurred alongside the changes in expression. These four stages were as follows:- Geometric stage, where the concepts of algebra are largely geometricGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
. This dates back to the BabyloniansBabylonian mathematicsBabylonian mathematics refers to any mathematics of the people of Mesopotamia, from the days of the early Sumerians to the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited...
and continued with the GreeksGreek mathematicsGreek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
, and was later revived by Omar KhayyámOmar KhayyámOmar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....
. - Static equation-solving stage, where the objective is to find numbers satisfying certain relationships. The move away from geometric algebra dates back to DiophantusDiophantusDiophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
and BrahmaguptaBrahmaguptaBrahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
, but algebra didn't decisively move to the static equation-solving stage until Al-KhwarizmiMuhammad ibn Musa al-Khwarizmi'There is some confusion in the literature on whether al-Khwārizmī's full name is ' or '. Ibn Khaldun notes in his encyclopedic work: "The first who wrote upon this branch was Abu ʿAbdallah al-Khowarizmi, after whom came Abu Kamil Shojaʿ ibn Aslam." . 'There is some confusion in the literature on...
's Al-JabrThe Compendious Book on Calculation by Completion and Balancing, also known under a shorter name spelled as Hisab al-jabr w’al-muqabala, Kitab al-Jabr wa-l-Muqabala and other transliterations) is a mathematical book written in Arabic in approximately AD 820 by the Persian (Arabic for "The Compendious Book on Calculation by Completion and Balancing", in...
. - Dynamic function stage, where motion is an underlying idea. The idea of a functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
began emerging with Sharaf al-Dīn al-Tūsī, but algebra didn't decisively move to the dynamic function stage until Gottfried LeibnizGottfried LeibnizGottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
. - Abstract stage, where mathematical structure plays a central role. Abstract algebraAbstract algebraAbstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
is largely a product of the 19th and 20th centuries.
Babylonian algebra
Babylonian mathematics
Babylonian mathematics refers to any mathematics of the people of Mesopotamia, from the days of the early Sumerians to the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited...
, who developed a positional number system that greatly aided them in solving their rhetorical algebraic equations. The Babylonians were not interested in exact solutions but approximations, and so they would commonly use linear interpolation
Linear interpolation
Linear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
to approximate intermediate values. One of the most famous tablets is the Plimpton 322 tablet
Plimpton 322
Plimpton 322 is a Babylonian clay tablet, notable as containing an example of Babylonian mathematics. It has number 322 in the G.A. Plimpton Collection at Columbia University...
, created around 1900–1600 BCE, which gives a table of Pythagorean triples and represents some of the most advanced mathematics prior to Greek mathematics.
Babylonian algebra was much more advanced than the Egyptian algebra of the time; whereas the Egyptians were mainly concerned with linear equations the Babylonians were more concerned with quadratic and cubic equations. The Babylonians had developed flexible algebraic operations with which they were able to add equals to equals and multiply both sides of an equation by like quantities so as to eliminate fractions and factors. They were familiar with many simple forms of factoring, three-term quadratic equations with positive roots, and many cubic equations although it is not known if they were able to reduce the general cubic equation.
Egyptian algebra
Ancient Egyptian algebra dealt mainly with linear equations while the Babylonians found these equations too elementary and developed mathematics to a higher level than the Egyptians.
The Rhind Papyrus, also known as the Ahmes Papyrus, is an ancient Egyptian papyrus written circa 1650 BCE by Ahmes, who transcribed it from an earlier work that he dated to between 2000 and 1800 BCE. It is the most extensive ancient Egyptian mathematical document known to historians. The Rhind Papyrus contains problems where linear equations of the form
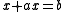and 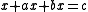are solved, where a, b, and c are known and x, which is referred to as "aha" or heap, is the unknown. The solutions were possibly, but not likely, arrived at by using the "method of false position," or regula falsi, where first a specific value is substituted into the left hand side of the equation, then the required arithmetic calculations are done, thirdly the result is compared to the right hand side of the equation, and finally the correct answer is found through the use of proportions. In some of the problems the author "checks" his solution, thereby writing one of the earliest known simple proofs.Greek geometric algebra
It is sometimes alleged that the GreeksGreeks
The Greeks, also known as the Hellenes , are a nation and ethnic group native to Greece, Cyprus and neighboring regions. They also form a significant diaspora, with Greek communities established around the world....
had no algebra, but this is inaccurate. By the time of Plato
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
, Greek mathematics had undergone a drastic change. The Greeks created a geometric algebra where terms were represented by sides of geometric objects, usually lines, that had letters associated with them, and with this new form of algebra they were able to find solutions to equations by using a process that they invented, known as "the application of areas". "The application of areas" is only a part of geometric algebra and it is thoroughly covered in Euclid's Elements.
An example of geometric algebra would be solving the linear equation ax = bc. The ancient Greeks would solve this equation by looking at it as an equality of areas rather than as an equality between the ratios a:b and c:x. The Greeks would construct a rectangle with sides of length b and c, then extend a side of the rectangle to length a, and finally they would complete the extended rectangle so as to find the side of the rectangle that is the solution.
Bloom of Thymaridas
Iamblichus in Introductio arithmatica tells us that ThymaridasThymaridas
Thymaridas of Paros was an ancient Greek mathematician and Pythagorean noted for his work on prime numbers and simultaneous linear equations.- Life and work :...
(ca. 400 BCE – ca. 350 BCE) worked with simultaneous linear equations. In particular, he created the then famous rule that was known as the "bloom of Thymaridas" or as the "flower of Thymaridas", which states that:
If the sum of n quantities be given, and also the sum of every pair containing a particular quantity, then this particular quantity is equal to 1/ (n - 2) of the difference between the sums of these pairs and the first given sum.
x + x1 + x2 + ... + xn-1 = s
x + x1 = m1
x + x2 = m2
.
.
.
x + xn-1 = mn-1
is,
Iamblichus goes on to describe how some systems of linear equations that are not in this form can be placed into this form.
Euclid of Alexandria
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
(Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
: ) was a Greek
Greeks
The Greeks, also known as the Hellenes , are a nation and ethnic group native to Greece, Cyprus and neighboring regions. They also form a significant diaspora, with Greek communities established around the world....
mathematician who flourished in Alexandria
Alexandria
Alexandria is the second-largest city of Egypt, with a population of 4.1 million, extending about along the coast of the Mediterranean Sea in the north central part of the country; it is also the largest city lying directly on the Mediterranean coast. It is Egypt's largest seaport, serving...
, Egypt
Egypt
Egypt , officially the Arab Republic of Egypt, Arabic: , is a country mainly in North Africa, with the Sinai Peninsula forming a land bridge in Southwest Asia. Egypt is thus a transcontinental country, and a major power in Africa, the Mediterranean Basin, the Middle East and the Muslim world...
, almost certainly during the reign of Ptolemy I (323
323 BC
Year 323 BC was a year of the pre-Julian Roman calendar. At the time, it was known as the Year of the Consulship of Longus and Cerretanus...
–283 BC
283 BC
Year 283 BC was a year of the pre-Julian Roman calendar. At the time it was known as the Year of the Consulship of Dolabella and Maximus...
E). Neither the year nor place of his birth have been established, nor the circumstances of his death.
Euclid is regarded as the "father of geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
". His Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
is the most successful textbook
Textbook
A textbook or coursebook is a manual of instruction in any branch of study. Textbooks are produced according to the demands of educational institutions...
in the history of mathematics
History of mathematics
The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past....
. Although he is one of the most famous mathematicians in history there are no new discoveries attributed to him, rather he is remembered for his great explanatory skills. The Elements is not, as is sometimes thought, a collection of all Greek mathematical knowledge to its date, rather, it is an elementary introduction to it.
Elements
The geometric work of the Greeks, typified in Euclid'sEuclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
Elements, provided the framework for generalizing formulae beyond the solution of particular problems into more general systems of stating and solving equations.
Book II of the Elements contains fourteen propositions, which in Euclid's time were extremely significant for doing geometric algebra. These propositions and their results are the geometric equivalents of our modern symbolic algebra and trigonometry. Today, using modern symbolic algebra, we let symbols represent known and unknown magnitudes (i.e. numbers) and then apply algebraic operations on them. While in Euclid's time magnitudes were viewed as line segments and then results were deduced using the axioms or theorems of geometry.
Many basic laws of addition and multiplication are included or proved geometrically in the Elements. For instance, proposition 1 of Book II states:
- If there be two straight lines, and one of them be cut into any number of segments whatever, the rectangle contained by the two straight lines is equal to the rectangles contained by the uncut straight line and each of the segments.
But this is nothing more than the geometric version of the (left) distributive law,
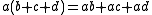; and in Books V and VII of the Elements the commutative and associative laws for multiplication are demonstrated.Many basic equations were also proved geometrically. For instance, proposition 5 in Book II proves that
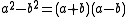, and proposition 4 in Book II proves that 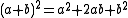.Furthermore, there are also geometric solutions given to many equations. For instance, proposition 6 of Book II gives the solution to the quadratic equation
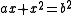, and proposition 11 of Book II gives a solution to 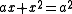.Data
DataData (Euclid)
Data is a work by Euclid. It deals with the nature and implications of "given" information in geometrical problems. The subject matter is closely related to the first four books of Euclid's Elements....
is a work written by Euclid for use at the schools of Alexandria and it was meant to be used as a companion volume to the first six books of the Elements. The book contains some fifteen definitions and ninety-five statements, of which there are about two dozen statements that serve as algebraic rules or formulas. Some of these statements are geometric equivalents to solutions of quadratic equations. For instance, Data contains the solutions to the equations
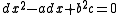and the familiar Babylonian equation 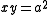, x ± y = b.Conic sections
A conic sectionConic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
is a curve that results from the intersection of a cone with a plane. There are three primary types of conic sections: ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s (including circles), parabolas, and hyperbolas. The conic sections are reputed to have been discovered by Menaechmus
Menaechmus
Menaechmus was an ancient Greek mathematician and geometer born in Alopeconnesus in the Thracian Chersonese, who was known for his friendship with the renowned philosopher Plato and for his apparent discovery of conic sections and his solution to the then-long-standing problem of doubling the cube...
(ca. 380 BCE – ca, 320 BCE) and since dealing with conic sections is equivalent to dealing with their respective equations, they played geometric roles equivalent to cubic equations and other higher order equations.
Menaechmus knew that in a parabola, the equation y2 = lx holds, where l is a constant called the latus rectum, although he was not aware of the fact that any equation in two unknowns determines a curve. He apparently derived these properties of conic sections and others as well. Using this information it was now possible to find a solution to the problem of the duplication of the cube by solving for the points at which two parabolas intersect, a solution equivalent to solving a cubic equation.
We are informed by Eutocius that the method he used to solve the cubic equation was due to Dionysodorus
Dionysodorus
Dionysodorus of Caunus was an ancient Greek mathematician.- Life and work :Little is known about the life of Dionysodorus...
(250 BCE – 190 BCE). Dionysodorus solved the cubic by means of the intersection of a rectangular hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
and a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. This was related to a problem in Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
' On the Sphere and Cylinder. Conic sections would be studied and used for thousands of years by Greek, and later Islamic and European, mathematicians. In particular Apollonius of Perga
Apollonius of Perga
Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
's famous Conics deals with conic sections, among other topics.
Chinese algebra
Chinese Mathematics dates to at least 300 BC300 BC
Year 300 BC was a year of the pre-Julian Roman calendar. At the time it was known as the Year of the Consulship of Corvus and Pansa...
E with the Chou Pei Suan Ching
Chou Pei Suan Ching
The Zhou Bi Suan Jing, or Chou Pei Suan Ching, is one of the oldest and most famous Chinese mathematical texts. The title literally means The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven....
, generally considered to be one of the oldest Chinese mathematical documents.
Nine Chapters on the Mathematical Art
Chiu-chang suan-shu or The Nine Chapters on the Mathematical ArtThe Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
, written around 250 BC
250 BC
Year 250 BC was a year of the pre-Julian Roman calendar. At the time it was known as the Year of the Consulship of Regulus and Longus...
E, is one of the most influential of all Chinese math books and it is composed of some 246 problems. Chapter eight deals with solving determinate and indeterminate simultaneous linear equations using positive and negative numbers, with one problem dealing with solving four equations in five unknowns.
Sea-Mirror of the Circle Measurements
Ts'e-yuan hai-ching, or Sea-Mirror of the Circle Measurements, is a collection of some 170 problems written by Li ZhiLi Zhi (mathematician)
Li Zhi , later Li Ye , was a Chinese mathematician and scholar, who published and improved the tian yuan shu method for solving polynomial equations of one variable.- Name :...
(or Li Ye) (1192 – 1272 CE). He used fan fa, or Horner's method, to solve equations of degree as high as six, although he did not describe his method of solving equations.
Mathematical Treatise in Nine Sections
Shu-shu chiu-chang, or Mathematical Treatise in Nine SectionsMathematical Treatise in Nine Sections
The Mathematical Treatise in Nine Sections is a mathematical text written by Chinese Southern Song dynasty mathematician Qin Jiushao in the year 1247.This book contains nine chapters:#Da Yan type ;#Heaven phenomena...
, was written by the wealthy governor and minister Ch'in Chiu-shao
Ch'in Chiu-Shao
Qin Jiushao , courtesy name Daogu , was a Chinese mathematician.- Biography :He was born in Ziyang, Sichuan, his ancestry was from Shandong, and is now regarded as one of the greatest mathematicians of the 13th century. This is particularly remarkable, as Qin did not devote his life to mathematics...
(ca. 1202 – ca. 1261 CE) and with the invention of a method of solving simultaneous congruences, it marks the high point in Chinese indeterminate analysis.
Magic squares
Yang Hui
Yang Hui , courtesy name Qianguang , was a Chinese mathematician from Qiantang , Zhejiang province during the late Song Dynasty . Yang worked on magic squares, magic circles and the binomial theorem, and is best known for his contribution of presenting 'Yang Hui's Triangle'...
(fl. ca. 1261 – 1275), who worked with magic squares of order as high as ten.
Precious Mirror of the Four Elements
Ssy-yüan yü-chien《四元玉鑒》, or Precious Mirror of the Four Elements, was written by Chu Shih-chieh in 1303 and it marks the peak in the development of Chinese algebra. The four elementsFour elements
Four elements may refer to:* Classical elements, such as air, fire, earth and water* 4 Elements, an album by Chronic Future* Group 4 element, one of the chemical elements in Group 4 of the periodic table...
, called heaven, earth, man and matter, represented the four unknown quantities in his algebraic equations. The Ssy-yüan yü-chien deals with simultaneous equations and with equations of degrees as high as fourteen. The author uses the method of fan fa, today called Horner's method
Horner scheme
In numerical analysis, the Horner scheme , named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation...
, to solve these equations.
The Precious Mirror opens with a diagram of the arithmetic triangle (Pascal's triangle) using a round zero symbol, but Chu Shih-chieh denies credit for it. A similar triangle appears in Yang Hui's work, but without the zero symbol.
There are many summation series equations given without proof in the Precious mirror. A few of the summation series are:
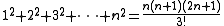
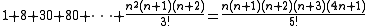
Diophantine algebra
Diophantus
Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
was a Hellenistic
Hellenistic civilization
Hellenistic civilization represents the zenith of Greek influence in the ancient world from 323 BCE to about 146 BCE...
mathematician who lived circa 250 CE, but the uncertainty of this date is so great that it may be off by more than a century. He is known for having written Arithmetica, a treatise that was originally thirteen books but of which only the first six have survived. Arithmetica has very little in common with traditional Greek mathematics since it is divorced from geometric methods, and it is different from Babylonian mathematics in that Diophantus is concerned primarily with exact solutions, both determinate and indeterminate, instead of simple approximations.
In Arithmetica, Diophantus is the first to use symbols for unknown numbers as well as abbreviations for powers of numbers, relationships, and operations; thus he used what is now known as syncopated algebra. The main difference between Diophantine syncopated algebra and modern algebraic notation is that the former lacked special symbols for operations, relations, and exponentials. So, for example, what we would write as
Diophantus would have written this as
where the symbols represent the following:
| Symbol | Representation |
|---|---|
| represents 1 | |
| represents 2 | |
| represents 5 | |
| represents 10 | |
| ς | represents the unknown quantity (i.e. the variable) |
| (short for ) represents "equals" | |
| represents the subtraction of everything that follows it up to | |
| Μ | represents the zeroth power of the variable (i.e. a constant term) |
| ΔΥ | represents the second power of the variable, from Greek , meaning strength or power |
| ΚΥ | represents the third power of the variable, from Greek , meaning a cube |
| ΔΥΔ | represents the fourth power of the variable |
| ΔΚΥ | represents the fifth power of the variable |
| ΚΥΚ | represents the sixth power of the variable |
Note that the coefficients come after the variables and that addition is represented by the juxtaposition of terms. A literal symbol-for-symbol translation of Diophantus's syncopated equation into a modern symbolic equation would be the following:
and, to clarify, if the modern parentheses and plus are used then the above equation can be rewritten as:
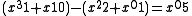
Arithmetica is a collection of some 150 solved problems with specific numbers and there is no postulational development nor is a general method explicitly explained, although generality of method may have been intended and there is no attempt to find all of the solutions to the equations. Arithmetica does contain solved problems involving several unknown quantities, which are solved, if possible, by expressing the unknown quantities in terms of only one of them. Arithmetica also makes use of the identities:
 |
 |
 |
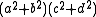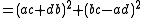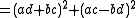Indian algebra
The method known as "Modus Indorum" or the method of the Indians have become our algebra today. This algebra came along with the Hindu Number system to Arabia and then migrated to Europe. The earliest known Indian mathematicalIndian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
documents are dated to around the middle of the first millennium BCE (around the 6th century BCE).
The recurring themes in Indian mathematics are, among others, determinate and indeterminate linear and quadratic equations, simple mensuration, and Pythagorean triples.
Aryabhata
AryabhataAryabhata
Aryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
(476–550 CE) was an Indian mathematician who authored Aryabhatiya
Aryabhatiya
Āryabhaṭīya or Āryabhaṭīyaṃ, a Sanskrit astronomical treatise, is the magnum opus and only extant work of the 5th century Indian mathematician, Āryabhaṭa.- Structure and style:...
. In it he gave the rules,
and
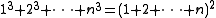
Brahma Sphuta Siddhanta
BrahmaguptaBrahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
(fl. 628) was an Indian mathematician who authored Brahma Sphuta Siddhanta. In his work Brahmagupta solves the general quadratic equation for both positive and negative roots. In indeterminate analysis Brahmagupta gives the Pythagorean triads
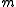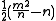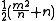, , , but this is a modified form of an old Babylonian rule that Brahmagupta may have been familiar with. He was the first to give a general solution to the linear Diophantine equation ax + by = c, where a, b, and c are integers. Unlike Diophantus who only gave one solution to an indeterminate equation, Brahmagupta gave all integer solutions; but that Brahmagupta used some of the same examples as Diophantus has led some historians to consider the possibility of a Greek influence on Brahmagupta's work, or at least a common Babylonian source.Like the algebra of Diophantus, the algebra of Brahmagupta was syncopated. Addition was indicated by placing the numbers side by side, subtraction by placing a dot over the subtrahend, and division by placing the divisor below the dividend, similar to our notation but without the bar. Multiplication, evolution, and unknown quantities were represented by abbreviations of appropriate terms. The extent of Greek influence on this syncopation
History of algebra
Algebra is a branch of mathematics concerning the study of structure, relation, and quantity. Elementary algebra is the branch that deals with solving for the operands of arithmetic equations. Modern or abstract algebra has its origins as an abstraction of elementary algebra...
, if any, is not known and it is possible that both Greek and Indian syncopation may be derived from a common Babylonian source.
Bhāskara II
Bhāskara II (1114–ca. 1185) was the leading mathematician of the 12th century. In Algebra, he gave the general solution of the Pell equation. He is the author of LilavatiLilavati
Lilavati was Indian mathematician Bhāskara II's treatise on mathematics. It is the first volume of his main work Siddhānta Shiromani, Sanskrit for "Crown of treatises," alongside Bijaganita, Grahaganita and Golādhyāya.- Name :The name comes from his daughter Līlāvatī...
and Vija-Ganita, which contain problems dealing with determinate and indeterminate linear and quadratic equations, and Pythagorean triples and he fails to distinguish between exact and approximate statements. Many of the problems in Lilavati and Vija-Ganita are derived from other Hindu sources, and so Bhaskara is at his best in dealing with indeterminate analysis.
Bhaskara uses the initial symbols of the names for colors as the symbols of unknown variables. So, for example, what we would write today as
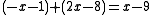
Bhaskara would have written as
-
- . _ .
- ya 1 ru 1
-
- .
-
- ya 2 ru 8
-
-
- .
-
-
- Sum ya 1 ru 9
where ya indicates the first syllable of the word for black, and ru is taken from the word species. The dots over the numbers indicate subtraction.
Islamic algebra
The first century of the IslamIslam
Islam . The most common are and . : Arabic pronunciation varies regionally. The first vowel ranges from ~~. The second vowel ranges from ~~~...
ic Arab Empire
Caliphate
The term caliphate, "dominion of a caliph " , refers to the first system of government established in Islam and represented the political unity of the Muslim Ummah...
saw almost no scientific or mathematical achievements since the Arabs, with their newly conquered empire, had not yet gained any intellectual drive and research in other parts of the world had faded. In the second half of the 8th century, Islam had a cultural awakening, and research in mathematics and the sciences increased. The Muslim Abbasid
Abbasid
The Abbasid Caliphate or, more simply, the Abbasids , was the third of the Islamic caliphates. It was ruled by the Abbasid dynasty of caliphs, who built their capital in Baghdad after overthrowing the Umayyad caliphate from all but the al-Andalus region....
caliph
Caliph
The Caliph is the head of state in a Caliphate, and the title for the ruler of the Islamic Ummah, an Islamic community ruled by the Shari'ah. It is a transcribed version of the Arabic word which means "successor" or "representative"...
al-Mamun (809–833) is said to have had a dream where Aristotle appeared to him, and as a consequence al-Mamun ordered that Arabic translation be made of as many Greek works as possible, including Ptolemy's Almagest and Euclid's Elements. Greek works would be given to the Muslims by the Byzantine Empire
Byzantine Empire
The Byzantine Empire was the Eastern Roman Empire during the periods of Late Antiquity and the Middle Ages, centred on the capital of Constantinople. Known simply as the Roman Empire or Romania to its inhabitants and neighbours, the Empire was the direct continuation of the Ancient Roman State...
in exchange for treaties, as the two empires held an uneasy peace. Many of these Greek works were translated by Thabit ibn Qurra
Thabit ibn Qurra
' was a mathematician, physician, astronomer and translator of the Islamic Golden Age.Ibn Qurra made important discoveries in algebra, geometry and astronomy...
(826–901), who translated books written by Euclid, Archimedes, Apollonius, Ptolemy, and Eutocius.
There are three theories about the origins of Arabic Algebra. The first emphasizes Hindu influence, the second emphasizes Mesopotamian or Persian-Syriac influence and the third emphasizes Greek influence. Many scholars believe that it is the result of a combination of all three sources.
Throughout their time in power, before the fall of Islamic civilization, the Arabs used a fully rhetorical algebra, where often even the numbers were spelled out in words. The Arabs would eventually replace spelled out numbers (e.g. twenty-two) with Arabic numerals
Arabic numerals
Arabic numerals or Hindu numerals or Hindu-Arabic numerals or Indo-Arabic numerals are the ten digits . They are descended from the Hindu-Arabic numeral system developed by Indian mathematicians, in which a sequence of digits such as "975" is read as a numeral...
(e.g. 22), but the Arabs never adopted or developed a syncopated or symbolic algebra, until the work of Ibn al-Banna
Ibn al-Banna
Ibn al‐Bannāʾ al‐Marrākushī al-Azdi also known as Abu'l-Abbas Ahmad ibn Muhammad ibn Uthman al-Azdi. [29) December 1256 – c. 1321) was a Moroccan mathematician, astronomer, Islamic scholar, Sufi, and a one time astrologer....
in the 13th century and Abū al-Hasan ibn Alī al-Qalasādī
Abu al-Hasan ibn Ali al-Qalasadi
Abū al-Ḥasan ibn ʿAlī ibn Muḥammad ibn ʿAlī al-Qalaṣādī was a Muslim mathematician from Al-Andalus specializing in Islamic inheritance jurisprudence...
in the 15th century.
Al-jabr wa'l muqabalah
The Muslim Persian mathematician was a faculty member of the "House of WisdomHouse of Wisdom
The House of Wisdom was a library and translation institute established in Abbassid-era Baghdad, Iraq. It was a key institution in the Translation Movement and considered to have been a major intellectual centre during the Islamic Golden Age...
" (Bait al-Hikma) in Baghdad, which was established by Al-Mamun. Al-Khwarizmi, who died around 850 CE, wrote more than half a dozen mathematical and astronomical works; some of which were based on the Indian Sindhind. One of al-Khwarizmi's most famous books is entitled Al-jabr wa'l muqabalah or The Compendious Book on Calculation by Completion and Balancing
The Compendious Book on Calculation by Completion and Balancing
, also known under a shorter name spelled as Hisab al-jabr w’al-muqabala, Kitab al-Jabr wa-l-Muqabala and other transliterations) is a mathematical book written in Arabic in approximately AD 820 by the Persian (Arabic for "The Compendious Book on Calculation by Completion and Balancing", in...
, and it gives an exhaustive account of solving polynomials up to the second degree. The book also introduced the fundamental concept of "reduction
Reduction (mathematics)
In mathematics, reduction refers to the rewriting of an expression into a simpler form. For example, the process of rewriting a fraction into one with the smallest whole-number denominator possible is called "reducing a fraction"...
" and "balancing", referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation. This is the operation which Al-Khwarizmi originally described as al-jabr.
R. Rashed and Angela Armstrong write:
Al-Jabr is divided into six chapters, each of which deals with a different type of formula. The first chapter of Al-Jabr deals with equations whose squares equal its roots (ax2 = bx), the second chapter deals with squares equal to number (ax2 = c), the third chapter deals with roots equal to a number (bx = c), the fourth chapter deals with squares and roots equal a number (ax2 + bx = c), the fifth chapter deals with squares and number equal roots (ax2 + c = bx), and the sixth and final chapter deals with roots and number equal to squares (bx + c = ax2).
In Al-Jabr, al-Khwarizmi uses geometric proofs, he does not recognize the root x = 0, and he only deals with positive roots. He also recognizes that the discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
must be positive and described the method of completing the square
Completing the square
In elementary algebra, completing the square is a technique for converting a quadratic polynomial of the formax^2 + bx + c\,\!to the formIn this context, "constant" means not depending on x. The expression inside the parenthesis is of the form ...
, though he does not justify the procedure. The Greek influence is shown by Al-Jabrs geometric foundations and by one problem taken from Heron. He makes use of lettered diagrams but all of the coefficients in all of his equations are specific numbers since he had no way of expressing with parameters what he could express geometrically; although generality of method is intended.
Al-Khwarizmi most likely did not know of Diophantus's Arithmetica, which became known to the Arabs sometime before the 10th century. And even though al-Khwarizmi most likely knew of Brahmagupta's work, Al-Jabr is fully rhetorical with the numbers even being spelled out in words. So, for example, what we would write as
Diophantus would have written as
- ΔΥα̅ ςι̅ 'ίσ Μ λ̅θ̅
And al-Khwarizmi would have written as
- One square and ten roots of the same amount to thirty-nine dirhems; that is to say, what must be the square which, when increased by ten of its own roots, amounts to thirty-nine?
Logical Necessities in Mixed Equations
'Abd al-Hamīd ibn Turk'Abd al-Hamid ibn Turk
' , known also as ' was a ninth century Turkic Muslim mathematician. Not much is known about his biography. The two records of him, one by Ibn Nadim and the other by al-Qifti are not identical. However al-Qifi mentions his name as ʿAbd al-Hamīd ibn Wase ibn Turk Jili...
authored a manuscript entitled Logical Necessities in Mixed Equations, which is very similar to al-Khwarzimi's Al-Jabr and was published at around the same time as, or even possibly earlier than, Al-Jabr. The manuscript gives exactly the same geometric demonstration as is found in Al-Jabr, and in one case the same example as found in Al-Jabr, and even goes beyond Al-Jabr by giving a geometric proof that if the discriminant is negative then the quadratic equation has no solution. The similarity between these two works has led some historians to conclude that Arabic algebra may have been well developed by the time of al-Khwarizmi and 'Abd al-Hamid.
Abu Kamil and al-Karkhi
Arabic mathematicians treated irrational numberIrrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s as algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic objects. The Egypt
Egypt
Egypt , officially the Arab Republic of Egypt, Arabic: , is a country mainly in North Africa, with the Sinai Peninsula forming a land bridge in Southwest Asia. Egypt is thus a transcontinental country, and a major power in Africa, the Mediterranean Basin, the Middle East and the Muslim world...
ian mathematician Abū Kāmil Shujā ibn Aslam (c. 850–930) was the first to accept irrational numbers (often in the form of a square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
, cube root or fourth root
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
) as solutions to quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
s or as coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s in an equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
. He was also the first to solve three non-linear simultaneous equations
Simultaneous equations
In mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations...
with three unknown variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
.
Al-Karkhi
Al-Karaji
' was a 10th century Persian Muslim mathematician and engineer. His three major works are Al-Badi' fi'l-hisab , Al-Fakhri fi'l-jabr wa'l-muqabala , and Al-Kafi fi'l-hisab .Because al-Karaji's original works in Arabic are lost, it is not...
(953–1029), also known as Al-Karaji, was the successor of Abū al-Wafā' al-Būzjānī (940–998) and he discovered the first numerical solution to equations of the form ax2n + bxn = c. Al-Karkhi only considered positive roots. Al-Karkhi is also regarded as the first person to free algebra from geometrical
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
operations and replace them with the type of arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
operations which are at the core of algebra today. His work on algebra and polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s, gave the rules for arithmetic operations to manipulate polynomials. The historian of mathematics
History of mathematics
The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past....
F. Woepcke, in Extrait du Fakhri, traité d'Algèbre par Abou Bekr Mohammed Ben Alhacan Alkarkhi (Paris
Paris
Paris is the capital and largest city in France, situated on the river Seine, in northern France, at the heart of the Île-de-France region...
, 1853), praised Al-Karaji for being "the first who introduced the theory of algebraic calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
". Stemming from this, Al-Karaji investigated binomial coefficients and Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
.
Omar Khayyám, Sharaf al-Dīn, and al-Kashi
Omar KhayyámOmar Khayyám
Omar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....
(ca. 1050–1123) wrote a book on Algebra that went beyond Al-Jabr to include equations of the third degree. Omar Khayyám provided both arithmetic and geometric solutions for quadratic equations, but he only gave geometric solutions for general cubic equations
Cubic function
In mathematics, a cubic function is a function of the formf=ax^3+bx^2+cx+d,\,where a is nonzero; or in other words, a polynomial of degree three. The derivative of a cubic function is a quadratic function...
since he mistakenly believed that arithmetic solutions were impossible. His method of solving cubic equations by using intersecting conics had been used by Menaechmus
Menaechmus
Menaechmus was an ancient Greek mathematician and geometer born in Alopeconnesus in the Thracian Chersonese, who was known for his friendship with the renowned philosopher Plato and for his apparent discovery of conic sections and his solution to the then-long-standing problem of doubling the cube...
, Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
, and Ibn al-Haytham (Alhazen), but Omar Khayyám generalized the method to cover all cubic equations with positive roots. He only considered positive roots and he did not go past the third degree. He also saw a strong relationship between Geometry and Algebra.
In the 12th century, Sharaf al-Dīn al-Tūsī (1135–1213) wrote the Al-Mu'adalat (Treatise on Equations), which dealt with eight types of cubic equations with positive solutions and five types of cubic equations which may not have positive solutions. He used what would later be known as the "Ruffini
Ruffini's rule
In mathematics, Ruffini's rule allows the rapid division of any polynomial by a binomial of the form x − r. It was described by Paolo Ruffini in 1809. Ruffini's rule is a special case of synthetic division when the divisor is a linear factor. The Horner scheme is a fast algorithm for dividing...
-Horner
Horner scheme
In numerical analysis, the Horner scheme , named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation...
method" to numerically
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
approximate the root of a cubic equation. He also developed the concepts of the maxima and minima
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
of curves in order to solve cubic equations which may not have positive solutions. He understood the importance of the discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
of the cubic equation and used an early version of Cardano
Gerolamo Cardano
Gerolamo Cardano was an Italian Renaissance mathematician, physician, astrologer and gambler...
's formula to find algebraic solutions to certain types of cubic equations. Some scholars, such as Roshdi Rashed, argue that Sharaf al-Din discovered the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of cubic polynomials and realized its significance, while other scholars connect his solution to the ideas of Euclid and Archimedes.
Sharaf al-Din also developed the concept of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. In his analysis of
the equation
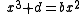for example, he begins by changing the equation's form to 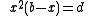. He then states that the question of whether the equation has a solution depends on whether or not the “function” on the left side reaches the value 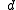. To determine this, he finds a maximum value for the function. He proves that the maximum value occurs when 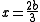, which gives the functional value 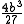. Sharaf al-Din then states that if this value is less than 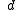, there are no positive solutions; if it is equal to 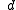, then there is one solution at 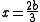; and if it is greater than 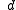, then there are two solutions, one between and and 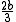one between and 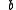.In the early 15th century, Jamshīd al-Kāshī
Jamshid al-Kashi
Ghiyāth al-Dīn Jamshīd Masʾūd al-Kāshī was a Persian astronomer and mathematician.-Biography:...
developed an early form of Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
to numerically solve the equation
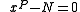to find roots of 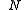. Al-Kāshī also developed decimal fractions and claimed to have discovered it himself. However, J. Lennart Berggrenn notes that he was mistaken, as decimal fractions were first used five centuries before him by the BaghdadBaghdad
Baghdad is the capital of Iraq, as well as the coterminous Baghdad Governorate. The population of Baghdad in 2011 is approximately 7,216,040...
i mathematician Abu'l-Hasan al-Uqlidisi
Abu'l-Hasan al-Uqlidisi
Abu'l Hasan Ahmad ibn Ibrahim Al-Uqlidisi was an Arab mathematician who was active in Damascus and Baghdad. As his surname indicates, he was a copyist of Euclid's works. He wrote the earliest surviving book on the positional use of the Arabic numerals, Kitab al-Fusul fi al-Hisab al-Hindi around 952...
as early as the 10th century.
Al-Hassār, Ibn al-Banna, and al-Qalasadi
Al-Hassār, a mathematician from MoroccoMorocco
Morocco , officially the Kingdom of Morocco , is a country located in North Africa. It has a population of more than 32 million and an area of 710,850 km², and also primarily administers the disputed region of the Western Sahara...
specializing in Islamic inheritance jurisprudence
Islamic inheritance jurisprudence
Islamic Inheritance jurisprudence is a field of Islamic Jurisprudence that deals with inheritance, a topic that is prominently dealt with in the Qur'an. It is often called Mīrāth, and its branch of Islamic law is technically known as ʿulm al-farāʾiḍ...
during the 12th century, developed the modern symbolic mathematical notation
Mathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
for fractions
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
, where the numerator and denominator are separated by a horizontal bar. This same fractional notation appeared soon after in the work of Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
in the 13th century.
Abū al-Hasan ibn Alī al-Qalasādī
Abu al-Hasan ibn Ali al-Qalasadi
Abū al-Ḥasan ibn ʿAlī ibn Muḥammad ibn ʿAlī al-Qalaṣādī was a Muslim mathematician from Al-Andalus specializing in Islamic inheritance jurisprudence...
(1412–1482) was the last major medieval Arab
Arab
Arab people, also known as Arabs , are a panethnicity primarily living in the Arab world, which is located in Western Asia and North Africa. They are identified as such on one or more of genealogical, linguistic, or cultural grounds, with tribal affiliations, and intra-tribal relationships playing...
algebraist, who made the first attempt at creating an algebraic notation
Mathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
since Ibn al-Banna
Ibn al-Banna
Ibn al‐Bannāʾ al‐Marrākushī al-Azdi also known as Abu'l-Abbas Ahmad ibn Muhammad ibn Uthman al-Azdi. [29) December 1256 – c. 1321) was a Moroccan mathematician, astronomer, Islamic scholar, Sufi, and a one time astrologer....
two centuries earlier, who was himself the first to make such an attempt since Diophantus
Diophantus
Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
and Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
in ancient times. The syncopated notations of his predecessors, however, lacked symbols for mathematical operations
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
. Al-Qalasadi "took the first steps toward the introduction of algebraic symbolism by using letters in place of numbers" and by "using short Arabic words, or just their initial letters, as mathematical symbols."
Dark Ages
Just as the death of Hypatia signals the close of the Library of AlexandriaLibrary of Alexandria
The Royal Library of Alexandria, or Ancient Library of Alexandria, in Alexandria, Egypt, was the largest and most significant great library of the ancient world. It flourished under the patronage of the Ptolemaic dynasty and functioned as a major center of scholarship from its construction in the...
as a mathematical center, so does the death of Boethius signal the end of mathematics in the Western Roman Empire
Western Roman Empire
The Western Roman Empire was the western half of the Roman Empire after its division by Diocletian in 285; the other half of the Roman Empire was the Eastern Roman Empire, commonly referred to today as the Byzantine Empire....
. Although there was some work being done at Athens
Athens
Athens , is the capital and largest city of Greece. Athens dominates the Attica region and is one of the world's oldest cities, as its recorded history spans around 3,400 years. Classical Athens was a powerful city-state...
, it came to a close when in 529
529
Year 529 was a common year starting on Monday of the Julian calendar. At the time, it was known as the Year of the Consulship of Decius without colleague...
the Byzantine
Byzantine
Byzantine usually refers to the Roman Empire during the Middle Ages.Byzantine may also refer to:* A citizen of the Byzantine Empire, or native Greek during the Middle Ages...
emperor Justinian closed the pagan philosophical schools. The year 529
529
Year 529 was a common year starting on Monday of the Julian calendar. At the time, it was known as the Year of the Consulship of Decius without colleague...
is now taken to be the beginning of the medieval period. Scholars fled the West towards the more hospitable East, particularly towards Persia, where they found haven under King Chosroes
Khosrau I
Khosrau I , also known as Anushiravan the Just or Anushirawan the Just Khosrau I (also called Chosroes I in classical sources, most commonly known in Persian as Anushirvan or Anushirwan, Persian: انوشيروان meaning the immortal soul), also known as Anushiravan the Just or Anushirawan the Just...
and established what might be termed an "Athenian Academy in Exile". Under a treaty with Justinian, Chosroes would eventually return the scholars to the Eastern Empire. During the Dark Ages, European mathematics was at its nadir with mathematical research consisting mainly of commentaries on ancient treatises; and most of this research was centered in the Byzantine Empire
Byzantine Empire
The Byzantine Empire was the Eastern Roman Empire during the periods of Late Antiquity and the Middle Ages, centred on the capital of Constantinople. Known simply as the Roman Empire or Romania to its inhabitants and neighbours, the Empire was the direct continuation of the Ancient Roman State...
. The end of the medieval period is set as the fall of Constantinople
Constantinople
Constantinople was the capital of the Roman, Eastern Roman, Byzantine, Latin, and Ottoman Empires. Throughout most of the Middle Ages, Constantinople was Europe's largest and wealthiest city.-Names:...
to the Turks
Ottoman Empire
The Ottoman EmpireIt was usually referred to as the "Ottoman Empire", the "Turkish Empire", the "Ottoman Caliphate" or more commonly "Turkey" by its contemporaries...
in 1453.
Late Middle Ages
The 12th century saw a flood of translations from Arabic into LatinLatin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
and by the 13th century, European mathematics was beginning to rival the mathematics of other lands. In the 13th century, the solution of a cubic equation by Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
is representative of the beginning of a revival in European algebra.
As the Islamic world was declining after the 15th century, the European world was ascending. And it is here that Algebra was further developed.
Modern algebra
Another key event in the further development of algebra was the general algebraic solution of the cubic and quartic equations, developed in the mid-16th century. The idea of a determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
was developed by Japanese mathematician
Japanese mathematics
denotes a distinct kind of mathematics which was developed in Japan during the Edo Period . The term wasan, from wa and san , was coined in the 1870s and employed to distinguish native Japanese mathematics theory from Western mathematics .In the history of mathematics, the development of wasan...
Kowa Seki in the 17th century, followed by Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
ten years later, for the purpose of solving systems of simultaneous linear equations using matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. Gabriel Cramer
Gabriel Cramer
Gabriel Cramer was a Swiss mathematician, born in Geneva. He showed promise in mathematics from an early age. At 18 he received his doctorate and at 20 he was co-chair of mathematics.In 1728 he proposed a solution to the St...
also did some work on matrices and determinants in the 18th century.
The symbol
Symbol
A symbol is something which represents an idea, a physical entity or a process but is distinct from it. The purpose of a symbol is to communicate meaning. For example, a red octagon may be a symbol for "STOP". On a map, a picture of a tent might represent a campsite. Numerals are symbols for...
commonly denotes an unknown variableVariable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
. Even though any letter can be used,
is the most common choice. This usage can be traced back to the ArabicArabic language
Arabic is a name applied to the descendants of the Classical Arabic language of the 6th century AD, used most prominently in the Quran, the Islamic Holy Book...
word šay
The Compendious Book on Calculation by Completion and Balancing
, also known under a shorter name spelled as Hisab al-jabr w’al-muqabala, Kitab al-Jabr wa-l-Muqabala and other transliterations) is a mathematical book written in Arabic in approximately AD 820 by the Persian (Arabic for "The Compendious Book on Calculation by Completion and Balancing", in...
, and was taken into Old Spanish
Old Spanish language
Old Spanish, also known as Old Castilian or Mediaeval Spanish , is an early form of the Spanish language that was spoken on the Iberian Peninsula from the tenth century until roughly the beginning of the fifteenth century, before a consonantic readjustment gave rise to the evolution of modern...
with the pronunciation “šei,” which was written xei, and was soon habitually abbreviated to
. (The SpanishSpanish language
Spanish , also known as Castilian , is a Romance language in the Ibero-Romance group that evolved from several languages and dialects in central-northern Iberia around the 9th century and gradually spread with the expansion of the Kingdom of Castile into central and southern Iberia during the...
pronunciation
Pronunciation
Pronunciation refers to the way a word or a language is spoken, or the manner in which someone utters a word. If one is said to have "correct pronunciation", then it refers to both within a particular dialect....
of “x” has changed since). Some sources say that this
is an abbreviation of LatinLatin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
causa, which was a translation of Arabic شيء. This started the habit of using letters to represent quantities in algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
. In mathematics, an “italicized
Italic type
In typography, italic type is a cursive typeface based on a stylized form of calligraphic handwriting. Owing to the influence from calligraphy, such typefaces often slant slightly to the right. Different glyph shapes from roman type are also usually used—another influence from calligraphy...
x” (
) is often used to avoid potential confusion with the multiplication symbol.Gottfried Leibniz
Although the mathematical notion of functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
was implicit in trigonometric and logarithmic tables, which existed in his day, Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
was the first, in 1692 and 1694, to employ it explicitly, to denote any of several geometric concepts derived from a curve, such as abscissa
Abscissa
In mathematics, abscissa refers to that element of an ordered pair which is plotted on the horizontal axis of a two-dimensional Cartesian coordinate system, as opposed to the ordinate...
, ordinate
Ordinate
In mathematics, ordinate refers to that element of an ordered pair which is plotted on the vertical axis of a two-dimensional Cartesian coordinate system, as opposed to the abscissa...
, tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
, chord
Chord (geometry)
A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
, and the perpendicular. In the 18th century, "function" lost these geometrical associations.
Leibniz realized that the coefficients of a system of linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
s could be arranged into an array, now called a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, which can be manipulated to find the solution of the system, if any. This method was later called Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
. Leibniz also discovered Boolean algebra and symbolic logic, also relevant to algebra.
Abstract algebra
Abstract algebraAbstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
was developed in the 19th century, initially focusing on what is now called Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, and on constructibility
Constructible number
A point in the Euclidean plane is a constructible point if, given a fixed coordinate system , the point can be constructed with unruled straightedge and compass...
issues.
The father of algebra
The HellenisticHellenistic civilization
Hellenistic civilization represents the zenith of Greek influence in the ancient world from 323 BCE to about 146 BCE...
mathematician Diophantus
Diophantus
Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
has traditionally been known as "the father of algebra" but debate now exists as to whether or not Al-Khwarizmi
Muhammad ibn Musa al-Khwarizmi
'There is some confusion in the literature on whether al-Khwārizmī's full name is ' or '. Ibn Khaldun notes in his encyclopedic work: "The first who wrote upon this branch was Abu ʿAbdallah al-Khowarizmi, after whom came Abu Kamil Shojaʿ ibn Aslam." . 'There is some confusion in the literature on...
deserves this title instead. Those who support Diophantus point to the fact that the algebra found in Al-Jabr
The Compendious Book on Calculation by Completion and Balancing
, also known under a shorter name spelled as Hisab al-jabr w’al-muqabala, Kitab al-Jabr wa-l-Muqabala and other transliterations) is a mathematical book written in Arabic in approximately AD 820 by the Persian (Arabic for "The Compendious Book on Calculation by Completion and Balancing", in...
is more elementary than the algebra found in Arithmetica
Arithmetica
Arithmetica is an ancient Greek text on mathematics written by the mathematician Diophantus in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate equations and indeterminate equations.Equations in the book are called Diophantine equations...
and that Arithmetica is syncopated while Al-Jabr is fully rhetorical.
Those who support Al-Khwarizmi point to the fact that he gave an exhaustive explanation for the algebraic solution of quadratic equations with positive roots, and was the first to teach algebra in an elementary form
Elementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
and for its own sake, whereas Diophantus was primarily concerned with the theory of numbers
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. Al-Khwarizmi also introduced the fundamental concept of "reduction" and "balancing" (which he originally used the term al-jabr to refer to), referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation. Other supporters of Al-Khwarizmi point to his algebra no longer being concerned "with a series of problem
Problem
A problem is an obstacle, impediment, difficulty or challenge, or any situation that invites resolution; the resolution of which is recognized as a solution or contribution toward a known purpose or goal...
s to be resolved, but an exposition
Expository writing
Expository writing is a type of writing where the purpose is to inform, explain, describe, or define the author's subject to the reader. Expository text is meant to deposit information and is the most frequently used type of writing by students in colleges and universities. A well-written...
which starts with primitive terms in which the combinations must give all possible prototypes for equations, which henceforward explicitly constitute the true object of study." They also point to his treatment of an equation for its own sake and "in a generic manner, insofar as it does not simply emerge in the course of solving a problem, but is specifically called on to define an infinite class of problems." Al-Khwarizmi's work established algebra as a mathematical discipline that is independent of geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
.