Hill climbing
Encyclopedia
In computer science
, hill climbing is a mathematical optimization
technique which belongs to the family of local search
. It is an iterative algorithm that starts with an arbitrary solution to a problem, then attempts to find a better solution by incrementally
changing a single element of the solution. If the change produces a better solution, an incremental change is made to the new solution, repeating until no further improvements can be found.
For example, hill climbing can be applied to the travelling salesman problem
. It is easy to find an initial solution that visits all the cities but will be very poor compared to the optimal solution. The algorithm starts with such a solution and makes small improvements to it, such as switching the order in which two cities are visited. Eventually, a much shorter route is likely to be obtained.
Hill climbing is good for finding a local optimum
(a solution that cannot be improved by considering a neighboring configuration) but it is not guaranteed to find the best possible solution (the global optimum
) out of all possible solutions (the search space
).
The characteristic that only local optima are guaranteed can be cured by using restarts (repeated local search), or more complex schemes based
on iterations, like iterated local search
, on memory,
like reactive search optimization
and tabu search
,
on memory-less stochastic modifications, like simulated annealing
.
The relative simplicity of the algorithm makes it a popular first choice amongst optimizing algorithms. It is used widely in artificial intelligence
, for reaching a goal state from a starting node. Choice of next node and starting node can be varied to give a list of related algorithms. Although more advanced algorithms such as simulated annealing
or tabu search
may give better results, in some situations hill climbing works just as well. Hill climbing can often produce a better result than other algorithms when the amount of time available to perform a search is limited, such as with real-time systems.
It is an anytime algorithm
:
it can return a valid solution even if it's interrupted at any time before it ends.
, where 
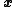is a vector of continuous and/or discrete values. At each iteration, hill climbing will adjust a single element in 
and determine whether the change improves the value of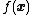 
. (Note that this differs from gradient descent
methods, which adjust all of the values in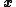
at each iteration according to the gradient of the hill.) With hill climbing, any change that improves 
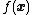is accepted, and the process continues until no change can be found to improve the value of 
. 
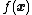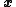is then said to be "locally optimal".
In discrete vector spaces, each possible value for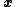
may be visualized as a vertex
in a graph
. Hill climbing will follow the graph from vertex to vertex, always locally increasing (or decreasing) the value of
, until a local maximum (or local minimum)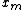 
is reached.
, which tries all possible extensions of the current path instead of only one.
Stochastic hill climbing
does not examine all neighbors before deciding how to move. Rather, it selects a neighbor at random, and decides (based on the amount of improvement in that neighbor) whether to move to that neighbor or to examine another.
Random-restart hill climbing is a meta-algorithm built on top of the hill climbing algorithm. It is also known as Shotgun hill climbing. It iteratively does hill-climbing, each time with a random initial condition
. The best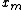 
is kept: if a new run of hill climbing produces a better 
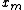than the stored state, it replaces the stored state.
Random-restart hill climbing is a surprisingly effective algorithm in many cases. It turns out that it is often better to spend CPU time exploring the space, than carefully optimizing from an initial condition.
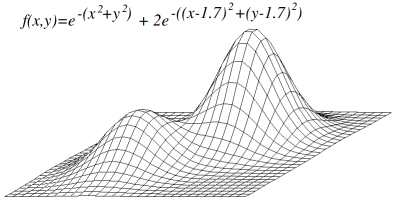A problem with hill climbing is that it will find only local maxima
. Unless the heuristic is convex, it may not reach a global maximum. Other local search algorithms try to overcome this problem such as stochastic hill climbing
, random walk
s and simulated annealing
.
By contrast, gradient descent methods can move in any direction that the ridge or alley may ascend or descend. Hence, gradient descent is generally preferred over hill climbing when the target function is differentiable. Hill climbers, however, have the advantage of not requiring the target function to be differentiable, so hill climbers may be preferred when the target function is complex.
Contrast genetic algorithm
; random optimization
.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, hill climbing is a mathematical optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
technique which belongs to the family of local search
Local search (optimization)
In computer science, local search is a metaheuristic method for solving computationally hard optimization problems. Local search can be used on problems that can be formulated as finding a solution maximizing a criterion among a number of candidate solutions...
. It is an iterative algorithm that starts with an arbitrary solution to a problem, then attempts to find a better solution by incrementally
Incremental heuristic search
Incremental heuristic search algorithms combine both incremental and heuristic search to speed up searches of sequences of similar search problems, which is important in domains that are only incompletely known or change dynamically. Incremental search has been studied at least since the late 1960s...
changing a single element of the solution. If the change produces a better solution, an incremental change is made to the new solution, repeating until no further improvements can be found.
For example, hill climbing can be applied to the travelling salesman problem
Travelling salesman problem
The travelling salesman problem is an NP-hard problem in combinatorial optimization studied in operations research and theoretical computer science. Given a list of cities and their pairwise distances, the task is to find the shortest possible tour that visits each city exactly once...
. It is easy to find an initial solution that visits all the cities but will be very poor compared to the optimal solution. The algorithm starts with such a solution and makes small improvements to it, such as switching the order in which two cities are visited. Eventually, a much shorter route is likely to be obtained.
Hill climbing is good for finding a local optimum
Local optimum
Local optimum is a term in applied mathematics and computer science.A local optimum of a combinatorial optimization problem is a solution that is optimal within a neighboring set of solutions...
(a solution that cannot be improved by considering a neighboring configuration) but it is not guaranteed to find the best possible solution (the global optimum
Global optimum
In mathematics, a global optimum is a selection from a given domain which yields either the highest value or lowest value , when a specific function is applied. For example, for the function...
) out of all possible solutions (the search space
Search space
Search space may refer to one of the following.*In optimization, the domain of the function to be optimized*In search algorithms of computer science, the set of all possible solutions...
).
The characteristic that only local optima are guaranteed can be cured by using restarts (repeated local search), or more complex schemes based
on iterations, like iterated local search
Iterated local search
Iterated local search is a term in applied mathematics and computer sciencedefining a modification of local search or hill climbing methods for solving discrete optimization problems.Local search methods build a trajectory in configuration...
, on memory,
like reactive search optimization
Reactive search optimization
Reactive search optimization defines local-search heuristics based on machine learning, a family of optimization algorithms based on the local search techniques...
and tabu search
Tabu search
Tabu search is a mathematical optimization method, belonging to the class of trajectory based techniques. Tabu search enhances the performance of a local search method by using memory structures that describe the visited solutions: once a potential solution has been determined, it is marked as...
,
on memory-less stochastic modifications, like simulated annealing
Simulated annealing
Simulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...
.
The relative simplicity of the algorithm makes it a popular first choice amongst optimizing algorithms. It is used widely in artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
, for reaching a goal state from a starting node. Choice of next node and starting node can be varied to give a list of related algorithms. Although more advanced algorithms such as simulated annealing
Simulated annealing
Simulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...
or tabu search
Tabu search
Tabu search is a mathematical optimization method, belonging to the class of trajectory based techniques. Tabu search enhances the performance of a local search method by using memory structures that describe the visited solutions: once a potential solution has been determined, it is marked as...
may give better results, in some situations hill climbing works just as well. Hill climbing can often produce a better result than other algorithms when the amount of time available to perform a search is limited, such as with real-time systems.
It is an anytime algorithm
Anytime algorithm
In computer science an anytime algorithm is an algorithm that can return a valid solution to a problem even if it's interrupted at any time before it ends. The algorithm is expected to find better and better solutions the more time it keeps running....
:
it can return a valid solution even if it's interrupted at any time before it ends.
Mathematical description
Hill climbing attempts to maximize (or minimize) a target functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
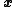, where is a vector of continuous and/or discrete values. At each iteration, hill climbing will adjust a single element in and determine whether the change improves the value of 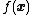. (Note that this differs from gradient descentGradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
methods, which adjust all of the values in
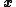at each iteration according to the gradient of the hill.) With hill climbing, any change that improves 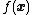is accepted, and the process continues until no change can be found to improve the value of 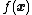. 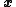is then said to be "locally optimal".In discrete vector spaces, each possible value for
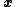may be visualized as a vertexVertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
in a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
. Hill climbing will follow the graph from vertex to vertex, always locally increasing (or decreasing) the value of
, until a local maximum (or local minimum) 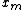is reached.Variants
In simple hill climbing, the first closer node is chosen, whereas in steepest ascent hill climbing all successors are compared and the closest to the solution is chosen. Both forms fail if there is no closer node, which may happen if there are local maxima in the search space which are not solutions. Steepest ascent hill climbing is similar to best-first searchBest-first search
Best-first search is a search algorithm which explores a graph by expanding the most promising node chosen according to a specified rule.Judea Pearl described best-first search as estimating the promise of node n by a "heuristic evaluation function f which, in general, may depend on the description...
, which tries all possible extensions of the current path instead of only one.
Stochastic hill climbing
Stochastic hill climbing
Stochastic hill climbing is a variant of the basic hill climbing method. While basic hill climbing always chooses the steepest uphill move, stochastic hill climbing chooses at random from among the uphill moves. The probability of selection may vary with the steepness of the uphill move....
does not examine all neighbors before deciding how to move. Rather, it selects a neighbor at random, and decides (based on the amount of improvement in that neighbor) whether to move to that neighbor or to examine another.
Random-restart hill climbing is a meta-algorithm built on top of the hill climbing algorithm. It is also known as Shotgun hill climbing. It iteratively does hill-climbing, each time with a random initial condition
. The best 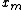is kept: if a new run of hill climbing produces a better 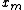than the stored state, it replaces the stored state.Random-restart hill climbing is a surprisingly effective algorithm in many cases. It turns out that it is often better to spend CPU time exploring the space, than carefully optimizing from an initial condition.
Local maxima
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
. Unless the heuristic is convex, it may not reach a global maximum. Other local search algorithms try to overcome this problem such as stochastic hill climbing
Stochastic hill climbing
Stochastic hill climbing is a variant of the basic hill climbing method. While basic hill climbing always chooses the steepest uphill move, stochastic hill climbing chooses at random from among the uphill moves. The probability of selection may vary with the steepness of the uphill move....
, random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
s and simulated annealing
Simulated annealing
Simulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...
.
Ridges and Alleys
Ridges are a challenging problem for hill climbers that optimize in continuous spaces. Because hill climbers only adjust one element in the vector at a time, each step will move in an axis-aligned direction. If the target function creates a narrow ridge that ascends in a non-axis-aligned direction (or if the goal is to minimize, a narrow alley that descends in a non-axis-aligned direction), then the hill climber can only ascend the ridge (or descend the alley) by zig-zagging. If the sides of the ridge (or alley) are very steep, then the hill climber may be forced to take very tiny steps as it zig-zags toward a better position. Thus, it may take an unreasonable length of time for it to ascend the ridge (or descend the alley).By contrast, gradient descent methods can move in any direction that the ridge or alley may ascend or descend. Hence, gradient descent is generally preferred over hill climbing when the target function is differentiable. Hill climbers, however, have the advantage of not requiring the target function to be differentiable, so hill climbers may be preferred when the target function is complex.
Plateau
Another problem that sometimes occurs with hill climbing is that of a plateau. A plateau is encountered when the search space is flat, or sufficiently flat that the value returned by the target function is indistinguishable from the value returned for nearby regions due to the precision used by the machine to represent its value. In such cases, the hill climber may not be able to determine in which direction it should step, and may wander in a direction that never leads to improvement.Pseudocode
Discrete Space Hill Climbing Algorithm
currentNode = startNode;
loop do
L = NEIGHBORS(currentNode);
nextEval = -INF;
nextNode = NULL;
for all x in L
if (EVAL(x) > nextEval)
nextNode = x;
nextEval = EVAL(x);
if nextEval <= EVAL(currentNode)
//Return current node since no better neighbors exist
return currentNode;
currentNode = nextNode;
Continuous Space Hill Climbing Algorithm
currentPoint = initialPoint; // the zero-magnitude vector is common
stepSize = initialStepSizes; // a vector of all 1's is common
acceleration = someAcceleration; // a value such as 1.2 is common
candidate[0] = -acceleration;
candidate[1] = -1 / acceleration;
candidate[2] = 0;
candidate[3] = 1 / acceleration;
candidate[4] = acceleration;
loop do
before = EVAL(currentPoint);
for each element i in currentPoint do
best = -1;
bestScore = -INF;
for j from 0 to 4 // try each of 5 candidate locations
currentPoint[i] = currentPoint[i] + stepSize[i] * candidate[j];
temp = EVAL(currentPoint);
currentPoint[i] = currentPoint[i] - stepSize[i] * candidate[j];
if(temp > bestScore)
bestScore = temp;
best = j;
if candidate[best] is not 0
currentPoint[i] = currentPoint[i] + stepSize[i] * candidate[best];
stepSize[i] = stepSize[i] * candidate[best]; // accelerate
if (EVAL(currentPoint) - before) < epsilon
return currentPoint;
Contrast genetic algorithm
Genetic algorithm
A genetic algorithm is a search heuristic that mimics the process of natural evolution. This heuristic is routinely used to generate useful solutions to optimization and search problems...
; random optimization
Random optimization
Random optimization is a family of numerical optimization methods that do not require the gradient of the problem to be optimized and RO can hence be used on functions that are not continuous or differentiable...
.
See also
- Gradient descentGradient descentGradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
- Greedy algorithmGreedy algorithmA greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
- TâtonnementWalrasian auctionA Walrasian auction, introduced by Leon Walras, is a type of simultaneous auction where each agent calculates its demand for the good at every possible price and submits this to an auctioneer. The price is then set so that the total demand across all agents equals the total amount of the good...
- Mean-shiftMean-shiftMean shift is a non-parametric feature-space analysis technique, a so-called mode seeking algorithm. Application domains include clustering in computer vision and image processing.- Overview :...
External links
- Hill Climbing visualization A visualization of a hill-climbing (greedy) solution to the N-Queens puzzle by Yuval Baror.