Hilbert class field
Encyclopedia
In algebraic number theory
, the Hilbert class field E of a number field K is the maximal abelian unramified extension of K. Its degree over K equals the class number of K and the Galois group
of E over K is canonically isomorphic to the ideal class group
of K using Frobenius elements for prime ideal
s in K.
Note that in this context, the Hilbert class field of K is not just unramified at the finite places (the classical ideal theoretic interpretation) but also at the infinite places of K. That is, every real embedding of K extends to a real embedding of E (rather than to a complex embedding of E).
, in particular, if
then K is its own Hilbert class field.
By contrast, let
. By analyzing ramification degrees over 
, one can show that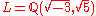 
is an everywhere unramified extension of K, and it is certainly abelian. Hence the Hilbert class field of K is a nontrivial extension and the ring of integers of K cannot be a unique factorization domain. (In fact, using the Minkowski bound, one can show that K has class number exactly 2.) Hence, the Hilbert class field is 
.
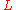To see why ramification at the archimedean primes must be taken into account, consider the real
quadratic field
K obtained by adjoining the square root of 3 to Q. This field has class number 1, but the extension K(i)/K is unramified at all prime ideals in K, so K admits finite abelian extensions of degree greater than 1
in which all primes of K are unramified. This doesn't contradict the Hilbert class field of K being K itself: every proper finite abelian extension of K
must ramify at some place, and in the extension K(i)/K there is ramification at the archimedean places:
the real embeddings of K extend to complex (rather than real) embeddings of K(i).
and proved by Philipp Furtwängler
. The existence of the Hilbert class field is a valuable tool in studying the structure of the ideal class group
of a given field.
In fact, E is the unique field
satisfying the first, second, and fourth properties.
with complex multiplication
by the ring of integers
of K, then adjoining the j-invariant
of A to K gives the Hilbert class field.
, one studies the ray class field with respect to a given modulus
, which is a formal product of prime ideals (including, possibly, archimedean ones). The ray class field is the maximal abelian extension unramified outside the primes dividing the modulus and satisfying a particular ramification condition at the primes dividing the modulus. The Hilbert class field is then the ray class field with respect to the trivial modulus 1.
The narrow class field is the Hilbert class field with respect to the modulus consisting of all infinite primes. For example, the argument above shows that
is the narrow class field of 
.
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, the Hilbert class field E of a number field K is the maximal abelian unramified extension of K. Its degree over K equals the class number of K and the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of E over K is canonically isomorphic to the ideal class group
Ideal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
of K using Frobenius elements for prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s in K.
Note that in this context, the Hilbert class field of K is not just unramified at the finite places (the classical ideal theoretic interpretation) but also at the infinite places of K. That is, every real embedding of K extends to a real embedding of E (rather than to a complex embedding of E).
Examples
If the ring of integers of K is a unique factorization domainUnique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
, in particular, if
then K is its own Hilbert class field.By contrast, let
. By analyzing ramification degrees over , one can show that 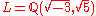is an everywhere unramified extension of K, and it is certainly abelian. Hence the Hilbert class field of K is a nontrivial extension and the ring of integers of K cannot be a unique factorization domain. (In fact, using the Minkowski bound, one can show that K has class number exactly 2.) Hence, the Hilbert class field is 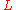.To see why ramification at the archimedean primes must be taken into account, consider the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
K obtained by adjoining the square root of 3 to Q. This field has class number 1, but the extension K(i)/K is unramified at all prime ideals in K, so K admits finite abelian extensions of degree greater than 1
in which all primes of K are unramified. This doesn't contradict the Hilbert class field of K being K itself: every proper finite abelian extension of K
must ramify at some place, and in the extension K(i)/K there is ramification at the archimedean places:
the real embeddings of K extend to complex (rather than real) embeddings of K(i).
History
The existence of a Hilbert class field for a given number field K was conjectured by David HilbertDavid Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
and proved by Philipp Furtwängler
Philipp Furtwängler
Philipp Furtwängler was a German number theorist.He wrote an 1896 doctoral dissertation at the University of Göttingen on cubic forms , under Felix Klein...
. The existence of the Hilbert class field is a valuable tool in studying the structure of the ideal class group
Ideal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
of a given field.
Additional properties
The Hilbert class field E also satisfies the following:- E is a finite Galois extensionField extensionIn abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of K and [E : K]=hK, where hK is the class number of K. - The ideal class groupIdeal class groupIn mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
of K is isomorphicAutomorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
to the Galois groupGalois groupIn mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of E over K. - Every idealIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of OK is a principal idealPrincipal idealIn ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
of the ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
extensionDegree (mathematics)In mathematics, there are several meanings of degree depending on the subject.- Unit of angle :A degree , usually denoted by ° , is a measurement of a plane angle, representing 1⁄360 of a turn...
OE (principal ideal theoremPrincipal ideal theoremIn mathematics, the principal ideal theorem of class field theory, a branch of algebraic number theory, is the statement that for any algebraic number field K and any ideal I of the ring of integers of K, if L is the Hilbert class field of K, thenIO_L\ is a principal ideal αOL, for OL the ring of...
). - Every prime idealPrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
P of OK decomposes into the product of hK/f prime ideals in OE, where f is the order of [P] in the ideal class group of OK.
In fact, E is the unique field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
satisfying the first, second, and fourth properties.
Explicit constructions
If K is imaginary quadratic and A is an elliptic curveElliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
with complex multiplication
Complex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
by the ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
of K, then adjoining the j-invariant
J-invariant
In mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function defined on the upper half-plane of complex numbers.We haveThe modular discriminant \Delta is defined as \Delta=g_2^3-27g_3^2...
of A to K gives the Hilbert class field.
Generalizations
In class field theoryClass field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
, one studies the ray class field with respect to a given modulus
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, which is a formal product of prime ideals (including, possibly, archimedean ones). The ray class field is the maximal abelian extension unramified outside the primes dividing the modulus and satisfying a particular ramification condition at the primes dividing the modulus. The Hilbert class field is then the ray class field with respect to the trivial modulus 1.
The narrow class field is the Hilbert class field with respect to the modulus consisting of all infinite primes. For example, the argument above shows that
is the narrow class field of .