
Hearing the shape of a drum
Encyclopedia

Drumhead
A drumhead is a membrane stretched over one or both of the open ends of a drum. The drumhead is struck with sticks, mallets, or hands so that it vibrates and the sound resonates through the drum.-History:...
from the sound it makes, i.e., from the list of basic harmonics
Harmonic series (music)
Pitched musical instruments are often based on an approximate harmonic oscillator such as a string or a column of air, which oscillates at numerous frequencies simultaneously. At these resonant frequencies, waves travel in both directions along the string or air column, reinforcing and canceling...
, via the use of mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
theory. "Can One Hear the Shape of a Drum?" was the witty title of an article by Mark Kac
Mark Kac
Mark Kac was a Polish mathematician. His main interest was probability theory. His question, "Can one hear the shape of a drum?" set off research into spectral theory, with the idea of understanding the extent to which the spectrum allows one to read back the geometry. Kac completed his Ph.D...
in the American Mathematical Monthly
American Mathematical Monthly
The American Mathematical Monthly is a mathematical journal founded by Benjamin Finkel in 1894. It is currently published 10 times each year by the Mathematical Association of America....
1966 (see the references below), but these questions can be traced back all the way to Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
.
The frequencies at which a drumhead can vibrate depend on its shape. The Helmholtz equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
tells us the frequencies if we know the shape. These frequencies are the eigenvalues of the Laplacian in the region. A central question is: can they tell us the shape if we know the frequencies? No other shape than a square vibrates at the same frequencies as a square. Is it possible for two different shapes to yield the same set of frequencies? Kac did not know the answer to that question.
Formal statement
More formally, the drum is conceived as an elastic membrane whose boundary is clamped. It is represented as a domainDomain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
D in the plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
. Denote by λn the Dirichlet eigenvalue
Dirichlet eigenvalue
In mathematics, the Dirichlet eigenvalues are the fundamental modes of vibration of an idealized drum with a given shape. The problem of whether one can hear the shape of a drum is: given the Dirichlet eigenvalues, what features of the shape of the drum can one deduce. Here a "drum" is thought of...
s for D: that is, the eigenvalues of the Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
for the Laplacian:

Two domains are said to be isospectral
Isospectral
In mathematics, two linear operators are called isospectral or cospectral if they have the same spectrum. Roughly speaking, they are supposed to have the same sets of eigenvalues, when those are counted with multiplicity....
(or homophonic) if they have the same eigenvalues. The term "homophonic" is justified because the Dirichlet eigenvalues are precisely the fundamental tones that the drum is capable of producing: they appear naturally as Fourier coefficients
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
in the solution wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
with clamped boundary.
Therefore the question may be reformulated as: what can be inferred on D if one knows only the values of λn? Or, more specifically: are there two distinct domains that are isospectral?
Related problems can be formulated for the Dirichlet problem for the Laplacian on domains in higher dimensions or on Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s, as well as for other elliptic differential operators such as the Cauchy–Riemann operator or Dirac operator
Dirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
. Other boundary conditions besides the Dirichlet condition, such as the Neumann boundary condition
Neumann boundary condition
In mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
, can be imposed. See spectral geometry
Spectral geometry
Spectral geometry is a field in mathematics which concerns relationships between geometric structures of manifolds and spectra of canonically defined differential operators. The case of the Laplace–Beltrami operator on a closed Riemannian manifold has been most intensively studied, although other...
and isospectral
Isospectral
In mathematics, two linear operators are called isospectral or cospectral if they have the same spectrum. Roughly speaking, they are supposed to have the same sets of eigenvalues, when those are counted with multiplicity....
as related articles.
The answer
Almost immediately, John MilnorJohn Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
observed that a theorem due to Ernst Witt
Ernst Witt
Ernst Witt was a German mathematician born on the island of Als . Shortly after his birth, he and his parents moved to China, and he did not return to Europe until he was nine....
implied the existence of a pair of 16-dimensional tori that have the same eigenvalues but different shapes. However, the problem in two dimensions remained open until 1992, when Gordon, Webb, and Wolpert constructed, based on the Sunada method
Toshikazu Sunada
is a Japanese mathematician and author of many books and essays on mathematics and mathematical sciences. He is professor of mathematics at Meiji University, Tokyo, and is also professor emeritus of Tohoku University, Tohoku, Japan...
, a pair of regions in the plane that have different shapes but identical eigenvalues. The regions are non-convex polygon
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
s (see picture). The proof that both regions have the same eigenvalues is rather elementary and uses the symmetries of the Laplacian. This idea has been generalized by Buser et al., who constructed numerous similar examples. So, the answer to Kac's question is: for many shapes, one cannot hear the shape of the drum completely. However, some information can be inferred.
On the other hand, Steve Zelditch proved that the answer to Kac's question is positive if one imposes restrictions to certain convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
planar regions with analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
boundary. It is not known whether two non-convex analytic domains can have the same eigenvalues. It is known that the set of domains isospectral with a given one is compact in the C∞ topology. Moreover, the sphere (for instance) is spectrally rigid, by Cheng's eigenvalue comparison theorem
Cheng's eigenvalue comparison theorem
In Riemannian geometry, Cheng's eigenvalue comparison theorem states in general terms that when a domain is large, the first Dirichlet eigenvalue of its Laplace–Beltrami operator is small. This general characterization is not precise, in part because the notion of "size" of the domain must also...
. It is also known, by a result of Osgood, Phillips, and Sarnak that the moduli space of Riemann surfaces of a given genus does not admit a continuous isospectral flow through any point, and is compact in the Frechet–Schwartz topology.
Weyl's formula
Weyl's formula states that one can infer the area V of the drum by counting how rapidly the λn grow. We define N(R) to be the number of eigenvalues smaller than R and we get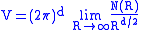
where d is the dimension. Weyl also conjectured that the next term in the approximation below would give the perimeter of D. In other words, if A denotes the length of the perimeter (or the surface area in higher dimension), then one should have
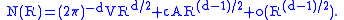
where c is some constant that depends only on the dimension. For smooth boundary, this was proved by V. Ja. Ivrii in 1980.
The Weyl–Berry conjecture
For non-smooth boundaries, Michael Berry conjectured in 1979 that the correction should be of the order of
where D is the Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
of the boundary. This was disproved by J. Brossard and R. A. Carmona, who then suggested one should replace the Hausdorff dimension with the upper box dimension. In the plane, this was proved if the boundary has dimension 1 (1993), but mostly disproved for higher dimensions (1996). Both results are by Lapidus and Pomerance
Carl Pomerance
Carl Bernard Pomerance is a well-known number theorist. He attended college at Brown University and later received his Ph.D. from Harvard University in 1972 with a dissertation proving that any odd perfect number has at least 7 distinct prime factors. He immediately joined the faculty at the...
.
External links
- Isospectral Drums by Toby Driscoll at the University of Delaware
- Some planar isospectral domains by Peter Buser, John Horton ConwayJohn Horton ConwayJohn Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
, Peter Doyle, and Klaus-Dieter Semmler - Drums That Sound Alike by Ivars Peterson at the Mathematical Association of America web site

