
Harmonic coordinate condition
Encyclopedia
The harmonic coordinate condition is one of several coordinate conditions
in general relativity
, which make it possible to solve the Einstein field equations
. A coordinate system is said to satisfy the harmonic coordinate condition if each of the coordinate functions xα (regarded as scalar fields) satisfies d'Alembert's equation
. The parallel notion of a harmonic coordinate system in Riemannian geometry
is a coordinate system whose coordinate functions satisfy Laplace's equation
. Since d'Alembert's equation
is the generalization of Laplace's equation to space-time, its solutions are also called "harmonic".
selects one (or a smaller set of) such coordinate system(s). The Cartesian coordinates used in special relativity satisfy d'Alembert's equation, so a harmonic coordinate system is the closest approximation available in general relativity to an inertial frame of reference in special relativity.
instead of the partial derivative in d'Alembert's equation, so we get:
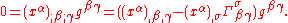
Since the coordinate xα is not actually a scalar, this is not a tensor equation. That is, it is not generally invariant. But coordinate conditions must not be generally invariant because they are supposed to pick out (only work for) certain coordinate systems and not others. Since the partial derivative of a coordinate is the Kronecker delta, we get:
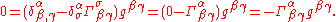
And thus, dropping the minus sign, we get the harmonic coordinate condition (also known as the de Donder
gauge ):
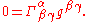
This condition is especially useful when working with gravitational waves.
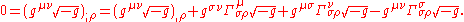
The last term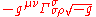 emerges because
emerges because  is not an invariant scalar, and so its covariant derivative is not the same as its ordinary derivative. Rather,
is not an invariant scalar, and so its covariant derivative is not the same as its ordinary derivative. Rather, 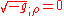 because
because 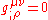 , while
, while 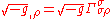 .
.
Contracting ν with ρ and applying the harmonic coordinate condition to the second term, we get:

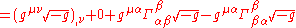
Thus, we get that an alternative way of expressing the harmonic coordinate condition is:
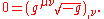

Let us evaluate the right hand side:

Using the harmonic coordinate condition we can eliminate the right-most term and then continue evaluation as follows:
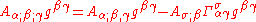

Coordinate conditions
In general relativity, the laws of physics can be expressed in a generally covariant form. In other words, the real world does not care about our coordinate systems. However, it is often useful to fix upon a particular coordinate system, in order to solve actual problems or make actual predictions...
in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, which make it possible to solve the Einstein field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
. A coordinate system is said to satisfy the harmonic coordinate condition if each of the coordinate functions xα (regarded as scalar fields) satisfies d'Alembert's equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
. The parallel notion of a harmonic coordinate system in Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
is a coordinate system whose coordinate functions satisfy Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
. Since d'Alembert's equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
is the generalization of Laplace's equation to space-time, its solutions are also called "harmonic".
Motivation
The laws of physics can be expressed in a generally invariant form. In other words, the real world does not care about our coordinate systems. However, for us to be able to solve the equations, we must fix upon a particular coordinate system. A coordinate conditionCoordinate conditions
In general relativity, the laws of physics can be expressed in a generally covariant form. In other words, the real world does not care about our coordinate systems. However, it is often useful to fix upon a particular coordinate system, in order to solve actual problems or make actual predictions...
selects one (or a smaller set of) such coordinate system(s). The Cartesian coordinates used in special relativity satisfy d'Alembert's equation, so a harmonic coordinate system is the closest approximation available in general relativity to an inertial frame of reference in special relativity.
Derivation
In general relativity, we have to use the covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
instead of the partial derivative in d'Alembert's equation, so we get:
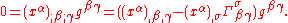
Since the coordinate xα is not actually a scalar, this is not a tensor equation. That is, it is not generally invariant. But coordinate conditions must not be generally invariant because they are supposed to pick out (only work for) certain coordinate systems and not others. Since the partial derivative of a coordinate is the Kronecker delta, we get:
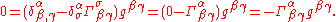
And thus, dropping the minus sign, we get the harmonic coordinate condition (also known as the de Donder
Théophile de Donder
Théophile Ernest de Donder was a Belgian mathematician and physicist famous for his 1923 work in developing correlations between the Newtonian concept of chemical affinity and the Gibbsian concept of free energy.-Education:...
gauge ):
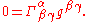
This condition is especially useful when working with gravitational waves.
Alternative form
Consider the covariant derivative of the density of the reciprocal of the metric tensor: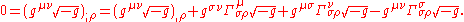
The last term
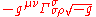 emerges because
emerges because  is not an invariant scalar, and so its covariant derivative is not the same as its ordinary derivative. Rather,
is not an invariant scalar, and so its covariant derivative is not the same as its ordinary derivative. Rather, 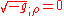 because
because 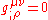 , while
, while 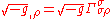 .
.Contracting ν with ρ and applying the harmonic coordinate condition to the second term, we get:

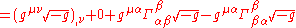
Thus, we get that an alternative way of expressing the harmonic coordinate condition is:
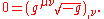
Effect on the wave equation
For example, consider the wave equation applied to the electromagnetic vector potential:
Let us evaluate the right hand side:

Using the harmonic coordinate condition we can eliminate the right-most term and then continue evaluation as follows:
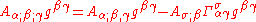

See also
- Christoffel symbolsChristoffel symbolsIn mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
- Covariant derivativeCovariant derivativeIn mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
- Gauge theoryGauge theoryIn physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
- General relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
- General covarianceGeneral covarianceIn theoretical physics, general covariance is the invariance of the form of physical laws under arbitrary differentiable coordinate transformations...
- Kronecker delta
- Laplace's equationLaplace's equationIn mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
- Laplace operatorLaplace operatorIn mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
- Wave equationWave equationThe wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
External links
- http://mathworld.wolfram.com/HarmonicCoordinates.html

