
Hamiltonian path
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a Hamiltonian path (or traceable path) is a path
Path (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
in an undirected graph that visits each vertex
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
exactly once. A Hamiltonian cycle (or Hamiltonian circuit) is a cycle
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
in an undirected graph that visits each vertex
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
exactly once and also returns to the starting vertex. Determining whether such paths and cycles exist in graphs is the Hamiltonian path problem
Hamiltonian path problem
In the mathematical field of graph theory the Hamiltonian path problem and the Hamiltonian cycle problem are problems of determining whether a Hamiltonian path or a Hamiltonian cycle exists in a given graph . Both problems are NP-complete...
, which is NP-complete.
Hamiltonian paths and cycles are named after William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
who invented the Icosian game
Icosian game
The icosian game is a mathematical game invented in 1857 by William Rowan Hamilton. The game's object is finding a Hamiltonian cycle along the edges of a dodecahedron such that every vertex is visited a single time, no edge is visited twice, and the ending point is the same as the starting point...
, now also known as Hamilton's puzzle, which involves finding a Hamiltonian cycle in the edge graph of the dodecahedron. Hamilton solved this problem using the Icosian Calculus
Icosian Calculus
The Icosian Calculus is a non-commutative algebraic structure discovered by the Irish mathematician William Rowan Hamilton in 1856.In modern terms, he gave a group presentation of the icosahedral rotation group by generators and relations....
, an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
based on roots of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
with many similarities to the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s (also invented by Hamilton). This solution does not generalize to arbitrary graphs. However, despite being named after Hamilton, Hamiltonian cycles in polyhedra had also been studied a year earlier by Thomas Kirkman.
Definitions
A Hamiltonian path or traceable path is a pathPath (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
that visits each vertex exactly once. A graph that contains a Hamiltonian path is called a traceable graph. A graph is Hamiltonian-connected if for every pair of vertices there is a Hamiltonian path between the two vertices.
A Hamiltonian cycle, Hamiltonian circuit, vertex tour or graph cycle is a cycle
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
that visits each vertex exactly once
(except the vertex that is both the start and end, and so is visited twice). A graph that contains a Hamiltonian cycle is called a Hamiltonian graph.
Similar notions may be defined for directed graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
s, where each edge (arc) of a path or cycle can only be traced in a single direction (i.e., the vertices are connected with arrows and the edges traced "tail-to-head").
A Hamiltonian decomposition is an edge decomposition of a graph into Hamiltonian circuits. This is one of the known but unsolved problems.
Examples
- a complete graphComplete graphIn the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
with more than two vertices is Hamiltonian - every cycle graphCycle graphIn graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
is Hamiltonian - every tournamentTournament (graph theory)A tournament is a directed graph obtained by assigning a direction for each edge in an undirected complete graph. That is, it is a directed graph in which every pair of vertices is connected by a single directed edge....
has an odd number of Hamiltonian paths - every platonic solidPlatonic solidIn geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
, considered as a graph, is Hamiltonian - every prismPrism (geometry)In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
is Hamiltonian - The Deltoidal hexecontahedronDeltoidal hexecontahedronIn geometry, a deltoidal hexecontahedron is a catalan solid which looks a bit like an overinflated dodecahedron. It is sometimes also called the trapezoidal hexecontahedron or strombic hexecontahedron...
is the only non-hamiltonian Archimedean dual - Every antiprismAntiprismIn geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
is Hamiltonian - A maximal planar graph with no separating triangles is Hamiltonian.
Properties
Any Hamiltonian cycle can be converted to a Hamiltonian path by removing one of its edges, but a Hamiltonian path can be extended to Hamiltonian cycle only if its endpoints are adjacent.The line graph
Line graph
In graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G...
of a Hamiltonian graph is Hamiltonian. The line graph of an Eulerian graph is Hamiltonian.
A tournament
Tournament (graph theory)
A tournament is a directed graph obtained by assigning a direction for each edge in an undirected complete graph. That is, it is a directed graph in which every pair of vertices is connected by a single directed edge....
(with more than 2 vertices) is Hamiltonian if and only if it is strongly connected
Strongly connected component
A directed graph is called strongly connected if there is a path from each vertex in the graph to every other vertex. In particular, this means paths in each direction; a path from a to b and also a path from b to a....
.
The problem of finding a Hamiltonian cycle may be used as the basis of a zero-knowledge proof.
The number of different Hamiltonian cycles in a complete undirected graph on
 vertices is
vertices is 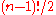 .
.The number of different Hamiltonian cycles in a complete directed graph on
 vertices is
vertices is  .
.Bondy–Chvátal theorem
The best vertex degree characterization of Hamiltonian graphs was provided in 1972 by the Bondy–ChvátalVáclav Chvátal
Václav Chvátal is a professor in the Department of Computer Science and Software Engineering at Concordia University in Montreal, Canada, where he holds theCanada Research Chair in Combinatorial Optimization....
theorem, which generalizes earlier results by G. A. Dirac
Gabriel Andrew Dirac
Gabriel Andrew Dirac was a mathematician who mainly worked in graph theory. He stated a sufficient condition for a graph to contain a Hamiltonian circuit.Dirac received his Ph.D...
(1952) and Øystein Ore
Øystein Ore
Øystein Ore was a Norwegian mathematician.-Life:Ore was graduated from the University of Oslo in 1922, with a Cand.Scient. degree in mathematics. In 1924, the University of Oslo awarded him the Ph.D. for a thesis titled Zur Theorie der algebraischen Körper, supervised by Thoralf Skolem...
. In fact, both Dirac's and Ore's theorems are less powerful than what can be derived from Pósa
Lajos Pósa (mathematician)
Lajos Pósa is a Hungarian mathematician, working in combinatorics. Paul Erdős's favorite "child", he discovered theorems at the age of 16. Since 2002 he works at the Rényi Institute of the Hungarian Academy of Sciences; earlier he was at the Eötvös Loránd University, at the Departments of...
's theorem (1962). Dirac and Ore's theorems basically state that a graph is Hamiltonian if it has enough edges. First we have to define the closure of a graph.
Given a graph G with n vertices, the closure cl(G) is uniquely constructed from G by successively adding for all nonadjacent pairs of vertices u and v with degree(v) + degree(u) ≥ n the new edge uv.
Bondy–Chvátal theorem
- A graph is Hamiltonian if and only if its closure is Hamiltonian.
As complete graphs are Hamiltonian, all graphs whose closure is complete are Hamiltonian, which is the content of the following earlier theorems by Dirac and Ore.
Dirac (1952)
- A simple graph with n vertices (n ≥ 3) is Hamiltonian if each vertex has degree n/2 or greater.
Ore (1960)
- A graph with n vertices (n ≥ 3) is Hamiltonian if, for each pair of non-adjacent vertices, the sum of their degrees is n or greater (see Ore's theoremOre's theoremOre's theorem is a result in graph theory proved in 1960 by Norwegian mathematician Øystein Ore. It gives a sufficient condition for a graph to be Hamiltonian, essentially stating that a graph with "sufficiently many edges" must contain a Hamilton cycle...
).
The following theorems can be regarded as directed versions:
Ghouila-Houiri (1960)
- A strongly connected simple directed graphDirected graphA directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
with n vertices is Hamiltonian if some vertex has a full degree smaller than n.
Meyniel (1973)
- A strongly connected simple directed graphDirected graphA directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
with n vertices is Hamiltonian if the sum of full degrees of some two distinct non-adjacent vertices is smaller than 2n − 1.
The number of vertices must be doubled because each undirected edge corresponds to two directed arcs and thus the degree of a vertex in the directed graph is twice the degree in the undirected graph.
See also
- Barnette's conjectureBarnette's conjectureBarnette's conjecture is an unsolved problem in graph theory, a branch of mathematics, concerning Hamiltonian cycles in graphs. It is named after David W...
, an open problem on Hamiltonicity of cubic bipartiteBipartite graphIn the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
polyhedral graphPolyhedral graphIn polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
s - Eulerian pathEulerian pathIn graph theory, an Eulerian trail is a trail in a graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is a Eulerian trail which starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of...
, a path through all edges in a graph - Grinberg's theoremGrinberg's theoremIn graph theory, Grinberg's theorem is a necessary condition on the planar graph to contain a Hamiltonian cycle. The result has been widely used to construct non-Hamiltonian planar graphs with further properties, such as to give new counterexamples to Tait's conjecture...
giving a necessary condition for planar graphPlanar graphIn graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s to have a Hamiltonian cycle - Knight's tourKnight's tourThe knight's tour is a mathematical problem involving a knight on a chessboard. The knight is placed on the empty board and, moving according to the rules of chess, must visit each square exactly once. A knight's tour is called a closed tour if the knight ends on a square attacking the square from...
, a Hamiltonian cycle in the knight's graph - Hamiltonian path problemHamiltonian path problemIn the mathematical field of graph theory the Hamiltonian path problem and the Hamiltonian cycle problem are problems of determining whether a Hamiltonian path or a Hamiltonian cycle exists in a given graph . Both problems are NP-complete...
, the computational problem of finding Hamiltonian paths - Hypohamiltonian graphHypohamiltonian graphIn the mathematical field of graph theory, a graph G is said to be hypohamiltonian if G does not itself have a Hamiltonian cycle but every graph formed by removing a single vertex from G is Hamiltonian.-History:...
, a non-Hamiltonian graph in which every vertex-deleted subgraph is Hamiltonian - LCF notationLCF notationIn combinatorial mathematics, LCF notation or LCF code is a notation devised by Joshua Lederberg, and extended by Coxeter and Frucht, for the representation of cubic graphs that are Hamiltonian. Since the graphs are Hamiltonian, the vertices can be arranged in a cycle, which accounts for two edges...
for Hamiltonian cubic graphCubic graphIn the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
s. - Lovász conjectureLovász conjectureIn graph theory, the Lovász conjecture is a classical problem on Hamiltonian paths in graphs. It says:The original article of Lovász stated the result in the opposite, butthis version became standard...
that vertex-transitive graphVertex-transitive graphIn the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
s are Hamiltonian - Pancyclic graphPancyclic graphIn the mathematical study of graph theory, a pancyclic graph is a directed or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph...
, graphs with cycles of all lengths including a Hamiltonian cycle - Snake-in-the-boxSnake-in-the-boxThe snake-in-the-box problem in graph theory and computer science deals with finding a certain kind of path along the edges of a hypercube. This path starts at one corner and travels along the edges to as many corners as it can reach. After it gets to a new corner, the previous corner and all of...
, the longest induced pathInduced pathIn the mathematical area of graph theory, an induced path in an undirected graph G is a path that is an induced subgraph of G. That is, it is a sequence of vertices in G such that each two adjacent vertices in the sequence are connected by an edge in G, and each two nonadjacent vertices in the...
in a hypercube - Steinhaus–Johnson–Trotter algorithm for finding a Hamiltonian path in a permutohedronPermutohedronIn mathematics, the permutohedron of order n is an -dimensional polytope embedded in an n-dimensional space, the vertices of which are formed by permuting the coordinates of the vector .-History:According to , permutohedra were first studied by...
- Tait's conjectureTait's conjectureIn mathematics, Tait's conjecture states that "Every 3-connected planar cubic graph has a Hamiltonian cycle through all its vertices". It was proposed by and disproved by , who constructed a counterexample with 25 faces, 69 edges and 46 vertices...
(now known false) that 3-regular polyhedral graphPolyhedral graphIn polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
s are Hamiltonian - Travelling salesman problemTravelling salesman problemThe travelling salesman problem is an NP-hard problem in combinatorial optimization studied in operations research and theoretical computer science. Given a list of cities and their pairwise distances, the task is to find the shortest possible tour that visits each city exactly once...

