Hamilton's principle
Encyclopedia
In physics
, Hamilton's principle is William Rowan Hamilton
's formulation of the principle of stationary action (see that article for historical formulations). It states that the dynamics of a physical system is determined by a variational problem
for a functional based on a single function, the Lagrangian
, which contains all physical information concerning the system and the forces acting on it. The variational problem is equivalent to and allows for the derivation of the differential
equations of motion of the physical system. Although formulated originally for classical mechanics
, Hamilton's principle also applies to classical fields
such as the electromagnetic
and gravitational fields
, and has even been extended to quantum mechanics
, quantum field theory
and criticality theories.
of a system described by 
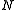generalized coordinates
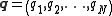between two specified states 
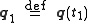and 
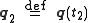at two specified times 
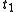and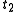 
is a stationary point
(a point where the variation
is zero), of the action
functional
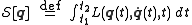
where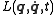
is the Lagrangian
function
for the system. In other words, any first-order perturbation of the true evolution results in (at most) second-order changes in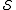
. The action 
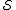is a functional
, i.e., something that takes as its input a function
and returns a single number, a scalar
. In terms of functional analysis
, Hamilton's principle states that the true evolution of a physical system is a solution of the functional equation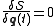
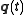be a stationary point
of the action
functional
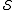is equivalent to a set of differential equations for 
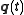(the Euler-Lagrange equations), which may be derived as follows.
Let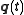
represent the true evolution of the system between two specified states 
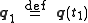and 
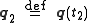at two specified times 
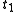and 
, and let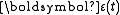 
be a small perturbation that is zero at the endpoints of the trajectory
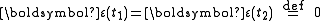
To first order in the perturbation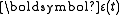
, the change in the action functional 
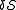would be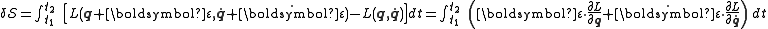
where we have expanded the Lagrangian
L to first order in the perturbation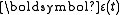
.
Applying integration by parts
to the last term results in
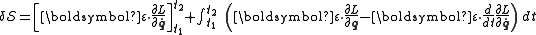
The boundary conditions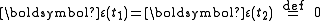
causes the first term to vanish
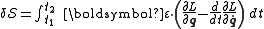
Hamilton's principle requires that this first-order change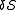
is zero for all possible perturbations 
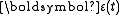, i.e., the true path is a stationary point
of the action functional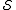
(either a minimum, maximum or saddle point). This requirement can be satisfied if and only if
These equations are called the Euler-Lagrange equations for the variational problem.
The conjugate momentum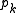
for a generalized coordinate 
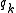is defined by the equation 
.
An important special case of these equations occurs when L does not contain a generalized coordinate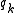
explicitly, i.e.,
In such cases, the coordinate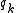
is called a cyclic coordinate. For example, if we use polar coordinates t, r, θ to describe the planar motion of a particle, and if L does not depend on θ, the conjugate momentum is the conserved angular momentum.
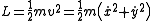
in orthonormal (x,y) coordinates, where the dot represents differentiation with respect to the curve parameter (usually the time, t). Therefore, upon application of the Euler-Lagrange equations,
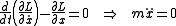
And likewise for y. Thus the Euler-Lagrange formulation can be used to derive Newton's laws.
In polar coordinates (r, φ) the kinetic energy and hence the Lagrangian becomes
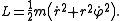
The radial r and φ components of the Euler-Lagrangian equations become, respectively
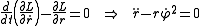
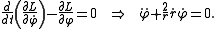
The solution of these two equations is given by
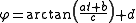
for a set of constants a, b, c, d determined by initial conditions.
Thus, indeed, the solution is a straight line given in polar coordinates: a is the velocity, c is the distance of the closest approach to the origin, and d is the angle of motion.
are occasionally confused and both have been called (incorrectly) the principle of least action
. They differ in three important ways:
, such as the electromagnetic field
or gravity
.
The Einstein equation utilizes the Einstein-Hilbert action
as constrained by a variational principle
.
The path of a body in a gravitational field (i.e. free fall in space time, a so called geodesic) can be found using the action principle.
. As opposed to a system composed of rigid bodies, deformable bodies have an infinite number of degrees of freedom and occupy continuous regions of space; consequently, the state of the system is described by using continuous functions of space and time. The extended Hamilton Principle for such bodies is given by
where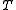
is the kinetic energy, 
is the elastic energy,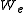 
is the work done by
external loads on the body, and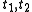
the initial and final times. If the system is conservative, the work done by external forces may be derived from a scalar potential 
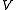. In this case,
This is called Hamilton's principle and it is invariant under coordinate transformations.
, the system does not follow a single path whose action is stationary, but the behavior of the system depends on all imaginable paths and the value of their action. The action corresponding to the various paths is used to calculate the path integral
, that gives the probability amplitude
s of the various outcomes.
Although equivalent in classical mechanics with Newton's laws, the action principle is better suited for generalizations and plays an important role in modern physics. Indeed, this principle is one of the great generalizations in physical science. In particular, it is fully appreciated and best understood within quantum mechanics
. Richard Feynman
's path integral formulation
of quantum mechanics is based on a stationary-action principle, using path integrals. Maxwell's equations
can be derived as conditions of stationary action.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, Hamilton's principle is William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
's formulation of the principle of stationary action (see that article for historical formulations). It states that the dynamics of a physical system is determined by a variational problem
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
for a functional based on a single function, the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
, which contains all physical information concerning the system and the forces acting on it. The variational problem is equivalent to and allows for the derivation of the differential
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
equations of motion of the physical system. Although formulated originally for classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, Hamilton's principle also applies to classical fields
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
such as the electromagnetic
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
and gravitational fields
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
, and has even been extended to quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
and criticality theories.
Mathematical formulation
Hamilton's principle states that the true evolution of a system described by 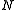generalized coordinatesGeneralized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
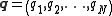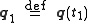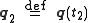between two specified states and at two specified times 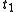and 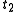is a stationary pointStationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
(a point where the variation
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
is zero), of the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
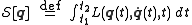
where
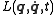is the LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
for the system. In other words, any first-order perturbation of the true evolution results in (at most) second-order changes in
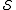. The action 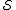is a functionalFunctional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
, i.e., something that takes as its input a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
and returns a single number, a scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
. In terms of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, Hamilton's principle states that the true evolution of a physical system is a solution of the functional equation
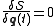
Euler-Lagrange equations for the action integral
Requiring that the true trajectory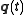 be a stationary pointStationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
of the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
functional
Functional
Generally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...
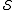is equivalent to a set of differential equations for 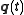(the Euler-Lagrange equations), which may be derived as follows.Let
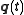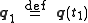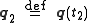represent the true evolution of the system between two specified states and at two specified times 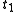and , and let 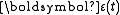be a small perturbation that is zero at the endpoints of the trajectory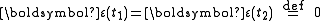To first order in the perturbation
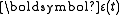, the change in the action functional 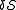would be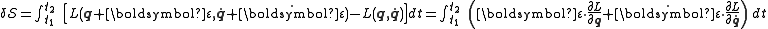where we have expanded the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
L to first order in the perturbation
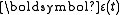.Applying integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
to the last term results in
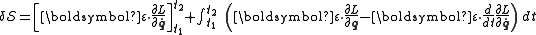
The boundary conditions
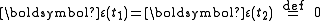causes the first term to vanish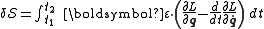Hamilton's principle requires that this first-order change
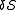is zero for all possible perturbations 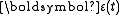, i.e., the true path is a stationary pointStationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
of the action functional
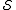(either a minimum, maximum or saddle point). This requirement can be satisfied if and only ifThese equations are called the Euler-Lagrange equations for the variational problem.
The conjugate momentum
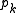for a generalized coordinate 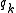is defined by the equation .An important special case of these equations occurs when L does not contain a generalized coordinate
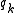explicitly, i.e.,- if
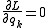, the conjugate momentum 
is constant.
In such cases, the coordinate
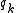is called a cyclic coordinate. For example, if we use polar coordinates t, r, θ to describe the planar motion of a particle, and if L does not depend on θ, the conjugate momentum is the conserved angular momentum.Example: Free particle in polar coordinates
Trivial examples help to appreciate the use of the action principle via the Euler-Lagrangian equations. A free particle (mass m and velocity v) in Euclidean space moves in a straight line. Using the Euler-Lagrange equations, this can be shown in polar coordinates as follows. In the absence of a potential, the Lagrangian is simply equal to the kinetic energy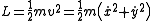in orthonormal (x,y) coordinates, where the dot represents differentiation with respect to the curve parameter (usually the time, t). Therefore, upon application of the Euler-Lagrange equations,
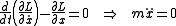
And likewise for y. Thus the Euler-Lagrange formulation can be used to derive Newton's laws.
In polar coordinates (r, φ) the kinetic energy and hence the Lagrangian becomes
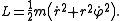
The radial r and φ components of the Euler-Lagrangian equations become, respectively
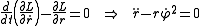
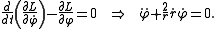
The solution of these two equations is given by
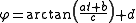
for a set of constants a, b, c, d determined by initial conditions.
Thus, indeed, the solution is a straight line given in polar coordinates: a is the velocity, c is the distance of the closest approach to the origin, and d is the angle of motion.
Comparison with Maupertuis' principle
Hamilton's principle and Maupertuis' principleMaupertuis' principle
In classical mechanics, Maupertuis' principle is an integral equation that determines the path followed by a physical system without specifying the time parameterization of that path. It is a special case of the more generally stated principle of least action...
are occasionally confused and both have been called (incorrectly) the principle of least action
Principle of least action
In physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
. They differ in three important ways:
- their definition of the actionAction (physics)In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
...
-
-
- Maupertuis' principle uses an integral over the generalized coordinatesGeneralized coordinatesIn the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
known as the abbreviated action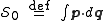
where 
are the conjugate momenta defined above. By contrast, Hamilton's principle uses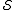 
, the integral of the LagrangianLagrangianThe Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
over timeTimeTime is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
.
- Maupertuis' principle uses an integral over the generalized coordinates
-
- the solution that they determine...
-
-
- Hamilton's principle determines the trajectory
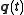as a function of time, whereas Maupertuis' principle determines only the shape of the trajectory in the generalized coordinates. For example, Maupertuis' principle determines the shape of the ellipse on which a particle moves under the influence of an inverse-square central force such as gravityGravitationGravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
, but does not describe per se how the particle moves along that trajectory. (However, this time parameterization may be determined from the trajectory itself in subsequent calculations using the conservation of energy.) By contrast, Hamilton's principle directly specifies the motion along the ellipse as a function of time.
- Hamilton's principle determines the trajectory
-
- ...and the constraints on the variation.
-
-
- Maupertuis' principle requires that the two endpoint states
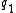and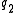 
be given and that energy be conserved along every trajectory. By contrast, Hamilton's principle does not require the conservation of energy, but does require that the endpoint times 
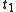and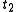 
be specified as well as the endpoint states 
and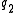 
.
- Maupertuis' principle requires that the two endpoint states
-
Action principle for classical fields
The action principle can be extended to obtain the equations of motion for fieldsField (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
, such as the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
or gravity
Einstein-Hilbert action
The Einstein–Hilbert action in general relativity is the action that yields the Einstein's field equations through the principle of least action...
.
The Einstein equation utilizes the Einstein-Hilbert action
Einstein-Hilbert action
The Einstein–Hilbert action in general relativity is the action that yields the Einstein's field equations through the principle of least action...
as constrained by a variational principle
Variational principle
A variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
.
The path of a body in a gravitational field (i.e. free fall in space time, a so called geodesic) can be found using the action principle.
Hamilton's principle applied to deformable bodies
Hamilton's principle is an important variational principle in elastodynamicsLinear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
. As opposed to a system composed of rigid bodies, deformable bodies have an infinite number of degrees of freedom and occupy continuous regions of space; consequently, the state of the system is described by using continuous functions of space and time. The extended Hamilton Principle for such bodies is given by
where
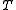is the kinetic energy, is the elastic energy, 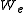is the work done byexternal loads on the body, and
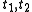the initial and final times. If the system is conservative, the work done by external forces may be derived from a scalar potential 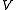. In this case,
This is called Hamilton's principle and it is invariant under coordinate transformations.
Action principle in quantum mechanics and quantum field theory
In quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the system does not follow a single path whose action is stationary, but the behavior of the system depends on all imaginable paths and the value of their action. The action corresponding to the various paths is used to calculate the path integral
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
, that gives the probability amplitude
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
s of the various outcomes.
Although equivalent in classical mechanics with Newton's laws, the action principle is better suited for generalizations and plays an important role in modern physics. Indeed, this principle is one of the great generalizations in physical science. In particular, it is fully appreciated and best understood within quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
's path integral formulation
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
of quantum mechanics is based on a stationary-action principle, using path integrals. Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
can be derived as conditions of stationary action.