
Halley's method
Encyclopedia
In numerical analysis
, Halley’s method is a root-finding algorithm
used for functions of one real variable with a continuous second derivative, i.e., C2 functions. It is named after its inventor Edmond Halley
, who also discovered Halley's Comet.
The algorithm is second in the class of Householder's method
s, right after Newton's method
. Like the latter, it produces iteratively a sequence of approximations to the root; their rate of convergence
to the root is cubic. Multidimensional versions of this method exist.
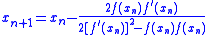
beginning with an initial guess x0.
If ƒ is a three times continuously differentiable function and a is a zero of ƒ but not of its derivative, then, in a neighborhood of a, the iterates xn satisfy:
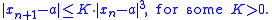
This means that the iterates converge to the zero if the initial guess is sufficiently close, and that the convergence is cubic.
The following alternative formulation shows the similarity between Halley’s method and Newton’s method. The expression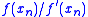 is computed only once, and it is particularly useful when
is computed only once, and it is particularly useful when 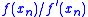 can be simplified.
can be simplified.
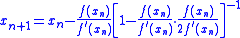
A further alternative is as below, in which case the technique is sometimes referred to as Bailey’s method.
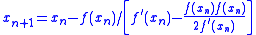
Using any variation, when the second derivative
is very close to zero, the iteration is almost the same as under Newton’s method.

Any root of ƒ which is not a root of its derivative is a root of g; and any root of g is a root of ƒ. Applying Newton's method
to g gives
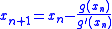
with
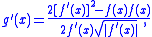
and the result follows. Notice that if ƒ'(c) = 0, then one cannot apply this at c because g(c) would be undefined.
implies:
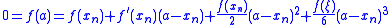
and also
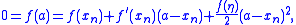
where ξ and η are numbers lying between a and xn. Multiply the first equation by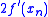 and subtract from it the second equation times
and subtract from it the second equation times 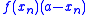 to give:
to give:
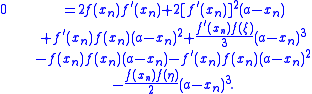
Canceling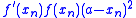 and re-organizing terms yields:
and re-organizing terms yields:
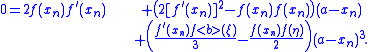
Put the second term on the left side and divide through by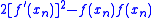 to get:
to get:
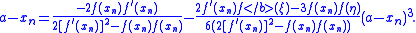
Thus:
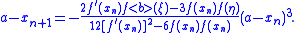
The limit of the coefficient on the right side as xn approaches a is:

If we take K to be a little larger than the absolute value of this, we can take absolute values of both sides of the formula and replace the absolute value of coefficient by its upper bound near a to get:
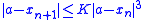
which is what was to be proved.
To summarize,
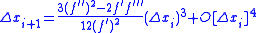 ,
,
where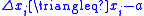 .
.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, Halley’s method is a root-finding algorithm
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
used for functions of one real variable with a continuous second derivative, i.e., C2 functions. It is named after its inventor Edmond Halley
Edmond Halley
Edmond Halley FRS was an English astronomer, geophysicist, mathematician, meteorologist, and physicist who is best known for computing the orbit of the eponymous Halley's Comet. He was the second Astronomer Royal in Britain, following in the footsteps of John Flamsteed.-Biography and career:Halley...
, who also discovered Halley's Comet.
The algorithm is second in the class of Householder's method
Householder's method
In numerical analysis, the class of Householder's methods are root-finding algorithms used for functions of one real variable with continuous derivatives up to some order d+1, where d will be the order of the Householder's method....
s, right after Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
. Like the latter, it produces iteratively a sequence of approximations to the root; their rate of convergence
Rate of convergence
In numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
to the root is cubic. Multidimensional versions of this method exist.
Method
Like any root-finding method, Halley’s method is a numerical algorithm for solving the nonlinear equation ƒ(x) = 0. In this case, the function ƒ has to be a function of one real variable. The method consists of a sequence of iterations: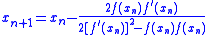
beginning with an initial guess x0.
If ƒ is a three times continuously differentiable function and a is a zero of ƒ but not of its derivative, then, in a neighborhood of a, the iterates xn satisfy:
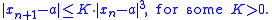
This means that the iterates converge to the zero if the initial guess is sufficiently close, and that the convergence is cubic.
The following alternative formulation shows the similarity between Halley’s method and Newton’s method. The expression
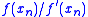 is computed only once, and it is particularly useful when
is computed only once, and it is particularly useful when 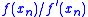 can be simplified.
can be simplified.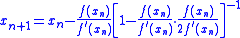
A further alternative is as below, in which case the technique is sometimes referred to as Bailey’s method.
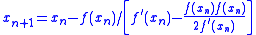
Using any variation, when the second derivative
Second derivative
In calculus, the second derivative of a function ƒ is the derivative of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is...
is very close to zero, the iteration is almost the same as under Newton’s method.
Derivation
Consider the function
Any root of ƒ which is not a root of its derivative is a root of g; and any root of g is a root of ƒ. Applying Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
to g gives
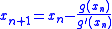
with
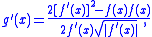
and the result follows. Notice that if ƒ'(c) = 0, then one cannot apply this at c because g(c) would be undefined.
Cubic convergence
Suppose a is a root of f but not of its derivative. And suppose that the third derivative of f exists and is continuous in a neighborhood of a and xn is in that neighborhood. Then Taylor's theoremTaylor's theorem
In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
implies:
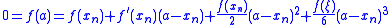
and also
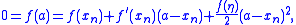
where ξ and η are numbers lying between a and xn. Multiply the first equation by
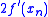 and subtract from it the second equation times
and subtract from it the second equation times 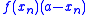 to give:
to give: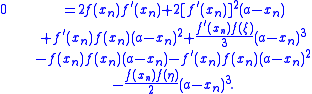
Canceling
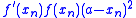 and re-organizing terms yields:
and re-organizing terms yields: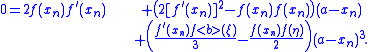
Put the second term on the left side and divide through by
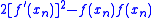 to get:
to get: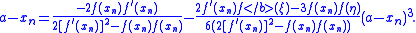
Thus:
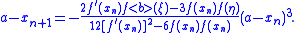
The limit of the coefficient on the right side as xn approaches a is:

If we take K to be a little larger than the absolute value of this, we can take absolute values of both sides of the formula and replace the absolute value of coefficient by its upper bound near a to get:
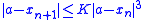
which is what was to be proved.
To summarize,
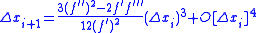 ,
,where
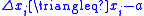 .
.External links
- Halley's Method by John H. Mathews
- Halley's Method by P. J. Acklam
- Newton's method and high order iterations, Pascal Sebah and Xavier Gourdon, 2001 (the site has a link to a Postscript version for better formula display)

