Green's function (many-body theory)
Encyclopedia
In many-body theory
, the term Green's function (or Green function) is sometimes used interchangeably with correlation function
, but refers specifically to correlators of field operators or creation and annihilation operators
.
The name comes from the Green's functions used to solve inhomogeneous differential equations, to which they are loosely related. (Specifically, only two-point 'Green's functions' are Green's functions in the mathematical sense; the linear operator that they invert is the part of the Hamiltonian operator
that is quadratic in the fields.)
.
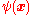The Heisenberg operators
can be written in terms of Schrödinger operators
as
and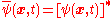
, where 
is the grand-canonical
Hamiltonian.
Similarly, for the imaginary-time
operators,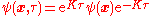
(Note that the imaginary-time creation operator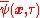
is not the Hermitian conjugate of the annihilation operator 
.)
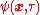In real time, the
-point Green function is defined by
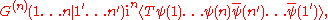
where we have used a condensed notation in which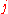
signifies 
and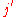 
signifies 
. The operator 
denotes time ordering, and indicates that the field operators that follow it are to be ordered so that the their time arguments increase from right to left.
In imaginary time, the corresponding definition is
where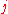
signifies 
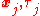. (The imaginary-time variables 
are restricted to the range 
to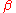 
.)
Note regarding signs and normalization used in these definitions: The signs of the Green functions have been chosen so that Fourier transform
of the two-point (
) thermal Green function for a free particle is
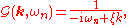
and the retarded Green function is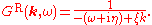
(See below for details.)
Throughout,
is 
for boson
s and
for fermion
s and
denotes either a commutator
or anticommutator as appropriate.
) is referred to as the two-point function, or propagator. In the presence of both spatial and temporal translational symmetry, it depends only on the difference of its arguments. Taking the Fourier transform with respect to both space and time gives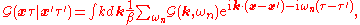
where the sum is over the appropriate Matsubara frequencies (and the integral involves an implicit factor of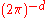
, as usual).
In real time, we will explicitly indicate the time-ordered function with a superscript T: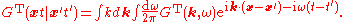
The real-time two-point Green function can be written in terms of `retarded' and `advanced' Green functions, which will turn out to have simpler analyticity properties. The retarded and advanced Green functions are defined by
and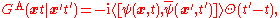
respectively.
They are related to the time-ordered Green function by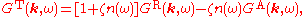
where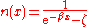
is the Bose-Einstein or Fermi-Dirac distribution function.
Imaginary-time ordering and
The thermal Green functions are defined only when both imaginary-time arguments are within the range 
to 
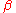. The two-point Green function has the following properties. (The position or momentum arguments are suppressed in this section.)
Firstly, it depends only on the difference of the imaginary times:
The argument
is allowed to run from 
to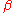 
.
Secondly,
is periodic under shifts of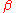 
. Because of the small domain within which the function is defined, this means just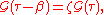
for
. (Note that the function is antiperiodic for fermions.) Time ordering is crucial for this property, which can be proved straightforwardly, using the cyclicity of the trace operation.
These two properties allow for the Fourier transform representation and its inverse,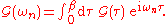
Finally, note that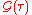
has a discontinuity at 
; this is consistent with a long-distance behaviour of 
.
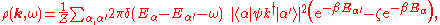
where
refers to a (many-body) eigenstate of the grand-canonical Hamiltonian 
, with eigenvalue 
.
The imaginary-time propagator is then given by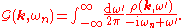
and the retarded propagator by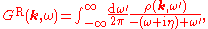
where the limit as
is implied.
The advanced propagator is given by the same expression, but with
in the denominator. The time-ordered function can be found in terms of 
and 
. As claimed above, 
and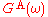 
have simple analyticity properties: the former (latter) has all its poles and discontinuities in the lower (upper) half-plane. The thermal propagator 
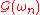has all its poles and discontinuities on the imaginary 
axis.
The spectral density can be found very straightforwardly from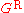
, using the Sokhatsky–Weierstrass theorem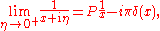
where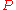
denotes the Cauchy principal part.
This gives
This furthermore implies that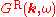
obeys the following relationship between its real and imaginary parts:
where
denotes the principal value of the integral.
The spectral density obeys a sum rule: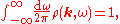
which gives
as
.
which is related to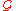
and 
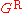by
and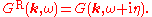
A similar expression obviously holds for
.
The relation between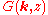
and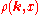 
is referred to as a Hilbert transform
.
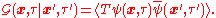
Due to translational symmetry, it is only necessary to consider
for 
, given by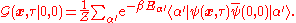
Inserting a complete set of eigenstates gives
Since
and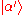 
are eigenstates of 
, the Heisenberg operators can be rewritten in terms of Schrödinger operators, giving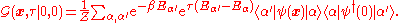
Performing the Fourier transform then gives
Momentum conservation allows the final term to be written as (up to possible factors of the volume)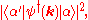
which confirms the expressions for the Green functions in the spectral representation.
The sum rule can be proved by considering the expectation value of the commutator,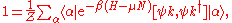
and then inserting a complete set of eigenstates into both terms of the commutator:
Swapping the labels in the first term then gives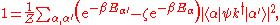
which is exactly the result of the integration of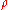
.
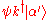is an eigenstate with (grand-canonical) energy 
, where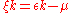 
is the single-particle dispersion relation measured with respect to the chemical potential. The spectral density therefore becomes
From the commutation relations,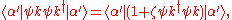
with possible factors of the volume again. The sum, which involves the thermal average of the number operator, then gives simply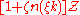
, leaving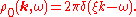
The imaginary-time propagator is thus
and the retarded propagator is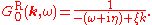
, the spectral density becomes
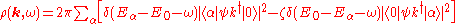
where
corresponds to the ground state. Note that only the first (second) term contributes when 
is positive (negative).
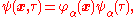
where
is the annihilation operator for the single-particle state 
and 
is that state's wavefunction in the position basis. This gives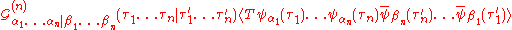
with a similar expression for
.
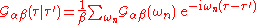
and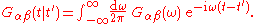
We can again define retarded and advanced functions in the obvious way; these are related to the time-ordered function in the same way as above.
The same periodicity properties as described in above apply to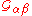
. Specifically,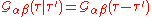
and
for
.
where
and 
are many-body states.
The expressions for the Green functions are modified in the obvious ways: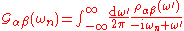
and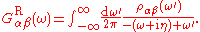
Their analyticity properties are identical. The proof follows exactly the same steps, except that the two matrix elements are no longer complex conjugates.
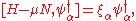
then for
an eigenstate:
so is
:
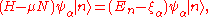
and so is
:
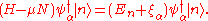
We therefore have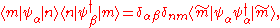
where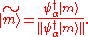
We then rewrite
and use the fact that the thermal average of the number operator gives the Bose-Einstein or Fermi-Dirac distribution function.
Finally, the spectral density simplifies to give
so that the thermal Green function is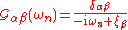
and the retarded Green function is
Note that the noninteracting Green function is diagonal, but this will not be true in the interacting case.
Many-body theory
The many-body theory is an area of physics which provides the framework for understanding the collective behavior of vast assemblies of interacting particles. In general terms, the many-body theory deals with effects that manifest themselves only in systems containing large numbers of constituents...
, the term Green's function (or Green function) is sometimes used interchangeably with correlation function
Correlation function (quantum field theory)
In quantum field theory, the matrix element computed by inserting a product of operators between two states, usually the vacuum states, is called a correlation function....
, but refers specifically to correlators of field operators or creation and annihilation operators
Creation and annihilation operators
Creation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
.
The name comes from the Green's functions used to solve inhomogeneous differential equations, to which they are loosely related. (Specifically, only two-point 'Green's functions' are Green's functions in the mathematical sense; the linear operator that they invert is the part of the Hamiltonian operator
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
that is quadratic in the fields.)
Basic definitions
We consider a many-body theory with field operator (annihilation operator written in the position basis)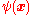.The Heisenberg operators
Heisenberg picture
In physics, the Heisenberg picture is a formulation of quantum mechanics in which the operators incorporate a dependency on time, but the state vectors are time-independent. It stands in contrast to the Schrödinger picture in which the operators are constant and the states evolve in time...
can be written in terms of Schrödinger operators
Schrödinger picture
In physics, the Schrödinger picture is a formulation of quantum mechanics in which the state vectors evolve in time, but the operators are constant. This differs from the Heisenberg picture which keeps the states constant while the observables evolve in time...
as
and
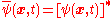, where is the grand-canonicalGrand canonical ensemble
In statistical mechanics, a grand canonical ensemble is a theoretical collection of model systems put together to mirror the calculated probability distribution of microscopic states of a given physical system which is being maintained in a given macroscopic state...
Hamiltonian.
Similarly, for the imaginary-time
Imaginary time
Imaginary time is a concept derived from quantum mechanics and is essential in connecting quantum mechanics with statistical mechanics.- In quantum mechanics :...
operators,
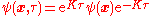
(Note that the imaginary-time creation operator
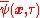is not the Hermitian conjugate of the annihilation operator 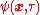.)In real time, the
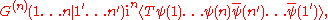
-point Green function is defined bywhere we have used a condensed notation in which
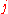signifies and 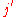signifies . The operator denotes time ordering, and indicates that the field operators that follow it are to be ordered so that the their time arguments increase from right to left.In imaginary time, the corresponding definition is
where
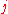signifies 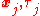. (The imaginary-time variables are restricted to the range to 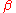.)Note regarding signs and normalization used in these definitions: The signs of the Green functions have been chosen so that Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the two-point (
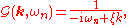
) thermal Green function for a free particle isand the retarded Green function is
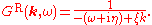
(See below for details.)
Throughout,
is for bosonBoson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s and
for fermionFermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s and
denotes either a commutatorCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
or anticommutator as appropriate.
Two-point functions
The Green function with a single pair of arguments () is referred to as the two-point function, or propagator. In the presence of both spatial and temporal translational symmetry, it depends only on the difference of its arguments. Taking the Fourier transform with respect to both space and time gives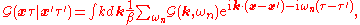where the sum is over the appropriate Matsubara frequencies (and the integral involves an implicit factor of
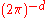, as usual).In real time, we will explicitly indicate the time-ordered function with a superscript T:
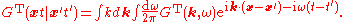
The real-time two-point Green function can be written in terms of `retarded' and `advanced' Green functions, which will turn out to have simpler analyticity properties. The retarded and advanced Green functions are defined by
and
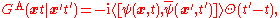
respectively.
They are related to the time-ordered Green function by
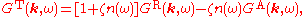
where
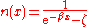
is the Bose-Einstein or Fermi-Dirac distribution function.
Imaginary-time ordering and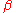 
-periodicity
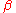The thermal Green functions are defined only when both imaginary-time arguments are within the range to . The two-point Green function has the following properties. (The position or momentum arguments are suppressed in this section.)Firstly, it depends only on the difference of the imaginary times:
The argument
is allowed to run from to 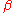.Secondly,
is periodic under shifts of 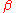. Because of the small domain within which the function is defined, this means just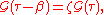for
. (Note that the function is antiperiodic for fermions.) Time ordering is crucial for this property, which can be proved straightforwardly, using the cyclicity of the trace operation.These two properties allow for the Fourier transform representation and its inverse,
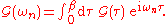
Finally, note that
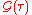has a discontinuity at ; this is consistent with a long-distance behaviour of .Spectral representation
The propagators in real and imaginary time can both be related to the spectral density (or spectral weight), given by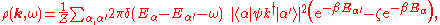where
refers to a (many-body) eigenstate of the grand-canonical Hamiltonian , with eigenvalue .The imaginary-time propagator is then given by
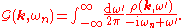
and the retarded propagator by
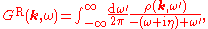
where the limit as
is implied.The advanced propagator is given by the same expression, but with
in the denominator. The time-ordered function can be found in terms of and . As claimed above, and 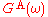have simple analyticity properties: the former (latter) has all its poles and discontinuities in the lower (upper) half-plane. The thermal propagator 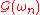has all its poles and discontinuities on the imaginary axis.The spectral density can be found very straightforwardly from
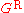, using the Sokhatsky–Weierstrass theorem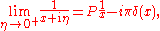where
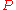denotes the Cauchy principal part.This gives
This furthermore implies that
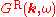obeys the following relationship between its real and imaginary parts:where
denotes the principal value of the integral.The spectral density obeys a sum rule:
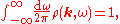
which gives
as
.Hilbert transform
The similarity of the spectral representations of the imaginary- and real-time Green functions allows us to define the functionwhich is related to
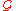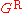and byand
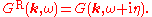
A similar expression obviously holds for
.The relation between
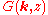and 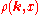is referred to as a Hilbert transformHilbert transform
In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the...
.
Proof of spectral representation
We demonstrate the proof of the spectral representation of the propagator in the case of the thermal Green function, defined as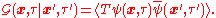Due to translational symmetry, it is only necessary to consider
for , given by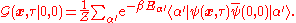Inserting a complete set of eigenstates gives
Since
and 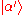are eigenstates of , the Heisenberg operators can be rewritten in terms of Schrödinger operators, giving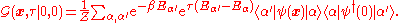Performing the Fourier transform then gives
Momentum conservation allows the final term to be written as (up to possible factors of the volume)
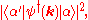
which confirms the expressions for the Green functions in the spectral representation.
The sum rule can be proved by considering the expectation value of the commutator,
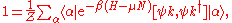
and then inserting a complete set of eigenstates into both terms of the commutator:
Swapping the labels in the first term then gives
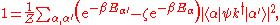
which is exactly the result of the integration of
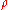.Non-interacting case
In the non-interacting case,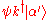 is an eigenstate with (grand-canonical) energy , where 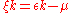is the single-particle dispersion relation measured with respect to the chemical potential. The spectral density therefore becomesFrom the commutation relations,
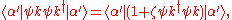
with possible factors of the volume again. The sum, which involves the thermal average of the number operator, then gives simply
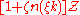, leaving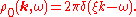The imaginary-time propagator is thus
and the retarded propagator is
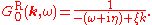
Zero-temperature limit
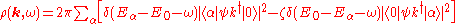
As, the spectral density becomeswhere
corresponds to the ground state. Note that only the first (second) term contributes when is positive (negative).Basic definitions
We can use `field operators' as above, or creation and annihilation operators associated with other single-particle states, perhaps eigenstates of the (noninteracting) kinetic energy. We then use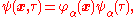where
is the annihilation operator for the single-particle state and is that state's wavefunction in the position basis. This gives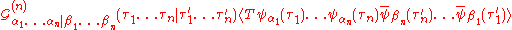with a similar expression for
.Two-point functions
These depend only on the difference of their time arguments, so that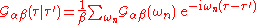and
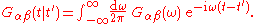
We can again define retarded and advanced functions in the obvious way; these are related to the time-ordered function in the same way as above.
The same periodicity properties as described in above apply to
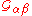. Specifically,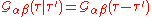and
for
.Spectral representation
In this case,where
and are many-body states.The expressions for the Green functions are modified in the obvious ways:
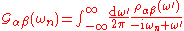
and
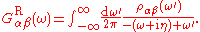
Their analyticity properties are identical. The proof follows exactly the same steps, except that the two matrix elements are no longer complex conjugates.
Noninteracting case
If the particular single-particle states that are chosen are `single-particle energy eigenstates', ie,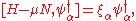then for
an eigenstate:so is
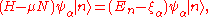
:and so is
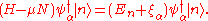
:We therefore have
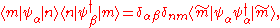
where
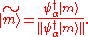
We then rewrite
and use the fact that the thermal average of the number operator gives the Bose-Einstein or Fermi-Dirac distribution function.
Finally, the spectral density simplifies to give
so that the thermal Green function is
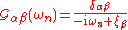
and the retarded Green function is
Note that the noninteracting Green function is diagonal, but this will not be true in the interacting case.
See also
- Fluctuation theoremFluctuation theoremThe fluctuation theorem , which originated from statistical mechanics, deals with the relative probability that the entropy of a system which is currently away from thermodynamic equilibrium will increase or decrease over a given amount of time...
- Green-Kubo relationsGreen-Kubo relationsThe Green–Kubo relations give the exact mathematical expression for transport coefficients in terms of integrals of time correlation functions.-Thermal and mechanical transport processes:...
- Linear response functionLinear response functionA linear response function describes the input-output relationship of a signal transducer such as a radio turning electromagnetic waves into music or a neuron turning synaptic input into a response...
- Lindblad equationLindblad equationIn quantum mechanics, the Kossakowski–Lindblad equation or master equation in the Lindblad form is the most general type of markovian and time-homogeneous master equation describing non-unitary evolution of the density matrix \rho that is trace preserving and completely positive for any initial...
Books
- Bonch-Bruevich V. L., Tyablikov S. V.Sergei TyablikovSergei Vladimirovich Tyablikov was a Russian theoretical physicist known for his significant contributions to statistical mechanics, solid-state physics, and for the development of the double-time Green function's formalism.-Biography:...
(1962): The Green Function Method in Statistical Mechanics. North Holland Publishing Co. - Abrikosov, A. A., Gorkov, L. P. and Dzyaloshinski, I. E. (1963): Methods of Quantum Field Theory in Statistical Physics Englewood Cliffs: Prentice-Hall.
- Negele, J. W. and Orland, H. (1988): Quantum Many-Particle Systems AddisonWesley.
- Zubarev D. N.Dmitry ZubarevDmitry Nikolaevich Zubarev was a Russian theoretical physicist known for his contributions to statistical mechanics, non-equilibrium thermodynamics, plasma physics, theory of turbulence, and to the development of the double-time Green function's formalism....
, Morozov V., Ropke G. (1996): Statistical Mechanics of Nonequilibrium Processes: Basic Concepts, Kinetic Theory (Vol. 1). John Wiley & Sons. ISBN 3-05-501708-0. - Mattuck Richard D. (1992), A Guide to Feynman Diagrams in the Many-Body Problem, Dover Publications, ISBN 0-486-67047-3.
Papers
- Bogolyubov N. N., Tyablikov S. V.Sergei TyablikovSergei Vladimirovich Tyablikov was a Russian theoretical physicist known for his significant contributions to statistical mechanics, solid-state physics, and for the development of the double-time Green function's formalism.-Biography:...
Retarded and advanced Green functions in statistical physics, Soviet Physics Doklady, Vol. 4, p. 589 (1959). - Zubarev D. N.Dmitry ZubarevDmitry Nikolaevich Zubarev was a Russian theoretical physicist known for his contributions to statistical mechanics, non-equilibrium thermodynamics, plasma physics, theory of turbulence, and to the development of the double-time Green function's formalism....
, Double-time Green functions in statistical physics, Soviet Physics Uspekhi 3(3), 320—345 (1960).