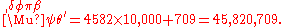Greek numerals
Encyclopedia
- The numerical signs ʹ and ͵ redirect here. For the accent, ´, see Acute accentAcute accentThe acute accent is a diacritic used in many modern written languages with alphabets based on the Latin, Cyrillic, and Greek scripts.-Apex:An early precursor of the acute accent was the apex, used in Latin inscriptions to mark long vowels.-Greek:...
.
Greek numerals are a system of representing numbers
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
using letters of the Greek alphabet
Greek alphabet
The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
. They are also known by the names Ionian numerals, Milesian numerals (from Miletus
Miletus
Miletus was an ancient Greek city on the western coast of Anatolia , near the mouth of the Maeander River in ancient Caria...
in Ionia
Ionia
Ionia is an ancient region of central coastal Anatolia in present-day Turkey, the region nearest İzmir, which was historically Smyrna. It consisted of the northernmost territories of the Ionian League of Greek settlements...
), Alexandrian numerals, or alphabetic numerals (in common with other alphabetic numerations). In modern Greece
Greece
Greece , officially the Hellenic Republic , and historically Hellas or the Republic of Greece in English, is a country in southeastern Europe....
, they are still used for ordinal number
Ordinal number (linguistics)
In linguistics, ordinal numbers are the words representing the rank of a number with respect to some order, in particular order or position . Its use may refer to size, importance, chronology, etc...
s and in situations similar to those in which Roman numerals
Roman numerals
The numeral system of ancient Rome, or Roman numerals, uses combinations of letters from the Latin alphabet to signify values. The numbers 1 to 10 can be expressed in Roman numerals as:...
are still used elsewhere in the West. For ordinary cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s numbers, however, Greece uses Arabic numerals
Arabic numerals
Arabic numerals or Hindu numerals or Hindu-Arabic numerals or Indo-Arabic numerals are the ten digits . They are descended from the Hindu-Arabic numeral system developed by Indian mathematicians, in which a sequence of digits such as "975" is read as a numeral...
.
History
Originally, before the adoption of the Greek alphabet, Linear ALinear A
Linear A is one of two scripts used in ancient Crete before Mycenaean Greek Linear B; Cretan hieroglyphs is the second script. In Minoan times, before the Mycenaean Greek dominion, Linear A was the official script for the palaces and religious activities, and hieroglyphs were mainly used on seals....
and Linear B
Linear B
Linear B is a syllabic script that was used for writing Mycenaean Greek, an early form of Greek. It pre-dated the Greek alphabet by several centuries and seems to have died out with the fall of Mycenaean civilization...
had used a different system, called Aegean numbers, with symbols for operating with the following formula: .
The earliest alphabet-related system of numerals used with the Greek letters was a set of the acrophonic Attic numerals
Attic numerals
Attic numerals were used by the ancient Greeks, possibly from the 7th century BC. They were also known as Herodianic numerals because they were first described in a 2nd century manuscript by Herodian...
, operating much like Roman numerals (which derived from this scheme), with: ; and with represented by composites of Π and a tiny version of the applicable power of ten. The acrophonic system was replaced by a new alphabetic system, sometimes called the Ionic numeral system, from the 4th century BC.
Description
Each unit (1, 2, …, 9) was assigned a separate letter, each tens (10, 20, …, 90) a separate letter, and each hundreds (100, 200, …, 900) a separate letter. This requires 27 letters, so the 24-letter Greek alphabet was extended by using three obsolete letters: digammaDigamma
Digamma is an archaic letter of the Greek alphabet which originally stood for the sound /w/ and later remained in use only as a numeral symbol for the number "6"...
ϝ for 6, qoppa
Qoppa
Koppa or Qoppa is a letter that was used in early forms of the Greek alphabet, derived from Phoenician qoph. It was originally used to denote the /k/ sound, but dropped out of use as an alphabetic character in favour of Kappa . It has remained in use as a numeral symbol in the system of Greek...
ϟ for 90, and sampi
Sampi
Sampi is an archaic letter of the Greek alphabet. It was used in addition to the classical 24 letters of the alphabet to denote some type of a sibilant sound, probably or , in some eastern Ionic dialects of ancient Greek in the 6th and 5th centuries BC...
ϡ for 900. Digamma is today most often written in its modern form ϛ, which is also called stigma
Stigma (letter)
Stigma is a ligature of the Greek letters sigma and tau , which was used in writing Greek between the middle ages and the 19th century. It is also used as a numeral symbol for the number 6...
; in Greece it is often replaced by the letter combination στ/ΣΤ. To distinguish numerals from letters they are followed in modern print by the keraia (Greek , "hornlike projection"), a symbol ( ʹ ) similar to an acute
Acute accent
The acute accent is a diacritic used in many modern written languages with alphabets based on the Latin, Cyrillic, and Greek scripts.-Apex:An early precursor of the acute accent was the apex, used in Latin inscriptions to mark long vowels.-Greek:...
sign ( ´ ) but with its own Unicode
Unicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
character (U+0374). In ancient and medieval manuscripts, number signs were written with a horizontal line above.
This alphabetic system operates on the additive principle in which the numeric values of the letters are added together to form the total. For example, 241 is represented as σμαʹ (200 + 40 + 1). A famous example is 666 (the number of the Beast
Number of the Beast
The Number of the Beast is a term in the Book of Revelation, of the New Testament, that is associated with the first Beast of Revelation chapter 13, the Beast of the sea. In most manuscripts of the New Testament and in English translations of the Bible, the number of the Beast is...
), which is represented as χξϛʹ (600 + 60 + 6) in medieval manuscripts of the Book of Revelation
Book of Revelation
The Book of Revelation is the final book of the New Testament. The title came into usage from the first word of the book in Koine Greek: apokalupsis, meaning "unveiling" or "revelation"...
.
To represent numbers from 1,000 to 999,999 the same letters are reused to serve as thousands, tens of thousands, and hundreds of thousands. A "left keraia" (Unicode U+0375, ‘Greek Lower Numeral Sign’) is put in front of thousands to distinguish them from the standard use. For example, 2011 is represented as ͵βιαʹ (2000 + 11).
| Letter | Value | Letter | Value | Letter | Value | ||
|---|---|---|---|---|---|---|---|
| αʹ | 1 | ιʹ | 10 10 (number) 10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and... |
ρʹ | 100 100 (number) 100 is the natural number following 99 and preceding 101.-In mathematics:One hundred is the square of 10... |
||
| βʹ | 2 | κʹ | 20 20 (number) 20 is the natural number following 19 and preceding 21. A group of twenty units may also be referred to as a score.-In mathematics:*20 is the basis for vigesimal number systems.... |
σʹ | 200 200 (number) 200 is the natural number following 199 and preceding 201.The number appears in the Padovan sequence, preceded by 86, 114, 151 .... |
||
| γʹ | 3 | λʹ | 30 30 (number) 30 is the natural number following 29 and preceding 31.-In mathematics:30 is the sum of the first four squares, which makes it a square pyramidal number.It is a primorial and is the smallest Giuga number.... |
τʹ | 300 300 (number) 300 is the natural number following 299 and preceding 301.- Mathematical properties :It is a triangular number and the sum of a pair of twin primes , as well as the sum of ten consecutive primes... |
||
| δʹ | 4 | μʹ | 40 40 (number) 40 is the natural number following 39 and preceding 41.Despite being related to the word "four" , 40 is spelled "forty", and not "fourty"... |
υʹ | 400 400 (number) 400 is the natural number following 399 and preceding 401. - Mathematical properties :400 is the square of 20.A circle is divided into 400 grads, which is equal to 360 degrees and 2π radians... |
||
| εʹ | 5 | νʹ | 50 50 (number) This article discusses the number fifty. For the year 50 CE, see 50. For other uses of 50, see 50 50 is the natural number following 49 and preceding 51.-In mathematics:... |
φʹ | 500 500 (number) 500 is the natural number following 499 and preceding 501.- Other fields :Five hundred is also*many NASCAR races often use the number 500 at the end of their race names 500 (five hundred) is the natural number following 499 and preceding 501.- Other fields :Five hundred is also*many NASCAR races... |
||
| or or | 6 | ξʹ | 60 60 (number) 60 is the natural number following 59 and preceding 61. Being three times twenty, 60 is called "three score" in some older literature.-In mathematics:... |
χʹ | 600 600 (number) For the year 600, see 600 BC or 600 AD.600 is the natural number following 599 and preceding 601.-Mathematical properties:Six hundred is a composite number, an abundant number, a pronic number and a Harshad number.-In other fields:... |
||
| ζʹ | 7 | οʹ | 70 70 (number) 70 is the natural number following 69 and preceding 71.-In mathematics:Its factorization makes it a sphenic number. 70 is a Pell number and a generalized heptagonal number, one of only two numbers to be both. Also, it is the seventh pentagonal number and the fourth 13-gonal number, as well as the... |
ψʹ | 700 700 (number) 700 is the natural number following 699 and preceding 701.It is the sum of four consecutive primes... |
||
| ηʹ | 8 | πʹ | 80 80 (number) 80 is the natural number following 79 and preceding 81.- In mathematics :The sum of Euler's totient function φ over the first sixteen integers is 80.... |
ωʹ | 800 800 (number) 800 is the natural number following 799 and preceding 801.It is the sum of four consecutive primes... |
||
| θʹ | 9 | ϟʹ | 90 90 (number) 90 is the natural number preceded by 89 and followed by 91.- In mathematics :*Because 90 is the sum of its unitary divisors , it is a unitary perfect number, and because it is equal to the sum of a subset of its divisors, it is a semiperfect number. 90 is a pronic number. But it is also a... |
ϡʹ | 900 900 (number) For the year 900, see 900 BC or 900 AD.900 is the natural number following 899 and preceding 901. It is the square of 30 and the sum of Euler's totient function for the first 54 integers... |
In modern Greek
Modern Greek
Modern Greek refers to the varieties of the Greek language spoken in the modern era. The beginning of the "modern" period of the language is often symbolically assigned to the fall of the Byzantine Empire in 1453, even though that date marks no clear linguistic boundary and many characteristic...
, uppercase letters are preferred, as in Φίλιππος Βʹ = Philip II
Philip II of Macedon
Philip II of Macedon "friend" + ἵππος "horse" — transliterated ; 382 – 336 BC), was a king of Macedon from 359 BC until his assassination in 336 BC. He was the father of Alexander the Great and Philip III.-Biography:...
.
Higher numbers
To represent greater numbers, the Greeks also used the myriadMyriad
Myriad , "numberlesscountless, infinite", is a classical Greek word for the number 10,000. In modern English, the word refers to an unspecified large quantity.-History and usage:...
from the old Attic numeral system in their notation. Its value is 10,000; the number of myriads was written above its symbol (Mʹ). For example (keraias replaced for technical reasons):
Other forms are also possible. When that didn't suffice the myriad myriad (one hundred million, symbol: ΜΜʹ) was used.
In his text The Sand Reckoner
The Sand Reckoner
The Sand Reckoner is a work by Archimedes in which he set out to determine an upper bound for the number of grains of sand that fit into the universe. In order to do this, he had to estimate the size of the universe according to the then-current model, and invent a way to talk about extremely...
the natural philosopher Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
gives an upper bound of the number of grains of sand required to fill the entire universe, using a contemporary estimation of its size. This would defy the then-held notion that it is impossible to name a number greater than that of the sand on a beach, or on the entire world. In order to do that, he had to devise a new numeral scheme with much greater range.
Hellenistic zero
HellenisticHellenistic civilization
Hellenistic civilization represents the zenith of Greek influence in the ancient world from 323 BCE to about 146 BCE...
astronomer
Astronomer
An astronomer is a scientist who studies celestial bodies such as planets, stars and galaxies.Historically, astronomy was more concerned with the classification and description of phenomena in the sky, while astrophysics attempted to explain these phenomena and the differences between them using...
s extended alphabetic Greek numerals into a sexagesimal positional
Positional notation
Positional notation or place-value notation is a method of representing or encoding numbers. Positional notation is distinguished from other notations for its use of the same symbol for the different orders of magnitude...
numbering system
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
by limiting each position to a maximum value of 50 + 9 and including a special symbol for zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
, which was also used alone like our modern zero, more than as a simple placeholder. However, the positions were usually limited to the fractional part of a number (called minute
Minute
A minute is a unit of measurement of time or of angle. The minute is a unit of time equal to 1/60th of an hour or 60 seconds. In the UTC time scale, a minute on rare occasions has 59 or 61 seconds; see leap second. The minute is not an SI unit; however, it is accepted for use with SI units...
s, seconds, thirds, fourths, etc.) — they were not used for the integral
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
part of a number. This system was probably adapted from Babylonian numerals
Babylonian numerals
Babylonian numerals were written in cuneiform, using a wedge-tipped reed stylus to make a mark on a soft clay tablet which would be exposed in the sun to harden to create a permanent record....
by Hipparchus
Hipparchus
Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
c. 140 BC. It was then used by Ptolemy
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
(c. 140), Theon
Theon of Alexandria
Theon was a Greek scholar and mathematician who lived in Alexandria, Egypt. He edited and arranged Euclid's Elements and Ptolemy's Handy Tables, as well as writing various commentaries...
(c. 380), and Theon's daughter Hypatia
Hypatia of Alexandria
Hypatia was an Egyptian Neoplatonist philosopher who was the first notable woman in mathematics. As head of the Platonist school at Alexandria, she also taught philosophy and astronomy...
(died 415).
In Ptolemy's table of chords
Ptolemy's table of chords
The table of chords, created by the astronomer and geometer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function...
, the first fairly extensive trigonometric table, there were 360 rows, portions of which looked as follows:
-
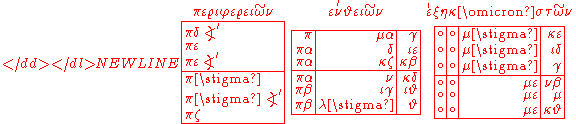
Each number in the first column, labeled περιφεριῶν, is the number of degrees of arc on a circle. Each number in the second column, labeled ενθειῶν, is the length of the corresponding chord of the circle, when the diameter is 120. Thus πδ represents an 84° arc, and the ∠' after it means one-half, so that πδ∠' means 84.5°. In the next column we see π μα γ, meaning 80 + 41/60 + 3/602. That is the length of the chord corresponding to an arc of 84.5° when the diameter of the circle is 120. The next column, labeled ὲξηκοστῶν, for "sixtieths", is the number to be added to the chord length for each 1° increase in the arc, over the span of the next 12°. Thus that last column was used for linear interpolationLinear interpolationLinear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
.
The Greek sexagesimal place holder or zero symbol changed over time. The symbol used on papyriPapyrusPapyrus is a thick paper-like material produced from the pith of the papyrus plant, Cyperus papyrus, a wetland sedge that was once abundant in the Nile Delta of Egypt....
during the second century was a very small circle with an overbar several diameters long, terminated or not at both ends in various ways. Later, the overbar shortened to only one diameter, similar to our modern o macron (ō) which was still being used in late medieval Arabic manuscripts whenever alphabetic numerals were used. But the overbar was omitted in ByzantineByzantine EmpireThe Byzantine Empire was the Eastern Roman Empire during the periods of Late Antiquity and the Middle Ages, centred on the capital of Constantinople. Known simply as the Roman Empire or Romania to its inhabitants and neighbours, the Empire was the direct continuation of the Ancient Roman State...
manuscripts, leaving a bare ο (omicron). This gradual change from an invented symbol to ο does not support the hypothesis that the latter was the initial of ουδέν meaning "nothing".
Some of Ptolemy's true zeros appeared in the first line of each of his eclipse tables, where they were a measure of the angular separation between the center of the MoonMoonThe Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
and either the center of the SunSunThe Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
(for solar eclipseSolar eclipseAs seen from the Earth, a solar eclipse occurs when the Moon passes between the Sun and the Earth, and the Moon fully or partially blocks the Sun as viewed from a location on Earth. This can happen only during a new moon, when the Sun and the Moon are in conjunction as seen from Earth. At least...
s) or the center of EarthEarthEarth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
's shadow (for lunar eclipseLunar eclipseA lunar eclipse occurs when the Moon passes behind the Earth so that the Earth blocks the Sun's rays from striking the Moon. This can occur only when the Sun, Earth, and Moon are aligned exactly, or very closely so, with the Earth in the middle. Hence, a lunar eclipse can only occur the night of a...
s). All of these zeros took the form 0 | 0 0, where Ptolemy actually used three of the symbols described in the previous paragraph. The vertical bar (|) indicates that the integral part on the left was in a separate column labeled in the headings of his tables as digits (of five arc-minutes each), whereas the fractional part was in the next column labeled minute of immersion, meaning sixtieths (and thirty-six-hundredths) of a digit.
See also
- Attic numeralsAttic numeralsAttic numerals were used by the ancient Greeks, possibly from the 7th century BC. They were also known as Herodianic numerals because they were first described in a 2nd century manuscript by Herodian...
- GematriaGematriaGematria or gimatria is a system of assigning numerical value to a word or phrase, in the belief that words or phrases with identical numerical values bear some relation to each other, or bear some relation to the number itself as it may apply to a person's age, the calendar year, or the like...
- Greek numerals in Unicode (acrophonic, not alphabetic, numerals)
- IsopsephyIsopsephyIsopsephy is the Greek word for the practice of adding up the number values of the letters in a word to form a single number. The early Greeks used pebbles arranged in patterns to learn arithmetic and geometry....
External links
- Attic numerals