In classical mechanics

Classical mechanics

In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...

, the gravitational potential at a location is equal to the work (energy

Energy

In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...

 transferred) per unit mass that is done by the force of gravity as an object moves to that location from a reference location. It is analogous to the electric potential

Electric potential

In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...

 with mass

Mass

Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...

 playing the role of charge

Charge (physics)

In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...

. By convention, the gravitational potential is defined as zero infinitely far away from any mass. As a result it is negative elsewhere.

In mathematics the gravitational potential is also known as the Newtonian potential

Newtonian potential

In mathematics, the Newtonian potential or Newton potential is an operator in vector calculus that acts as the inverse to the negative Laplacian, on functions that are smooth and decay rapidly enough at infinity. As such, it is a fundamental object of study in potential theory...

 and is fundamental in the study of potential theory

Potential theory

In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...

.

Potential energy

The gravitational potential (V) is the potential energy

Potential energy

In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...

 (U) per unit mass:


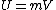
where m is the mass of the object. The potential energy is the negative of the work done by the gravitational field moving the body to its given position in space from infinity. If the body has a mass of 1 unit, then the potential energy to be assigned to that body is equal to the gravitational potential. So the potential can be interpreted as the negative of the work done by the gravitational field moving a unit mass in from infinity.

In some situations, the equations can be simplified by assuming a field that is nearly independent of position. For instance, in daily life, in the region close to the surface of the Earth, the gravitational acceleration can be considered constant. In that case, the difference in potential energy from one height to another is to a good approximation linearly related to the difference in height:

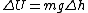
Mathematical form

The potential

Potential

*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...

 V at a distance x from a point mass

Point particle

A point particle is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension: being zero-dimensional, it does not take up space...

 of mass M is
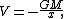
where G is the gravitational constant

Gravitational constant

The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...

. The potential has units of energy per unit mass, e.g., J/kg in the MKS

Mks system of units

The MKS system of units is a physical system of units that expresses any given measurement using fundamental units of the metre, kilogram, and/or second ....

 system. By convention, it is always negative where it is defined, and as x tends to infinity, it approaches zero.

The gravitational field

Gravitational field

The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...

, and thus the acceleration of a small body in the space around the massive object, is the negative gradient

Gradient

In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....

 of the gravitational potential. Because the potential has no angular components, its gradient is:
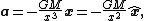
where x is a vector of length x pointing from the point mass toward the small body and 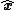is a unit vector pointing from the point mass toward the small body. The magnitude of the acceleration therefore follows an inverse square law: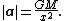

The potential associated with a mass distribution

Mass distribution

Mass distribution is a term used in physics and mechanics and describes the spatial distribution of mass within a solid body. In principle, it is relevant also for gases or liquids, but on earth their mass distribution is almost homogeneous.-Astronomy:...

 is the superposition of the potentials of point masses. If the mass distribution is a finite collection of point masses, and if the point masses are located at the points x₁, ..., x_n and have masses m₁, ..., m_n, then the potential of the distribution at the point x is:
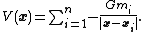
If the mass distribution is given as a mass measure dm on three-dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

 R³, then the potential is the convolution

Convolution

In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...

 of −G/|r| with dm. In good cases this equals the integral
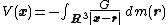
where |x − r| is the distance

Euclidean distance

In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...

 between the points x and r. If there is a function ρ(r) representing the density of the distribution at r, so that dm(r) = ρ(r)dv(r), where dv(r) is the Euclidean volume element

Volume element

In mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates...

, then the gravitational potential is the volume integral

Volume integral

In mathematics — in particular, in multivariable calculus — a volume integral refers to an integral over a 3-dimensional domain....

If V is a potential function coming from a continuous mass distribution ρ(r), then ρ can be recovered using the Laplace operator

Laplace operator

In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...

 Δ using the formula:
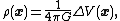
This holds pointwise whenever ρ is continuous and is zero outside of a bounded set. In general, the mass measure dm can be recovered in the same way if the Laplace operator is taken in the sense of distribution

Distribution (mathematics)

In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...

s. As a consequence, the gravitational potential satisfies Poisson's equation

Poisson's equation

In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...

. See also Green's function for the three-variable Laplace equation

Green's function for the three-variable Laplace equation

In physics, the Green's function for Laplace's equation in three variables is used to describe the response of a particular type of physical system to a point source...

 and Newtonian potential

Newtonian potential

In mathematics, the Newtonian potential or Newton potential is an operator in vector calculus that acts as the inverse to the negative Laplacian, on functions that are smooth and decay rapidly enough at infinity. As such, it is a fundamental object of study in potential theory...

.

Spherical symmetry

A spherically symmetric mass distribution behaves to an observer completely outside the distribution as though all of the mass were concentrated at the center, and thus effectively as a point mass, by the shell theorem

Shell theorem

In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body...

. On the surface of the earth, the acceleration is given by so-called standard gravity

Standard gravity

Standard gravity, or standard acceleration due to free fall, usually denoted by g0 or gn, is the nominal acceleration of an object in a vacuum near the surface of the Earth. It is defined as precisely , or about...

 g, approximately 9.8 m/s², although this value varies slightly with latitude and altitude: The magnitude of the acceleration is a little larger at the poles than at the equator because Earth is an oblate spheroid.

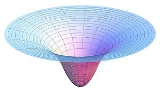
Within a spherically symmetric mass distribution, it is possible to solve Poisson's equation in spherical coordinates. Within a uniform spherical body of radius R and density σ, the gravitational force g inside the sphere varies linearly with distance r from the center, giving the gravitational potential inside the sphere, which is


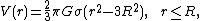
which differentiably connects to the potential function for the outside of the sphere (see the figure at the top).

General relativity

In general relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

, the gravitational potential is replaced by the metric tensor

Metric tensor (general relativity)

In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...

.

Multipole expansion

The potential at a point x is given by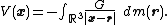

The potential can be expanded in a series of Legendre polynomials. Represent the points x and r as position vectors relative to the center of mass. The denominator in the integral is expressed as the square root of the square to give

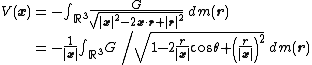
where in the last integral, r = |r| and θ is the angle between x and r.

The integrand can be expanded as a Taylor series

Taylor series

In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....

 in Z = r/|x|, by explicit calculation of the coefficients. A less laborious way of achieving the same result is by using the generalized binomial theorem

Binomial theorem

In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...

. The resulting series is the generating function

Generating function

In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...

 for the Legendre polynomials:


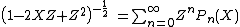
valid for |X| ≤ 1 and |Z| < 1. The coefficients P_n are the Legendre polynomials of degree n. Therefore, the Taylor coefficients of the integrand are given by the Legendre polynomials in X = cos θ. So the potential can be expanded in a series that is convergent for positions x such that r < |x| for all mass elements of the system (i.e., outside a sphere, centered at the center of mass, that encloses the system):
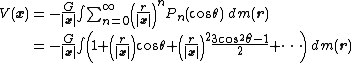
The integral is the component of the center of mass in the x direction; this vanishes because the vector x emanates from the center of mass. So, bringing the integral under the sign of the summation gives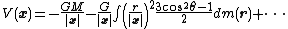

This shows that elongation of the body causes a lower potential in the direction of elongation, and a higher potential in perpendicular directions, compared to the potential due to a spherical mass, if we compare cases with the same distance to the center of mass. (If we compare cases with the same distance to the surface the opposite is true.)

Numerical values

The absolute value of gravitational potential with respect to the Earth

Earth

Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...

, the Sun

Sun

The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...

, and the Milky Way

Milky Way

The Milky Way is the galaxy that contains the Solar System. This name derives from its appearance as a dim un-resolved "milky" glowing band arching across the night sky...

 is given in the following table. It is half the square of the escape velocity

Escape velocity

In physics, escape velocity is the speed at which the kinetic energy plus the gravitational potential energy of an object is zero gravitational potential energy is negative since gravity is an attractive force and the potential is defined to be zero at infinity...

.

Location	W.r.t. Earth Earth Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...	W.r.t. Sun Sun The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...	W.r.t. Milky Way Milky Way The Milky Way is the galaxy that contains the Solar System. This name derives from its appearance as a dim un-resolved "milky" glowing band arching across the night sky...
Earth's surface	60 MJ/kg	900 MJ/kg	≥ 130 GJ/kg
LEO Low Earth orbit A low Earth orbit is generally defined as an orbit within the locus extending from the Earth’s surface up to an altitude of 2,000 km...	57 MJ/kg	900 MJ/kg	≥ 130 GJ/kg
Voyager 1 Voyager 1 The Voyager 1 spacecraft is a 722-kilogram space probe launched by NASA in 1977, to study the outer Solar System and eventually interstellar space. Operating for as of today , the spacecraft receives routine commands and transmits data back to the Deep Space Network. At a distance of as of...  (17,000 million km from Earth)	23 J/kg	8 MJ/kg	≥ 130 GJ/kg
0.1 light-year Light-year A light-year, also light year or lightyear is a unit of length, equal to just under 10 trillion kilometres...  from Earth	0.4 J/kg	140 kJ/kg	≥ 130 GJ/kg

Compare the gravity at these locations.

See also

• Applications of Legendre polynomials in physics