
Glossary of ring theory
Encyclopedia
Ring theory
is the branch of mathematics
in which rings
are studied: that is, structures supporting both an addition
and a multiplication
operation. This is a glossary of some terms of the subject.
: A ring is a set R with two binary operation
s, usually called addition (+) and multiplication (*), such that R is an abelian group
under addition, a monoid
under multiplication, and such that multiplication is both left and right distributive over addition. Note that rings are assumed to have multiplicative identities unless otherwise noted. The additive identity is denoted by 0 and the multiplicative identity by 1.
Subring
: A subset S of the ring (R,+,*) which remains a ring when + and * are restricted to S and contains the multiplicative identity 1 of R is called a subring of R.
of R, known as the center of R.
Divisor
: In an integral domain R, an element a is called a divisor of the element b (and we say a divides b) if there exists an element x in R with ax = b.
Idempotent : An element r of a ring is idempotent if r2 = r.
Unit
or invertible element : An element r of the ring R is a unit if there exists an element r−1 such that rr−1=r−1r=1. This element r−1 is uniquely determined by r and is called the multiplicative inverse of r. The set of units forms a group
under multiplication.
Irreducible
: An element x of an integral domain is irreducible if it is not a unit and for any elements a and b such that x=ab, either a or b is a unit. Note that every prime element is irreducible, but not necessarily vice versa.
Prime element
: An element x of an integral domain is a prime element if it is not zero and not a unit and whenever x divides a product ab, x divides a or x divides b.
Nilpotent
: An element r of R is nilpotent if there exists a positive integer n such that rn = 0.
Zero divisor
: A nonzero element r of R is a zero divisor if there exists a nonzero element s in R such that sr=0 or rs=0.
s {a+I : a∈R} together with the operations (a+I)+(b+I)=(a+b)+I and (a+I)(b+I)=ab+I. The relationship between ideals, homomorphisms, and factor rings is summed up in the fundamental theorem on homomorphisms
.
Finitely generated ideal : A left ideal I is finitely generated if there exist finitely many elements a1,...,an such that I = Ra1 + ... + Ran. A right ideal I is finitely generated if there exist finitely many elements a1,...,an such that I = a1R + ... + anR. A two-sided ideal I is finitely generated if there exist finitely many elements a1,...,an such that I = Ra1R + ... + RanR.
Ideal
: A left ideal I of R is a subgroup of R such that aI ⊆ I for all a∈R. A right ideal is a subgroup of R such that Ia⊆I for all a∈R. An ideal (sometimes called a two-sided ideal for emphasis) is a subgroup which is both a left ideal and a right ideal.
Jacobson radical
: The intersection of all maximal left ideals in a ring forms a two-sided ideal, the Jacobson radical of the ring.
Kernel
of a ring homomorphism : The kernel of a ring homomorphism f : R → S is the set of all elements x of R such that f(x) = 0. Every ideal is the kernel of a ring homomorphism and vice versa.
Maximal ideal
: A left ideal M of the ring R is a maximal left ideal if M ≠ R and the only left ideals containing M are R and M itself. Maximal right ideals are defined similarly. In commutative rings, there is no difference, and one speaks simply of maximal ideals.
Nil ideal
: An ideal is nil if it consists only of nilpotent elements.
Nilpotent ideal
: An ideal I is nilpotent if its powers Ik are {0} for k large enough. Every nilpotent ideal is nil, but the converse is not true in general.
Nilradical : The set of all nilpotent elements in a commutative ring forms an ideal, the nilradical of the ring. The nilradical is equal to the intersection of all the ring's prime ideal
s. It is contained in, but in general not equal to, the ring's Jacobson Radical.
Prime ideal
: An ideal P in a commutative ring
R is prime if P ≠ R and if for all a and b in R with ab in P, we have a in P or b in P. Every maximal ideal in a commutative ring is prime. There is also a definition of prime ideal for noncommutative rings.
Principal ideal
: A principal left ideal in a ring R is a left ideal of the form Ra for some element a of R. A principal right ideal is a right ideal of the form aR for some element a of R. A principal ideal is a two-sided ideal of the form RaR for some element a of R.
Radical of an ideal
: The radical of an ideal I in a commutative ring
consists of all those ring elements a power of which lies in I. It is equal to the intersection of all prime ideals containing I.
Ring homomorphism
: A function
f : R → S between rings (R,+,*) and (S,⊕,×) is a ring homomorphism if it satisfies
Ring monomorphism : A ring homomorphism that is injective is a ring monomorphism.
Ring isomorphism : A ring homomorphism that is bijective is a ring isomorphism. The inverse of a ring isomorphism is also a ring isomorphism. Two rings are isomorphic if there exists a ring isomorphism between them. Isomorphic rings can be thought as essentially the same, only with different labels on the individual elements.
: A ring satisfying the descending chain condition for left ideals is left artinian; if it satisfies the descending chain condition for right ideals, it is right artinian; if it is both left and right artinian, it is called artinian. Artinian rings are noetherian.
Boolean ring
: A ring in which every element is idempotent is a boolean ring.
Commutative ring
: A ring R is commutative if the multiplication is commutative, i.e. rs=sr for all r,s∈R.
Dedekind domain
: A Dedekind domain is an integral domain in which every ideal has a unique factorization into prime ideals.
Division ring
or skew field : A ring in which every nonzero element is a unit and 1≠0 is a division ring.
Domain (ring theory)
: A domain is a ring without zero divisors and in which 1≠0. This is the noncommutative generalization of integral domain.
Euclidean domain
: A Euclidean domain is an integral domain in which a degree function is defined so that "division with remainder" can be carried out. It is so named because the Euclidean algorithm
is a well-defined algorithm in these rings. All Euclidean domains are principal ideal domains.
Field
: A field is a commutative division ring. Every finite division ring is a field, as is every finite integral domain. Field theory
is in fact an older branch of mathematics than ring theory.
Finitely presented algebra: If R is a commutative ring
and A is an R-algebra, then A is a finitely presented R-algebra if it is a quotient
of a polynomial ring
over R in finitely many variables by a finitely generated ideal.
Integral domain or entire ring : A commutative ring
without zero divisor
s and in which 1≠0 is an integral domain.
Invariant basis number
: A ring R has invariant basis number if Rm isomorphic to Rn as R-modules
implies m=n.
Local ring
: A ring with a unique maximal left ideal is a local ring. These rings also have a unique maximal right ideal, and the left and the right unique maximal ideals coincide. Any ring can be made local via localization
.
Noetherian ring
: A ring satisfying the ascending chain condition
for left ideals is left noetherian; a ring satisfying the ascending chain condition for right ideals is right noetherian; a ring that is both left and right noetherian is noetherian. A ring is left noetherian if and only if all its left ideals are finitely generated; analogously for right noetherian rings.
Prime ring
: A non-trivial ring R is called a prime ring if for any two elements a and b of R with aRb = 0, we have either a = 0 or b = 0. This is equivalent to saying that the zero ideal is a prime ideal. Every simple ring
and every domain
is a prime ring.
Primitive ring
: A left primitive ring is a ring that has a faithful simple
left R-module
. Every simple ring
is primitive. Primitive rings are prime
.
Principal ideal domain
: An integral domain in which every ideal is principal is a principal ideal domain. All principal ideal domains are unique factorization domains.
Semisimple ring : A semisimple ring is a ring R that has a "nice" decomposition, in the sense that R is a semisimple
left R-module. Every semisimple ring is also Noetherian, and has no nilpotent ideals. Any ring can be made semi-simple if it is divided by its Jacobson radical
.
Simple ring
: A non-zero ring with no non-zero two-sided ideals is a simple ring.
Trivial ring or zero ring: The ring consisting only of a single element 0=1. Zero ring also has another meaning, see below.
Unique factorization domain
or factorial ring: An integral domain R in which every non-zero non-unit
element can be written as a product of prime element
s of R. This essentially means that every non-zero non-unit can be written uniquely as a product of irreducible elements.
Zero ring
or null ring: A rng
(ring without 1) in which the product of any two elements is 0 (the additive neutral element). Also, the zero ring, the ring consisting only of a single element 0=1 (see trivial ring, above).
of a family of rings : This is a way to construct a new ring from given rings by taking the cartesian product
of the given rings and defining the algebraic operations component-wise.
Endomorphism ring
: A ring formed by the endomorphism
s of an algebraic structure. Usually its multiplication is taken to be function composition
, while its addition is pointwise addition of the images.
Localization of a ring
: A technique to turn a given set of elements of a ring into units. It is named Localization because it can be used to make any given ring into a local ring. To localize a ring R, take a multiplicatively closed subset S containing no zero divisor
s, and formally define their multiplicative inverses, which shall be added into R.
Opposite ring
Formal power series
ring
Laurent polynomial ring
Monoid ring
Polynomial ring
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
is the branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
in which rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
are studied: that is, structures supporting both an addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and a multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
operation. This is a glossary of some terms of the subject.
Definition of a ring
RingRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
: A ring is a set R with two binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s, usually called addition (+) and multiplication (*), such that R is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under addition, a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under multiplication, and such that multiplication is both left and right distributive over addition. Note that rings are assumed to have multiplicative identities unless otherwise noted. The additive identity is denoted by 0 and the multiplicative identity by 1.
Subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
: A subset S of the ring (R,+,*) which remains a ring when + and * are restricted to S and contains the multiplicative identity 1 of R is called a subring of R.
Types of elements
Central : An element r of a ring R is central if xr = rx for all x in R. The set of all central elements forms a subringSubring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of R, known as the center of R.
Divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
: In an integral domain R, an element a is called a divisor of the element b (and we say a divides b) if there exists an element x in R with ax = b.
Idempotent : An element r of a ring is idempotent if r2 = r.
Unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
or invertible element : An element r of the ring R is a unit if there exists an element r−1 such that rr−1=r−1r=1. This element r−1 is uniquely determined by r and is called the multiplicative inverse of r. The set of units forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under multiplication.
Irreducible
Irreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
: An element x of an integral domain is irreducible if it is not a unit and for any elements a and b such that x=ab, either a or b is a unit. Note that every prime element is irreducible, but not necessarily vice versa.
Prime element
Prime element
In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...
: An element x of an integral domain is a prime element if it is not zero and not a unit and whenever x divides a product ab, x divides a or x divides b.
Nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
: An element r of R is nilpotent if there exists a positive integer n such that rn = 0.
Zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
: A nonzero element r of R is a zero divisor if there exists a nonzero element s in R such that sr=0 or rs=0.
Homomorphisms and ideals
Factor ring or quotient ring : Given a ring R and an ideal I of R, the factor ring is the ring formed by the set R/I of cosetCoset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s {a+I : a∈R} together with the operations (a+I)+(b+I)=(a+b)+I and (a+I)(b+I)=ab+I. The relationship between ideals, homomorphisms, and factor rings is summed up in the fundamental theorem on homomorphisms
Fundamental theorem on homomorphisms
In abstract algebra, the fundamental theorem on homomorphisms, also known as the fundamental homomorphism theorem, relates the structure of two objects between which a homomorphism is given, and of the kernel and image of the homomorphism....
.
Finitely generated ideal : A left ideal I is finitely generated if there exist finitely many elements a1,...,an such that I = Ra1 + ... + Ran. A right ideal I is finitely generated if there exist finitely many elements a1,...,an such that I = a1R + ... + anR. A two-sided ideal I is finitely generated if there exist finitely many elements a1,...,an such that I = Ra1R + ... + RanR.
Ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
: A left ideal I of R is a subgroup of R such that aI ⊆ I for all a∈R. A right ideal is a subgroup of R such that Ia⊆I for all a∈R. An ideal (sometimes called a two-sided ideal for emphasis) is a subgroup which is both a left ideal and a right ideal.
Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
: The intersection of all maximal left ideals in a ring forms a two-sided ideal, the Jacobson radical of the ring.
Kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of a ring homomorphism : The kernel of a ring homomorphism f : R → S is the set of all elements x of R such that f(x) = 0. Every ideal is the kernel of a ring homomorphism and vice versa.
Maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
: A left ideal M of the ring R is a maximal left ideal if M ≠ R and the only left ideals containing M are R and M itself. Maximal right ideals are defined similarly. In commutative rings, there is no difference, and one speaks simply of maximal ideals.
Nil ideal
Nil ideal
In mathematics, more specifically ring theory, an ideal of a ring is said to be a nil ideal if each of its elements is nilpotent. The nilradical of a commutative ring is an example of a nil ideal; in fact, it is the ideal of the ring maximal with respect to the property of being nil...
: An ideal is nil if it consists only of nilpotent elements.
Nilpotent ideal
Nilpotent ideal
In mathematics, more specifically ring theory, an ideal, I, of a ring is said to be a nilpotent ideal, if there exists a natural number k such that Ik = 0. By Ik, it is meant the additive subgroup generated by the set of all products of k elements in I...
: An ideal I is nilpotent if its powers Ik are {0} for k large enough. Every nilpotent ideal is nil, but the converse is not true in general.
Nilradical : The set of all nilpotent elements in a commutative ring forms an ideal, the nilradical of the ring. The nilradical is equal to the intersection of all the ring's prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s. It is contained in, but in general not equal to, the ring's Jacobson Radical.
Prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
: An ideal P in a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R is prime if P ≠ R and if for all a and b in R with ab in P, we have a in P or b in P. Every maximal ideal in a commutative ring is prime. There is also a definition of prime ideal for noncommutative rings.
Principal ideal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
: A principal left ideal in a ring R is a left ideal of the form Ra for some element a of R. A principal right ideal is a right ideal of the form aR for some element a of R. A principal ideal is a two-sided ideal of the form RaR for some element a of R.
Radical of an ideal
Radical of an ideal
In commutative ring theory, a branch of mathematics, the radical of an ideal I is an ideal such that an element x is in the radical if some power of x is in I. A radical ideal is an ideal that is its own radical...
: The radical of an ideal I in a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
consists of all those ring elements a power of which lies in I. It is equal to the intersection of all prime ideals containing I.
Ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
: A function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f : R → S between rings (R,+,*) and (S,⊕,×) is a ring homomorphism if it satisfies
-
- f(a + b) = f(a) ⊕ f(b)
- f(a * b) = f(a) × f(b)
- f(1) = 1
- for all elements a and b of R.
Ring monomorphism : A ring homomorphism that is injective is a ring monomorphism.
Ring isomorphism : A ring homomorphism that is bijective is a ring isomorphism. The inverse of a ring isomorphism is also a ring isomorphism. Two rings are isomorphic if there exists a ring isomorphism between them. Isomorphic rings can be thought as essentially the same, only with different labels on the individual elements.
Types of rings
Artinian ringArtinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
: A ring satisfying the descending chain condition for left ideals is left artinian; if it satisfies the descending chain condition for right ideals, it is right artinian; if it is both left and right artinian, it is called artinian. Artinian rings are noetherian.
Boolean ring
Boolean ring
In mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
: A ring in which every element is idempotent is a boolean ring.
Commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
: A ring R is commutative if the multiplication is commutative, i.e. rs=sr for all r,s∈R.
Dedekind domain
Dedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
: A Dedekind domain is an integral domain in which every ideal has a unique factorization into prime ideals.
Division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
or skew field : A ring in which every nonzero element is a unit and 1≠0 is a division ring.
Domain (ring theory)
Domain (ring theory)
In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
: A domain is a ring without zero divisors and in which 1≠0. This is the noncommutative generalization of integral domain.
Euclidean domain
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
: A Euclidean domain is an integral domain in which a degree function is defined so that "division with remainder" can be carried out. It is so named because the Euclidean algorithm
Euclidean algorithm
In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
is a well-defined algorithm in these rings. All Euclidean domains are principal ideal domains.
Field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
: A field is a commutative division ring. Every finite division ring is a field, as is every finite integral domain. Field theory
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
is in fact an older branch of mathematics than ring theory.
Finitely presented algebra: If R is a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
and A is an R-algebra, then A is a finitely presented R-algebra if it is a quotient
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
of a polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
over R in finitely many variables by a finitely generated ideal.
Integral domain or entire ring : A commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
without zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s and in which 1≠0 is an integral domain.
Invariant basis number
Invariant basis number
In mathematics, the invariant basis number property of a ring R is the property that all free modules over R are similarly well-behaved as vector spaces, with respect to the uniqueness of their ranks.-Definition:...
: A ring R has invariant basis number if Rm isomorphic to Rn as R-modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
implies m=n.
Local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
: A ring with a unique maximal left ideal is a local ring. These rings also have a unique maximal right ideal, and the left and the right unique maximal ideals coincide. Any ring can be made local via localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
.
Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
: A ring satisfying the ascending chain condition
Ascending chain condition
The ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...
for left ideals is left noetherian; a ring satisfying the ascending chain condition for right ideals is right noetherian; a ring that is both left and right noetherian is noetherian. A ring is left noetherian if and only if all its left ideals are finitely generated; analogously for right noetherian rings.
Prime ring
Prime ring
In abstract algebra, a non-trivial ring R is a prime ring if for any two elements a and b of R, arb = 0 for all r in R implies that either a = 0 or b = 0. Prime ring can also refer to the subring of a field determined by its characteristic...
: A non-trivial ring R is called a prime ring if for any two elements a and b of R with aRb = 0, we have either a = 0 or b = 0. This is equivalent to saying that the zero ideal is a prime ideal. Every simple ring
Simple ring
In abstract algebra, a simple ring is a non-zero ring that has no ideal besides the zero ideal and itself. A simple ring can always be considered as a simple algebra. This notion must not be confused with the related one of a ring being simple as a left module over itself...
and every domain
Domain (ring theory)
In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
is a prime ring.
Primitive ring
Primitive ring
In the branch of abstract algebra known as ring theory, a left primitive ring is a ring which has a faithful simple left module. Well known examples include endomorphism rings of vector spaces and Weyl algebras over fields of characteristic zero.- Definition :...
: A left primitive ring is a ring that has a faithful simple
Simple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
left R-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. Every simple ring
Simple ring
In abstract algebra, a simple ring is a non-zero ring that has no ideal besides the zero ideal and itself. A simple ring can always be considered as a simple algebra. This notion must not be confused with the related one of a ring being simple as a left module over itself...
is primitive. Primitive rings are prime
Prime ring
In abstract algebra, a non-trivial ring R is a prime ring if for any two elements a and b of R, arb = 0 for all r in R implies that either a = 0 or b = 0. Prime ring can also refer to the subring of a field determined by its characteristic...
.
Principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
: An integral domain in which every ideal is principal is a principal ideal domain. All principal ideal domains are unique factorization domains.
Semisimple ring : A semisimple ring is a ring R that has a "nice" decomposition, in the sense that R is a semisimple
Semisimple module
In mathematics, especially in the area of abstract algebra known as module theory, a semisimple module or completely reducible module is a type of module that can be understood easily from its parts. A ring which is a semisimple module over itself is known as an artinian semisimple ring...
left R-module. Every semisimple ring is also Noetherian, and has no nilpotent ideals. Any ring can be made semi-simple if it is divided by its Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
.
Simple ring
Simple ring
In abstract algebra, a simple ring is a non-zero ring that has no ideal besides the zero ideal and itself. A simple ring can always be considered as a simple algebra. This notion must not be confused with the related one of a ring being simple as a left module over itself...
: A non-zero ring with no non-zero two-sided ideals is a simple ring.
Trivial ring or zero ring: The ring consisting only of a single element 0=1. Zero ring also has another meaning, see below.
Unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
or factorial ring: An integral domain R in which every non-zero non-unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
element can be written as a product of prime element
Prime element
In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...
s of R. This essentially means that every non-zero non-unit can be written uniquely as a product of irreducible elements.
Zero ring
Zero ring
In ring theory, a branch of mathematics, a zero ring is a ring in which the product of any two elements is 0 . In ring theory, a branch of mathematics, a zero ring is a ring (without unity) in which the product of any two elements is 0 (the additive identity element). In ring theory, a branch of...
or null ring: A rng
Rng (algebra)
In abstract algebra, a rng is an algebraic structure satisfying the same properties as a ring, except that multiplication need not have an identity element...
(ring without 1) in which the product of any two elements is 0 (the additive neutral element). Also, the zero ring, the ring consisting only of a single element 0=1 (see trivial ring, above).
Ring constructions
Direct productDirect product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
of a family of rings : This is a way to construct a new ring from given rings by taking the cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of the given rings and defining the algebraic operations component-wise.
Endomorphism ring
Endomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
: A ring formed by the endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s of an algebraic structure. Usually its multiplication is taken to be function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, while its addition is pointwise addition of the images.
Localization of a ring
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
: A technique to turn a given set of elements of a ring into units. It is named Localization because it can be used to make any given ring into a local ring. To localize a ring R, take a multiplicatively closed subset S containing no zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s, and formally define their multiplicative inverses, which shall be added into R.
Opposite ring
Opposite ring
In algebra, the opposite of a ring is another ring with the same elements and addition operation, but with the multiplication performed in the reverse order....
- Given a ring R, its opposite ring
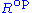 has the same underlying set as R, the addition operation is defined as in R, but the product of s and r in
has the same underlying set as R, the addition operation is defined as in R, but the product of s and r in 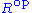 is rs, while the product is sr in R.
is rs, while the product is sr in R.
Polynomial rings
Differential polynomial ringFormal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
ring
Laurent polynomial ring
Monoid ring
Polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
- Given R a commutative ring. The polynomial ring R[x] is defined to be the set
 with addition defined by
with addition defined by 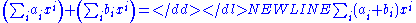 , and with multiplication defined by
, and with multiplication defined by 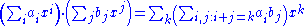 .
.
- Some results about properties of R and R[x]:
- If R is UFD, so is R[x].
- If R is Noetherian, so is R[x].
Ring of rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s
Skew polynomial ring- Given R a ring and an endomorphism
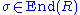 of R. The skew polynomial ring
of R. The skew polynomial ring 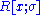 is defined to be the set
is defined to be the set  , with addition defined as usual, and multiplication defined by the relation
, with addition defined as usual, and multiplication defined by the relation 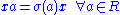 .
.
Miscellaneous
CharacteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
: The characteristic of a ring is the smallest positive integer n satisfying nx=0 for all elements x of the ring, if such an n exists. Otherwise, the characteristic is 0.
Krull dimensionKrull dimensionIn commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
of a commutative ring : The maximal length of a strictly increasing chain of prime ideals in the ring.
Ringlike structures
The following structures include generalizations and other algebraic objects similar to rings.
NearringNearringIn mathematics, a near-ring is an algebraic structure similar to a ring, but that satisfies fewer axioms. Near-rings arise naturally from functions on groups.- Definition :...
: A structure that is a group under addition, a semigroupSemigroupIn mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
under multiplication, and whose multiplication distributes on the right over addition.
RngRng (algebra)In abstract algebra, a rng is an algebraic structure satisfying the same properties as a ring, except that multiplication need not have an identity element...
: An algebraic structure satisfying the same properties as a ring, except that multiplication need not have an identity element. The term "rng" is meant to suggest that it is a "ring" without an "identity".
SemiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
: An algebraic structure satisfying the same properties as a ring, except that addition need only be an abelian monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
operation, rather than an abelian group operation. That is, elements in a semiring need not have additive inverses. - Some results about properties of R and R[x]:

