Glossary of differential geometry and topology
Encyclopedia
This is a glossary
of terms specific to differential geometry and differential topology
.
The following two glossaries are closely related:
See also:
Words in italics denote a self-reference to this glossary.
Cobordism
Codimension
. The codimension of a submanifold is the dimension of the ambient space minus the dimension of the submanifold.
Connected sum
Connection
Cotangent bundle
, the vector bundle of cotangent spaces on a manifold.
Cotangent space
. Given two differentiable manifolds
M and N, a bijective map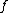
from M to N is called a diffeomorphism if both 
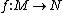and its inverse 
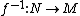are smooth function
s.
Doubling, given a manifold M with boundary, doubling is taking two copies of M and identifying their boundaries.
As the result we get a manifold without boundary.
Fiber bundle
Frame. A frame at a point of a differentiable manifold
M is a basis of the tangent space
at the point.
Frame bundle
, the principal bundle of frames on a smooth manifold.
Flow
. A lens space is a quotient of the 3-sphere
(or (2n + 1)-sphere) by a free isometric action
of Zk
.
. A topological manifold is a locally Euclidean Hausdorff space
. (In Wikipedia, a manifold need not be paracompact or second-countable
.) A Ck manifold is a differentiable manifold whose chart overlap functions are k times continuously differentiable. A C∞ or smooth manifold is a differentiable manifold whose chart overlap functions are infinitely continuously differentiable.
Principal bundle
. A principal bundle is a fiber bundle P → B together with an action
on P by a Lie group
G that preserves the fibers of P and acts simply transitively on those fibers.
Pullback
Submanifold. A submanifold is the image of a smooth embedding of a manifold.
Submersion
Surface
, a two-dimensional manifold or submanifold.
Systole, least length of a noncontractible loop.
, the vector bundle of tangent spaces on a differentiable manifold.
Tangent field, a section of the tangent bundle. Also called a vector field.
Tangent space
Torus
Transversality. Two submanifolds M and N intersect transversally if at each point of intersection p their tangent spaces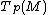
and 
generate the whole tangent space at p of the total manifold.
Trivialization
, a fiber bundle whose fibers are vector spaces and whose transition functions are linear maps.
Vector field
, a section of a vector bundle. More specifically, a vector field can mean a section of the tangent bundle.
is a vector bundle over B ×B. The diagonal map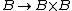
induces a vector bundle over B called the Whitney sum of these vector bundles and denoted by α⊕β.
Glossary
A glossary, also known as an idioticon, vocabulary, or clavis, is an alphabetical list of terms in a particular domain of knowledge with the definitions for those terms...
of terms specific to differential geometry and differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
.
The following two glossaries are closely related:
- Glossary of general topology
- Glossary of Riemannian and metric geometryGlossary of Riemannian and metric geometryThis is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology....
.
See also:
Words in italics denote a self-reference to this glossary.
C
ChartCobordism
Cobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
Codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
. The codimension of a submanifold is the dimension of the ambient space minus the dimension of the submanifold.
Connected sum
Connected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
Connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
Cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
, the vector bundle of cotangent spaces on a manifold.
Cotangent space
Cotangent space
In differential geometry, one can attach to every point x of a smooth manifold a vector space called the cotangent space at x. Typically, the cotangent space is defined as the dual space of the tangent space at x, although there are more direct definitions...
D
DiffeomorphismDiffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
. Given two differentiable manifolds
M and N, a bijective map
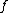from M to N is called a diffeomorphism if both 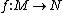and its inverse 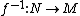are smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s.
Doubling, given a manifold M with boundary, doubling is taking two copies of M and identifying their boundaries.
As the result we get a manifold without boundary.
F
Fiber. In a fiber bundle, π: E → B the preimage π−1(x) of a point x in the base B is called the fiber over x, often denoted Ex.Fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
Frame. A frame at a point of a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
M is a basis of the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at the point.
Frame bundle
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
, the principal bundle of frames on a smooth manifold.
Flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
L
Lens spaceLens space
A lens space is an example of a topological space, considered in mathematics. The term often refers to a specific class of 3-manifolds, but in general can be defined for higher dimensions....
. A lens space is a quotient of the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
(or (2n + 1)-sphere) by a free isometric action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of Zk
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
.
M
ManifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. A topological manifold is a locally Euclidean Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. (In Wikipedia, a manifold need not be paracompact or second-countable
Second-countable space
In topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
.) A Ck manifold is a differentiable manifold whose chart overlap functions are k times continuously differentiable. A C∞ or smooth manifold is a differentiable manifold whose chart overlap functions are infinitely continuously differentiable.
P
Parallelizable. A smooth manifold is parallelizable if it admits a smooth global frame. This is equivalent to the tangent bundle being trivial.Principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
. A principal bundle is a fiber bundle P → B together with an action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on P by a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G that preserves the fibers of P and acts simply transitively on those fibers.
Pullback
Pullback
Suppose that φ:M→ N is a smooth map between smooth manifolds M and N; then there is an associated linear map from the space of 1-forms on N to the space of 1-forms on M. This linear map is known as the pullback , and is frequently denoted by φ*...
S
SectionSection (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
Submanifold. A submanifold is the image of a smooth embedding of a manifold.
Submersion
Submersion (mathematics)
In mathematics, a submersion is a differentiable map between differentiable manifolds whose differential is everywhere surjective. This is a basic concept in differential topology...
Surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
, a two-dimensional manifold or submanifold.
Systole, least length of a noncontractible loop.
T
Tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
, the vector bundle of tangent spaces on a differentiable manifold.
Tangent field, a section of the tangent bundle. Also called a vector field.
Tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
Torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
Transversality. Two submanifolds M and N intersect transversally if at each point of intersection p their tangent spaces
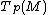and generate the whole tangent space at p of the total manifold.Trivialization
V
Vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
, a fiber bundle whose fibers are vector spaces and whose transition functions are linear maps.
Vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
, a section of a vector bundle. More specifically, a vector field can mean a section of the tangent bundle.
W
Whitney sum. A Whitney sum is an analog of the direct product for vector bundles. Given two vector bundles α and β over the same base B their cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
is a vector bundle over B ×B. The diagonal map
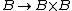induces a vector bundle over B called the Whitney sum of these vector bundles and denoted by α⊕β.