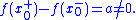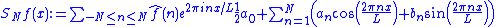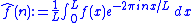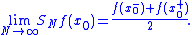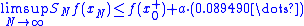
Gibbs phenomenon
Encyclopedia
In mathematics
, the Gibbs phenomenon, named after the American physicist J. Willard Gibbs, is the peculiar manner in which the Fourier series
of a piecewise
continuously differentiable periodic function
behaves at a jump discontinuity: the nth partial sum of the Fourier series has large oscillations near the jump, which might increase the maximum of the partial sum above that of the function itself. The overshoot does not die out as the frequency
increases, but approaches a finite limit.
These are one cause of ringing artifacts
in signal processing
.
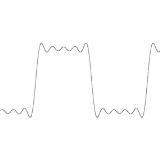
The three pictures on the right demonstrate the phenomenon for a square wave
whose Fourier expansion is

More precisely, this is the function f which equals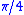 between
between 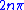 and
and 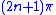 and
and 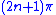 between
between  and
and 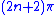 for every integer
for every integer
n; thus this square wave has a jump discontinuity of height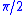 at every integer multiple of
at every integer multiple of  .
.
As can be seen, as the number of terms rises, the error of the approximation is reduced in width and energy, but converges to a fixed height. A calculation for the square wave (see Zygmund, chap. 8.5., or the computations at the end of this article) gives an explicit formula for the limit of the height of the error. It turns out that the Fourier series exceeds the height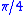 of the square wave by
of the square wave by
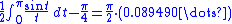
or about 9 percent. More generally, at any jump point of a piecewise continuously differentiable function with a jump of a, the nth partial Fourier series will (for n very large) overshoot this jump by approximately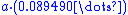 at one end and undershoot it by the same amount at the other end; thus the "jump" in the partial Fourier series will be about 18% larger than the jump in the original function. At the location of the discontinuity itself, the partial Fourier series will converge to the midpoint of the jump (regardless of what the actual value of the original function is at this point). The quantity
at one end and undershoot it by the same amount at the other end; thus the "jump" in the partial Fourier series will be about 18% larger than the jump in the original function. At the location of the discontinuity itself, the partial Fourier series will converge to the midpoint of the jump (regardless of what the actual value of the original function is at this point). The quantity
is sometimes known as the Wilbraham
–Gibbs constant.
. He published a paper on it in 1848 that went unnoticed by the mathematical world. It was not until Albert Michelson observed the phenomenon via a mechanical graphing machine that interest arose. Michelson developed a device in 1898 that could compute and re-synthesize the Fourier series. When the Fourier coefficients for a square wave were input to the machine, the graph would oscillate at the discontinuities. This would continue to occur even as the number of Fourier coefficient
s increased.
Because it was a physical device subject to manufacturing flaws, Michelson was convinced that the overshoot was caused by errors in the machine. In 1898 J. Willard Gibbs published a paper on Fourier series in which he discussed the example of what today would be called a sawtooth wave
, and described the graph obtained as a limit of the graphs of the partial sums of the Fourier series. Interestingly in this paper he failed to notice the phenomenon that bears his name, and the limit he described was incorrect. In 1899 he published a correction to his paper in which he describes the phenomenon and points out the important distinction between the limit of the graphs and the graph of the function that is the limit of the partial sums of the Fourier series (Nature: April 27, 1899, p.606). Maxime Bôcher
gave a detailed mathematical analysis of the phenomenon in 1906 and named it the Gibbs phenomenon.
sine and cosine waves. It is important to put emphasis on the word finite because even though every partial sum of the Fourier series overshoots the function it is approximating, the limit of the partial sums does not. The value of x where the maximum overshoot is achieved moves closer and closer to the discontinuity as the number of terms summed increases so, again informally, once the overshoot has passed by a particular x, convergence at the value of x is possible.
There is no contradiction in the overshoot converging to a non-zero amount, but the limit of the partial sums having no overshoot, because where that overshoot happens moves. We have pointwise convergence, but not uniform convergence. For a piecewise C1 function the Fourier series converges to the function at every point except at the jump discontinuities. At the jump discontinuities themselves the limit will converge to the average of the values of the function on either side of the jump. This is a consequence of the Dirichlet theorem
.
The Gibbs phenomenon is also closely related to the principle that the decay of the Fourier coefficients of a function at infinity is controlled by the smoothness of that function; very smooth functions will have very rapidly decaying Fourier coefficients (resulting in the rapid convergence of the Fourier series), whereas discontinuous functions will have very slowly decaying Fourier coefficients (causing the Fourier series to converge very slowly). Note for instance that the Fourier coefficients 1, −1/3, 1/5, ... of the discontinuous square wave described above decay only as fast as the harmonic series
, which is not absolutely convergent; indeed, the above Fourier series turns out to be only conditionally convergent for almost every
value of x. This provides a partial explanation of the Gibbs phenomenon, since Fourier series with absolutely convergent Fourier coefficients would be uniformly convergent by the Weierstrass M-test and would thus be unable to exhibit the above oscillatory behavior. By the same token, it
is impossible for a discontinuous function to have absolutely convergent Fourier coefficients, since the function would thus be the uniform limit of continuous functions and therefore be continuous, a contradiction. See more about absolute convergence of Fourier series.
transform with Haar basis functions, the Gibbs phenomenon does not occur.
 be a piecewise continuously differentiable function which is periodic with some period
be a piecewise continuously differentiable function which is periodic with some period  . Suppose that at some point
. Suppose that at some point  , the left limit
, the left limit 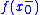 and right limit
and right limit 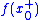 of the function
of the function 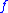 differ by a non-zero gap
differ by a non-zero gap  :
:
For each positive integer N ≥ 1, let SN f be the Nth partial Fourier series
where the Fourier coefficients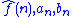 are given by the usual formulae
are given by the usual formulae
Then we have
and
but
More generally, if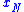 is any sequence of real numbers which converges to
is any sequence of real numbers which converges to  as
as  , and if the gap a is positive then
, and if the gap a is positive then
and
If instead the gap a is negative, one needs to interchange limit superior with limit inferior, and also interchange
the ≤ and ≥ signs, in the above two inequalities.
.svg.png) From the point of view of signal processing
From the point of view of signal processing
, the Gibbs phenomenon is the step response
of a low-pass filter
, and the oscillations are called ringing
or ringing artifacts
. Truncating the Fourier transform
of a signal on the real line, or the Fourier series of a periodic signal (equivalently, a signal on the circle) corresponds to filtering out the higher frequencies by an ideal (brick-wall) low-pass/high-cut filter. This can be represented as convolution
of the original signal with the impulse response
of the filter (also known as the kernel), which is the sinc function. Thus the Gibbs phenomenon can be seen as the result of convolving a Heaviside step function
(if periodicity is not required) or a square wave
(if periodic) with a sinc function: the oscillations in the sinc function cause the ripples in the output.
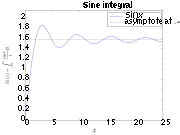 In the case of convolving with a Heaviside step function, the resulting function is exactly the integral of the sinc function, the sine integral; for a square wave the description is not as simply stated. For the step function, the magnitude of the undershoot is thus exactly the integral of the (left) tail, integrating to the first negative zero: for the normalized sinc of unit sampling period, this is
In the case of convolving with a Heaviside step function, the resulting function is exactly the integral of the sinc function, the sine integral; for a square wave the description is not as simply stated. For the step function, the magnitude of the undershoot is thus exactly the integral of the (left) tail, integrating to the first negative zero: for the normalized sinc of unit sampling period, this is 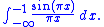 The overshoot is accordingly of the same magnitude: the integral of the right tail, or, which amounts to the same thing, the difference between the integral from negative infinity to the first positive zero, minus 1 (the non-overshooting value).
The overshoot is accordingly of the same magnitude: the integral of the right tail, or, which amounts to the same thing, the difference between the integral from negative infinity to the first positive zero, minus 1 (the non-overshooting value).
The overshoot and undershoot can be understood thus: kernels are generally normalized to have integral 1, so they result in a mapping of constant functions to constant functions – otherwise they have gain
. The value of a convolution at a point is a linear combination
of the input signal, with coefficients (weights) the values of the kernel.
If a kernel is non-negative, such as for a Gaussian kernel, then the value of the filtered signal will be a convex combination
of the input values (the coefficients (the kernel) integrate to 1, and are non-negative), and will thus fall between the minimum and maximum of the input signal – it will not undershoot or overshoot. If, on the other hand, the kernel assumes negative values, such as the sinc function, then the value of the filtered signal will instead be an affine combination of the input values, and may fall outside of the minimum and maximum of the input signal, resulting in undershoot and overshoot, as in the Gibbs phenomenon.
Taking a longer expansion – cutting at a higher frequency – corresponds in the frequency domain to widening the brick-wall, which in the time domain corresponds to narrowing the sinc function and increasing its height by the same factor, leaving the integrals between corresponding points unchanged. This is a general feature of the Fourier transform: widening in one domain corresponds to narrowing and increasing height in the other. This results in the oscillations in sinc being narrower and taller and, in the filtered function (after convolution), yields oscillations that are narrower and thus have less area, but does not reduce the magnitude: cutting off at any finite frequency results in a sinc function, however narrow, with the same tail integrals. This explains the persistence of the overshoot and undershoot.
Thus the features of the Gibbs phenomenon are interpreted as follows:
 , the discontinuity
, the discontinuity  is at zero, and the jump a is equal to
is at zero, and the jump a is equal to 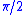 .
.
For simplicity let us just deal with the case when N is even (the case of odd N is very similar). Then
we have
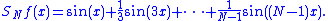
Substituting , we obtain
, we obtain
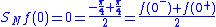
as claimed above. Next, we compute

If we introduce the normalized sinc function,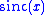 , we can rewrite this as
, we can rewrite this as

But the expression in square brackets is a numerical integration
approximation to the integral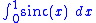 (more precisely, it is a midpoint rule approximation with spacing
(more precisely, it is a midpoint rule approximation with spacing  ). Since the sinc function is continuous, this approximation converges to the actual integral
). Since the sinc function is continuous, this approximation converges to the actual integral
as . Thus we have
. Thus we have
which was what was claimed in the previous section. A similar computation shows
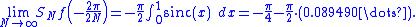
from the overshoot and undershoot, and ringing artifacts
from the oscillations. In the case of low-pass filtering, these can be reduced or eliminated by using different low-pass filters.
In MRI, the Gibbs phenomenon causes artifacts in the presence of adjacent regions of markedly differing signal intensity. This is most commonly encountered in spinal MR imaging, where the Gibbs phenomenon may simulate the appearance of syringomyelia
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Gibbs phenomenon, named after the American physicist J. Willard Gibbs, is the peculiar manner in which the Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
of a piecewise
Piecewise
On mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...
continuously differentiable periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
behaves at a jump discontinuity: the nth partial sum of the Fourier series has large oscillations near the jump, which might increase the maximum of the partial sum above that of the function itself. The overshoot does not die out as the frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
increases, but approaches a finite limit.
These are one cause of ringing artifacts
Ringing (signal)
In electronics, signal processing, and video, ringing is unwanted oscillation of a signal, particularly in the step response...
in signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
.
Description
The Gibbs phenomenon involves both the fact that Fourier sums overshoot at a jump discontinuity, and that this overshoot does not die out as the frequency increases.The three pictures on the right demonstrate the phenomenon for a square wave
Square wave
A square wave is a kind of non-sinusoidal waveform, most typically encountered in electronics and signal processing. An ideal square wave alternates regularly and instantaneously between two levels...
whose Fourier expansion is

More precisely, this is the function f which equals
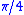 between
between 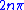 and
and 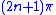 and
and 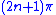 between
between  and
and 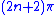 for every integer
for every integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n; thus this square wave has a jump discontinuity of height
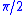 at every integer multiple of
at every integer multiple of  .
.As can be seen, as the number of terms rises, the error of the approximation is reduced in width and energy, but converges to a fixed height. A calculation for the square wave (see Zygmund, chap. 8.5., or the computations at the end of this article) gives an explicit formula for the limit of the height of the error. It turns out that the Fourier series exceeds the height
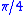 of the square wave by
of the square wave by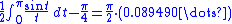
or about 9 percent. More generally, at any jump point of a piecewise continuously differentiable function with a jump of a, the nth partial Fourier series will (for n very large) overshoot this jump by approximately
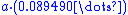 at one end and undershoot it by the same amount at the other end; thus the "jump" in the partial Fourier series will be about 18% larger than the jump in the original function. At the location of the discontinuity itself, the partial Fourier series will converge to the midpoint of the jump (regardless of what the actual value of the original function is at this point). The quantity
at one end and undershoot it by the same amount at the other end; thus the "jump" in the partial Fourier series will be about 18% larger than the jump in the original function. At the location of the discontinuity itself, the partial Fourier series will converge to the midpoint of the jump (regardless of what the actual value of the original function is at this point). The quantity
is sometimes known as the Wilbraham
Henry Wilbraham
Henry Wilbraham was an obscure English mathematician. His only noteworthy accomplishment was discovering and explaining the Gibbs phenomenon nearly fifty years before J. Willard Gibbs did...
–Gibbs constant.
History
The Gibbs phenomenon was first noticed and analyzed by the obscure Henry WilbrahamHenry Wilbraham
Henry Wilbraham was an obscure English mathematician. His only noteworthy accomplishment was discovering and explaining the Gibbs phenomenon nearly fifty years before J. Willard Gibbs did...
. He published a paper on it in 1848 that went unnoticed by the mathematical world. It was not until Albert Michelson observed the phenomenon via a mechanical graphing machine that interest arose. Michelson developed a device in 1898 that could compute and re-synthesize the Fourier series. When the Fourier coefficients for a square wave were input to the machine, the graph would oscillate at the discontinuities. This would continue to occur even as the number of Fourier coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s increased.
Because it was a physical device subject to manufacturing flaws, Michelson was convinced that the overshoot was caused by errors in the machine. In 1898 J. Willard Gibbs published a paper on Fourier series in which he discussed the example of what today would be called a sawtooth wave
Sawtooth wave
The sawtooth wave is a kind of non-sinusoidal waveform. It is named a sawtooth based on its resemblance to the teeth on the blade of a saw....
, and described the graph obtained as a limit of the graphs of the partial sums of the Fourier series. Interestingly in this paper he failed to notice the phenomenon that bears his name, and the limit he described was incorrect. In 1899 he published a correction to his paper in which he describes the phenomenon and points out the important distinction between the limit of the graphs and the graph of the function that is the limit of the partial sums of the Fourier series (Nature: April 27, 1899, p.606). Maxime Bôcher
Maxime Bôcher
Maxime Bôcher was an American mathematician who published about 100 papers on differential equations, series, and algebra. He also wrote elementary texts such as Trigonometry and Analytic Geometry. Bôcher's theorem, Bôcher's equation, and the Bôcher Memorial Prize are named after him.-Life:Bôcher...
gave a detailed mathematical analysis of the phenomenon in 1906 and named it the Gibbs phenomenon.
Explanation
Informally, it reflects the difficulty inherent in approximating a discontinuous function by a finite series of continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
sine and cosine waves. It is important to put emphasis on the word finite because even though every partial sum of the Fourier series overshoots the function it is approximating, the limit of the partial sums does not. The value of x where the maximum overshoot is achieved moves closer and closer to the discontinuity as the number of terms summed increases so, again informally, once the overshoot has passed by a particular x, convergence at the value of x is possible.
There is no contradiction in the overshoot converging to a non-zero amount, but the limit of the partial sums having no overshoot, because where that overshoot happens moves. We have pointwise convergence, but not uniform convergence. For a piecewise C1 function the Fourier series converges to the function at every point except at the jump discontinuities. At the jump discontinuities themselves the limit will converge to the average of the values of the function on either side of the jump. This is a consequence of the Dirichlet theorem
Dirichlet conditions
In mathematics, the Dirichlet conditions are sufficient conditions for a real-valued, periodic function f to be equal to the sum of its Fourier series at each point where f is continuous. Moreover, the behavior of the Fourier series at points of discontinuity is determined as well...
.
The Gibbs phenomenon is also closely related to the principle that the decay of the Fourier coefficients of a function at infinity is controlled by the smoothness of that function; very smooth functions will have very rapidly decaying Fourier coefficients (resulting in the rapid convergence of the Fourier series), whereas discontinuous functions will have very slowly decaying Fourier coefficients (causing the Fourier series to converge very slowly). Note for instance that the Fourier coefficients 1, −1/3, 1/5, ... of the discontinuous square wave described above decay only as fast as the harmonic series
Harmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
, which is not absolutely convergent; indeed, the above Fourier series turns out to be only conditionally convergent for almost every
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
value of x. This provides a partial explanation of the Gibbs phenomenon, since Fourier series with absolutely convergent Fourier coefficients would be uniformly convergent by the Weierstrass M-test and would thus be unable to exhibit the above oscillatory behavior. By the same token, it
is impossible for a discontinuous function to have absolutely convergent Fourier coefficients, since the function would thus be the uniform limit of continuous functions and therefore be continuous, a contradiction. See more about absolute convergence of Fourier series.
Solutions
In practice, the difficulties associated with the Gibbs phenomenon can be ameliorated by using a smoother method of Fourier series summation, such as Fejér summation or Riesz summation, or by using sigma-approximation. Using a waveletWavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
transform with Haar basis functions, the Gibbs phenomenon does not occur.
Formal mathematical description of the phenomenon
Let be a piecewise continuously differentiable function which is periodic with some period
be a piecewise continuously differentiable function which is periodic with some period  . Suppose that at some point
. Suppose that at some point  , the left limit
, the left limit 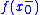 and right limit
and right limit 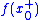 of the function
of the function 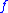 differ by a non-zero gap
differ by a non-zero gap  :
:For each positive integer N ≥ 1, let SN f be the Nth partial Fourier series
where the Fourier coefficients
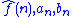 are given by the usual formulae
are given by the usual formulaeThen we have
and
but
More generally, if
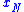 is any sequence of real numbers which converges to
is any sequence of real numbers which converges to  as
as  , and if the gap a is positive then
, and if the gap a is positive then
and
If instead the gap a is negative, one needs to interchange limit superior with limit inferior, and also interchange
the ≤ and ≥ signs, in the above two inequalities.
Signal processing explanation
.svg.png)
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, the Gibbs phenomenon is the step response
Step response
The step response of a system in a given initial state consists of the time evolution of its outputs when its control inputs are Heaviside step functions. In electronic engineering and control theory, step response is the time behaviour of the outputs of a general system when its inputs change from...
of a low-pass filter
Low-pass filter
A low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
, and the oscillations are called ringing
Ringing (signal)
In electronics, signal processing, and video, ringing is unwanted oscillation of a signal, particularly in the step response...
or ringing artifacts
Ringing artifacts
In signal processing, particularly digital image processing, ringing artifacts are artifacts that appear as spurious signals near sharp transitions in a signal. Visually, they appear as bands or "ghosts" near edges; audibly, they appear as "echos" near transients, particularly sounds from...
. Truncating the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of a signal on the real line, or the Fourier series of a periodic signal (equivalently, a signal on the circle) corresponds to filtering out the higher frequencies by an ideal (brick-wall) low-pass/high-cut filter. This can be represented as convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of the original signal with the impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
of the filter (also known as the kernel), which is the sinc function. Thus the Gibbs phenomenon can be seen as the result of convolving a Heaviside step function
Heaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
(if periodicity is not required) or a square wave
Square wave
A square wave is a kind of non-sinusoidal waveform, most typically encountered in electronics and signal processing. An ideal square wave alternates regularly and instantaneously between two levels...
(if periodic) with a sinc function: the oscillations in the sinc function cause the ripples in the output.

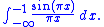 The overshoot is accordingly of the same magnitude: the integral of the right tail, or, which amounts to the same thing, the difference between the integral from negative infinity to the first positive zero, minus 1 (the non-overshooting value).
The overshoot is accordingly of the same magnitude: the integral of the right tail, or, which amounts to the same thing, the difference between the integral from negative infinity to the first positive zero, minus 1 (the non-overshooting value).The overshoot and undershoot can be understood thus: kernels are generally normalized to have integral 1, so they result in a mapping of constant functions to constant functions – otherwise they have gain
Gain
In electronics, gain is a measure of the ability of a circuit to increase the power or amplitude of a signal from the input to the output. It is usually defined as the mean ratio of the signal output of a system to the signal input of the same system. It may also be defined on a logarithmic scale,...
. The value of a convolution at a point is a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the input signal, with coefficients (weights) the values of the kernel.
If a kernel is non-negative, such as for a Gaussian kernel, then the value of the filtered signal will be a convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
of the input values (the coefficients (the kernel) integrate to 1, and are non-negative), and will thus fall between the minimum and maximum of the input signal – it will not undershoot or overshoot. If, on the other hand, the kernel assumes negative values, such as the sinc function, then the value of the filtered signal will instead be an affine combination of the input values, and may fall outside of the minimum and maximum of the input signal, resulting in undershoot and overshoot, as in the Gibbs phenomenon.
Taking a longer expansion – cutting at a higher frequency – corresponds in the frequency domain to widening the brick-wall, which in the time domain corresponds to narrowing the sinc function and increasing its height by the same factor, leaving the integrals between corresponding points unchanged. This is a general feature of the Fourier transform: widening in one domain corresponds to narrowing and increasing height in the other. This results in the oscillations in sinc being narrower and taller and, in the filtered function (after convolution), yields oscillations that are narrower and thus have less area, but does not reduce the magnitude: cutting off at any finite frequency results in a sinc function, however narrow, with the same tail integrals. This explains the persistence of the overshoot and undershoot.
Thus the features of the Gibbs phenomenon are interpreted as follows:
- the undershoot is due to the impulse response having a negative tail integral, which is possible because the function takes negative values;
- the overshoot offsets this, by symmetry (the overall integral does not change under filtering);
- the persistence of the oscillations is because increasing the cutoff narrows the impulse response, but does not reduce its integral – the oscillations thus move towards the discontinuity, but do not decrease in magnitude.
The square wave example
We now illustrate the above Gibbs phenomenon in the case of the square wave described earlier. In this case the period L is , the discontinuity
, the discontinuity  is at zero, and the jump a is equal to
is at zero, and the jump a is equal to 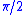 .
.For simplicity let us just deal with the case when N is even (the case of odd N is very similar). Then
we have
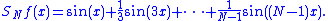
Substituting
 , we obtain
, we obtain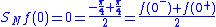
as claimed above. Next, we compute

If we introduce the normalized sinc function,
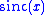 , we can rewrite this as
, we can rewrite this as
But the expression in square brackets is a numerical integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
approximation to the integral
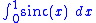 (more precisely, it is a midpoint rule approximation with spacing
(more precisely, it is a midpoint rule approximation with spacing  ). Since the sinc function is continuous, this approximation converges to the actual integral
). Since the sinc function is continuous, this approximation converges to the actual integralas
 . Thus we have
. Thus we have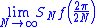 |
 |
 |
|
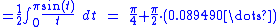 |
which was what was claimed in the previous section. A similar computation shows
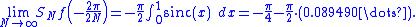
Consequences
In signal processing, the Gibbs phenomenon is undesirable because it causes artifacts, namely clippingClipping (audio)
Clipping is a form of waveform distortion that occurs when an amplifier is overdriven and attempts to deliver an output voltage or current beyond its maximum capability...
from the overshoot and undershoot, and ringing artifacts
Ringing artifacts
In signal processing, particularly digital image processing, ringing artifacts are artifacts that appear as spurious signals near sharp transitions in a signal. Visually, they appear as bands or "ghosts" near edges; audibly, they appear as "echos" near transients, particularly sounds from...
from the oscillations. In the case of low-pass filtering, these can be reduced or eliminated by using different low-pass filters.
In MRI, the Gibbs phenomenon causes artifacts in the presence of adjacent regions of markedly differing signal intensity. This is most commonly encountered in spinal MR imaging, where the Gibbs phenomenon may simulate the appearance of syringomyelia
Syringomyelia
Syringomyelia is a generic term referring to a disorder in which a cyst or cavity forms within the spinal cord. This cyst, called a syrinx, can expand and elongate over time, destroying the spinal cord. The damage may result in pain, paralysis, weakness, and stiffness in the back, shoulders, and...
.
See also
- Compare with Runge's phenomenonRunge's phenomenonIn the mathematical field of numerical analysis, Runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using polynomial interpolation with polynomials of high degree...
for polynomial approximations - Sigma approximationSigma approximationIn mathematics, σ-approximation adjusts a Fourier summation to eliminate the Gibbs phenomenon which would otherwise occur at discontinuities.A σ-approximated summation for a series of period T can be written as follows:...
- Sine integral
- Henry WilbrahamHenry WilbrahamHenry Wilbraham was an obscure English mathematician. His only noteworthy accomplishment was discovering and explaining the Gibbs phenomenon nearly fifty years before J. Willard Gibbs did...
External links and references
- Weisstein, Eric W., "Gibbs Phenomenon". From MathWorld—A Wolfram Web Resource.
- Prandoni, Paolo, "Gibbs Phenomenon".
- Radaelli-Sanchez, Ricardo, and Richard Baraniuk, "Gibbs Phenomenon". The Connexions Project. (Creative Commons Attribution License)
- Horatio S Carslaw : Introduction to the theory of Fourier's series and integrals.pdf (introductiontot00unkngoog.pdf ) at archive.org