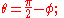Geographical distance
Encyclopedia
Geographical distance is the distance
measured along the surface of the earth
. The formulae in this article calculate distances between points which are defined by geographical coordinates in terms of latitude
and longitude
.
All abstractions above ignore changes in elevation. Calculation of distances which account for changes in elevation relative to the idealized surface are not discussed in this article.
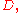 is calculated between two points,
is calculated between two points, 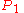 and
and 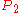 . The geographical coordinates of the two points, as (latitude, longitude) pairs, are
. The geographical coordinates of the two points, as (latitude, longitude) pairs, are 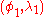 and
and 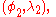 respectively. Which of the two points is designated as
respectively. Which of the two points is designated as 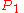 is not important for the calculation of distance.
is not important for the calculation of distance.
Latitude and longitude coordinates on maps are usually expressed in degree
s. In the given forms of the formulae below, one or more values must be expressed in the specified units to obtain the correct result. Where geographic coordinates are used as the argument of a trigonometric function, the values may be expressed in any angular units compatible with the method used to determine the value of the trigonometric function. Many electronic calculators allow calculations of trigonometric functions in either degrees or radian
s. The calculator mode must be compatible with the units used for geometric coordinates.
Differences in latitude and longitude are labeled and calculated as follows: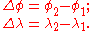
It is not important whether the result is positive or negative when used in the formulae below.
"Mean latitude" is labeled and calculated as follows: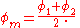
Colatitude is labeled and calculated as follows:
Unless specified otherwise, the radius
of the earth for the calculations below is: = 6,371.009 kilometers = 3,958.761 statute miles = 3,440.069 nautical mile
= 6,371.009 kilometers = 3,958.761 statute miles = 3,440.069 nautical mile
s.
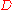 = Distance between the two points, as measured along the surface of the earth and in the same units as the value used for radius unless specified otherwise.
= Distance between the two points, as measured along the surface of the earth and in the same units as the value used for radius unless specified otherwise.
at the Poles
(longitude is undefined) and a discontinuity at the ±180° meridian
. Also, planar projections of the circles of constant latitude
are highly curved near the Poles. Hence, the above equations for delta
latitude/longitude (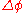 ,
, 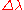 ) and mean latitude (
) and mean latitude (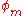 ) may not give the expected answer for positions near the Poles or the ±180° meridian. Consider e.g. the value of
) may not give the expected answer for positions near the Poles or the ±180° meridian. Consider e.g. the value of 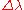 (“east displacement”) when
(“east displacement”) when 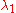 and
and 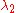 are on either side of the ±180° meridian, or the value of
are on either side of the ±180° meridian, or the value of 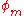 (“mean latitude”) for the two positions (
(“mean latitude”) for the two positions (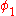 =89°,
=89°, 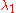 =45°) and (
=45°) and (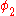 =89°,
=89°, 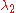 =−135°).
=−135°).
An incident caused by inappropriate handling of the discontinuity was the software crash of twelve F-22 Raptor
s when crossing the ±180° meridian. If a calculation based on latitude/longitude should be valid for all Earth positions, it should be verified that the discontinuity and the Poles are handled correctly. Another solution is to use n-vector
instead of latitude/longitude, since this representation
does not have discontinuities or singularities.
The shortest distance between two points in plane is a straight line. The Pythagorean theorem
is used to calculate the distance between points in a plane.
Even over short distances, the accuracy of geographic distance calculations which assume a flat Earth depend on the method by which the latitude and longitude coordinates have been projected onto the plane. The projection of global latitude and longitude coordinates onto a plane is the realm of cartography
.
The formulae presented in this section provide varying degrees of accuracy.

prescribes essentially the following formulae in 47 CFR 73.208 for distances not exceeding 475 km /295 miles:

Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
measured along the surface of the earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
. The formulae in this article calculate distances between points which are defined by geographical coordinates in terms of latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
and longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
.
An abstraction
Calculating the distance between geographical coordinates is based on some level of abstraction; it does not provide an exact distance, which is unattainable if one attempted to account for every irregularity in the surface of the earth. Common abstractions for the surface between two geographic points are:- Flat surface;
- Spherical surface;
- Ellipsoidal surface.
All abstractions above ignore changes in elevation. Calculation of distances which account for changes in elevation relative to the idealized surface are not discussed in this article.
Nomenclature
Distance,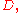 is calculated between two points,
is calculated between two points, 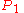 and
and 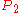 . The geographical coordinates of the two points, as (latitude, longitude) pairs, are
. The geographical coordinates of the two points, as (latitude, longitude) pairs, are 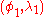 and
and 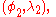 respectively. Which of the two points is designated as
respectively. Which of the two points is designated as 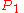 is not important for the calculation of distance.
is not important for the calculation of distance.Latitude and longitude coordinates on maps are usually expressed in degree
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
s. In the given forms of the formulae below, one or more values must be expressed in the specified units to obtain the correct result. Where geographic coordinates are used as the argument of a trigonometric function, the values may be expressed in any angular units compatible with the method used to determine the value of the trigonometric function. Many electronic calculators allow calculations of trigonometric functions in either degrees or radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s. The calculator mode must be compatible with the units used for geometric coordinates.
Differences in latitude and longitude are labeled and calculated as follows:
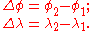
It is not important whether the result is positive or negative when used in the formulae below.
"Mean latitude" is labeled and calculated as follows:
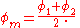
Colatitude is labeled and calculated as follows:
- For latitudes expressed in radians:
- For latitudes expressed in degrees:
Unless specified otherwise, the radius
Earth radius
Because the Earth is not perfectly spherical, no single value serves as its natural radius. Distances from points on the surface to the center range from 6,353 km to 6,384 km...
of the earth for the calculations below is:
 = 6,371.009 kilometers = 3,958.761 statute miles = 3,440.069 nautical mile
= 6,371.009 kilometers = 3,958.761 statute miles = 3,440.069 nautical mileNautical mile
The nautical mile is a unit of length that is about one minute of arc of latitude along any meridian, but is approximately one minute of arc of longitude only at the equator...
s.
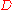 = Distance between the two points, as measured along the surface of the earth and in the same units as the value used for radius unless specified otherwise.
= Distance between the two points, as measured along the surface of the earth and in the same units as the value used for radius unless specified otherwise.Singularities and discontinuity of latitude/longitude
Longitude has singularitiesMathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
at the Poles
Geographical pole
A geographical pole is either of the two points—the north pole and the south pole—on the surface of a rotating planet where the axis of rotation meets the surface of the body...
(longitude is undefined) and a discontinuity at the ±180° meridian
180th meridian
The 180th meridian or antimeridian is the meridian which is 180° east or west of the Prime Meridian passing through the Royal Observatory, Greenwich. It is common to both east longitude and west longitude. It is used as the basis for the International Date Line because it for the most part passes...
. Also, planar projections of the circles of constant latitude
Circle of latitude
A circle of latitude, on the Earth, is an imaginary east-west circle connecting all locations that share a given latitude...
are highly curved near the Poles. Hence, the above equations for delta
Delta (letter)
Delta is the fourth letter of the Greek alphabet. In the system of Greek numerals it has a value of 4. It was derived from the Phoenician letter Dalet...
latitude/longitude (
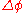 ,
, 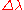 ) and mean latitude (
) and mean latitude (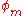 ) may not give the expected answer for positions near the Poles or the ±180° meridian. Consider e.g. the value of
) may not give the expected answer for positions near the Poles or the ±180° meridian. Consider e.g. the value of 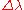 (“east displacement”) when
(“east displacement”) when 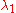 and
and 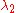 are on either side of the ±180° meridian, or the value of
are on either side of the ±180° meridian, or the value of 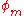 (“mean latitude”) for the two positions (
(“mean latitude”) for the two positions (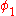 =89°,
=89°, 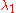 =45°) and (
=45°) and (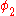 =89°,
=89°, 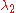 =−135°).
=−135°).An incident caused by inappropriate handling of the discontinuity was the software crash of twelve F-22 Raptor
F-22 Raptor
The Lockheed Martin/Boeing F-22 Raptor is a single-seat, twin-engine fifth-generation supermaneuverable fighter aircraft that uses stealth technology. It was designed primarily as an air superiority fighter, but has additional capabilities that include ground attack, electronic warfare, and signals...
s when crossing the ±180° meridian. If a calculation based on latitude/longitude should be valid for all Earth positions, it should be verified that the discontinuity and the Poles are handled correctly. Another solution is to use n-vector
N-vector
n-vector is a three parameter non-singular horizontal position representation well-suited for replacing latitude and longitude in mathematical calculations and computer algorithms. Geometrically, it is a unit vector that is normal to the reference ellipsoid. The vector is decomposed in an Earth...
instead of latitude/longitude, since this representation
Horizontal position representation
A position representation is the parameters used to express a position relative to a reference. Representing position in three dimensions is often done by a Euclidean vector. However, when representing position relative to the Earth it is often more convenient to represent vertical position as...
does not have discontinuities or singularities.
Flat-surface formulae
A planar approximation for the surface of the earth may be useful over small distances. The accuracy of distance calculations using this approximation become increasingly inaccurate as:- The separation between the points becomes greater;
- A point becomes closer to a geographic pole.
The shortest distance between two points in plane is a straight line. The Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
is used to calculate the distance between points in a plane.
Even over short distances, the accuracy of geographic distance calculations which assume a flat Earth depend on the method by which the latitude and longitude coordinates have been projected onto the plane. The projection of global latitude and longitude coordinates onto a plane is the realm of cartography
Cartography
Cartography is the study and practice of making maps. Combining science, aesthetics, and technique, cartography builds on the premise that reality can be modeled in ways that communicate spatial information effectively.The fundamental problems of traditional cartography are to:*Set the map's...
.
The formulae presented in this section provide varying degrees of accuracy.
Spherical Earth projected to a plane
This formula takes into account the variation in distance between meridians with latitude:
- where:
 and
and  are in radians;
are in radians; must be in units compatible with the method used for determining
must be in units compatible with the method used for determining 
- To change convert latitude or longitude to radians use
- Note: This approximation is very fast and produces fairly accurate result for small distances . Also, when ordering locations by distance, such as in a database query, it is much faster to order by squared distance, eliminating the need for computing the square root.
Ellipsoidal Earth projected to a plane
The FCCFederal Communications Commission
The Federal Communications Commission is an independent agency of the United States government, created, Congressional statute , and with the majority of its commissioners appointed by the current President. The FCC works towards six goals in the areas of broadband, competition, the spectrum, the...
prescribes essentially the following formulae in 47 CFR 73.208 for distances not exceeding 475 km /295 miles:

- where
 = Distance in kilometers;
= Distance in kilometers; and
and  are in degrees;
are in degrees; must be in units compatible with the method used for determining
must be in units compatible with the method used for determining 

- It may be interesting to note that:
 = kilometers per degree of latitude difference;
= kilometers per degree of latitude difference; = kilometers per degree of longitude difference;
= kilometers per degree of longitude difference;- where
 and
and  are the meridional and its perpendicular, or "normal", radii of curvature (the expressions in the FCC formula are derived from the binomial seriesBinomial seriesIn mathematics, the binomial series is the Taylor series at x = 0 of the function f given by f = α, where is an arbitrary complex number...
are the meridional and its perpendicular, or "normal", radii of curvature (the expressions in the FCC formula are derived from the binomial seriesBinomial seriesIn mathematics, the binomial series is the Taylor series at x = 0 of the function f given by f = α, where is an arbitrary complex number...
expansion form of and
and  , set to the Clarke 1866 reference ellipsoidReference ellipsoidIn geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
, set to the Clarke 1866 reference ellipsoidReference ellipsoidIn geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
).
Polar coordinate flat-Earth formula

- where the colatitude values are in radians. For a latitude measured in degrees, the colatitude in radians may be calculated as follows:

Spherical-surface formulae
If we are willing to accept a possible error of 0.5%, we can use formulas of spherical trigonometry on the sphere that best approximates the surface of the earth.
The shortest distance along the surface of a sphere between two points on the surface is along the great-circle which contains the two points.
Tunnel distance
A tunnel between points on Earth is defined by a line through three-dimensional space between the points of interest. For a spherical Earth, this line is also the chord of the great circle between the points. For points near each other, the tunnel distance is only slightly less than the great-circle distance.
The great circle chord length may be calculated as follows for the corresponding unit sphere:

The tunnel distance between points on the surface of a spherical Earth is:

Great-circle distance
The great-circle distanceGreat-circle distanceThe great-circle distance or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere . Because spherical geometry is rather different from ordinary Euclidean geometry, the equations for distance take on a...
article presents formulae for calculating the exact distance along a great-circle. The great-circle distanceGreat-circle distanceThe great-circle distance or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere . Because spherical geometry is rather different from ordinary Euclidean geometry, the equations for distance take on a...
article includes a worked example for calculating distances by this method.
Ellipsoidal-surface formulae
An ellipsoidal approximation for the surface of the earth may be useful over great distances.
The shortest distance along the surface of an ellipsoid between two points on the surface is along the geodesicGeodesicIn mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
.
Vincenty's formulae
The Vincenty's formulaeVincenty's formulaeVincenty's formulae are two related iterative methods used in geodesy to calculate the distance between two points on the surface of a spheroid, developed by Thaddeus Vincenty They are based on the assumption that the figure of the Earth is an oblate spheroid, and hence are more accurate than...
article presents an algorithm for calculating the geodesic distance between two points on an ellipsoid. The results are accurate to about 0.5 mm; however, the algorithm fails to converge for points that are nearly anti-podalAntipodesIn geography, the antipodes of any place on Earth is the point on the Earth's surface which is diametrically opposite to it. Two points that are antipodal to one another are connected by a straight line running through the centre of the Earth....
. However, the article also gives Vincenty's formulae for the Direct problem (given initial latitude and longitude and the distance and initial direction of a geodesic line, find the lat-lon of the endpoint); those formulae always converge, enabling us to find a near-antipodal geodesic distance by successive approximation.
Bowring's formulae
Vincenty's formulae are intended to maintain accuracy to a millimeter over any distance; if we limit distance to 100–150 km we can get the same accuracy with Bowring's much simpler formulae.
Bowring's formulae appeared in the magazine Surveying and Mapping in 1981. In the linked pdf, "e' 2" is the second eccentricity squared, a constant for the chosen spheroid;
where r is the reciprocal of the flatteningFlatteningThe flattening, ellipticity, or oblateness of an oblate spheroid is a measure of the "squashing" of the spheroid's pole, towards its equator...
(r = 298.257223563 for the WGS84 spheroid). and
and  are the latitudes of the two points,
are the latitudes of the two points,  and
and  are the longitudes;
are the longitudes;  is the difference in latitude (which at one point must be in radians). Calculate A, B, C and w on the first page of the pdf, then skip to "Inverse Problem" on the second page.
is the difference in latitude (which at one point must be in radians). Calculate A, B, C and w on the first page of the pdf, then skip to "Inverse Problem" on the second page.
Lambert's formulae
Lambert's formulae (which appeared in the Journal of the Washington Academy of Sciences in 1942) are also much simpler than Vincenty's and give accuracy on the order of 10 meters over thousands of kilometers. First convert the latitudes ,
,  of the two points to reduced latitudes
of the two points to reduced latitudes  ,
, 

where r is the reciprocal of the flattening (r = 298.257223563 for the WGS84 spheroid).
Then calculate the central angleCentral angleA central angle is an angle which vertex is the center of a circle, and whose sides pass through a pair of points on the circle, thereby subtending an arc between those two points whose angle is equal to the central angle itself...
 in radians between two points
in radians between two points  and
and  on a sphere in the usual wayGreat-circle distanceThe great-circle distance or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere . Because spherical geometry is rather different from ordinary Euclidean geometry, the equations for distance take on a...
on a sphere in the usual wayGreat-circle distanceThe great-circle distance or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere . Because spherical geometry is rather different from ordinary Euclidean geometry, the equations for distance take on a...
(law of cosines or haversine formulaHaversine formulaThe haversine formula is an equation important in navigation, giving great-circle distances between two points on a sphere from their longitudes and latitudes...
), with longitudes and
and  being the same on the sphere as on the spheroid.
being the same on the sphere as on the spheroid.





where is the equatorial radius of the chosen spheroid.
is the equatorial radius of the chosen spheroid.
On the GRS 80GRS 80GRS 80, or Geodetic Reference System 1980, is a geodetic reference system consisting of a global reference ellipsoid and a gravity field model.-Geodesy:...
spheroid Lambert's formula is off by
- 0 North 0 West to 40 North 120 West, 12.6 meters;
- 0N 0W to 40N 60W, 6.6 meters;
- 40N 0W to 40N 60W, 0.85 meter.
See also
- Earth radiusEarth radiusBecause the Earth is not perfectly spherical, no single value serves as its natural radius. Distances from points on the surface to the center range from 6,353 km to 6,384 km...
- Spherical EarthSpherical EarthThe concept of a spherical Earth dates back to ancient Greek philosophy from around the 6th century BC, but remained a matter of philosophical speculation until the 3rd century BC when Hellenistic astronomy established the spherical shape of the earth as a physical given...
- Great-circle distanceGreat-circle distanceThe great-circle distance or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere . Because spherical geometry is rather different from ordinary Euclidean geometry, the equations for distance take on a...
- Vincenty's formulaeVincenty's formulaeVincenty's formulae are two related iterative methods used in geodesy to calculate the distance between two points on the surface of a spheroid, developed by Thaddeus Vincenty They are based on the assumption that the figure of the Earth is an oblate spheroid, and hence are more accurate than...
- Meridian arcMeridian arcIn geodesy, a meridian arc measurement is a highly accurate determination of the distance between two points with the same longitude. Two or more such determinations at different locations then specify the shape of the reference ellipsoid which best approximates the shape of the geoid. This...
External links
- Calculating Geographic Distance: Concepts and Methods
- GeographicLib provides a utility Geod (with source code) for solving direct and inverse geodesic problems. Compared to Vincenty's formulaeVincenty's formulaeVincenty's formulae are two related iterative methods used in geodesy to calculate the distance between two points on the surface of a spheroid, developed by Thaddeus Vincenty They are based on the assumption that the figure of the Earth is an oblate spheroid, and hence are more accurate than...
, this is about 1000 times more accurate (error = 15 nm) and the inverse solution is complete. Here is an online version of Geod.
- It may be interesting to note that: