General set theory
Encyclopedia
General set theory is George Boolos
's (1998) name for a fragment of the axiomatic set theory Z
. GST is sufficient for all mathematics not requiring infinite sets, and is the weakest known set theory whose theorem
s include the Peano axioms
.
ontological
notion, that of set, and a single ontological assumption, namely that all individuals in the universe of discourse (hence all mathematical object
s) are sets. There is a single primitive
binary relation
, set membership; that set a is a member of set b is written a∈b (usually read "a is an element of b").
.
1) Axiom of Extensionality
: The sets x and y are the same set if they have the same members.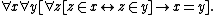
The converse of this axiom follows from the substitution property of equality.
2) Axiom Schema of Specification
(or Separation or Restricted Comprehension): If z is a set and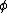
is any property which may be satisfied by all, some, or no elements of z, then there exists a subset y of z containing just those elements x in z which satisfy the property 
. The restriction
to z is necessary to avoid Russell's paradox
and its variants. More formally, let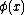
be any formula in the language of GST in which x is free and y is not. Then all instances of the following schema are axioms:
3) Axiom of Adjunction: If x and y are sets, then there exists a set w, the adjunction of x and y, whose members are just y and the members of x.
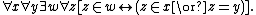
Adjunction refers to an elementary operation on two sets, and has no bearing on the use of that term elsewhere in mathematics, including in category theory.
obtained by omitting the axioms Union
, Power Set
, Infinity
, and Choice, then taking Adjunction, a theorem of Z, as an axiom. The result is a first order theory.
Setting φ(x) in Separation to x≠x, and assuming that the domain is nonempty, assures the existence of the empty set
. Adjunction implies that if x is a set, then so is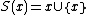
. Given Adjunction, the usual construction of the successor ordinal
s from the empty set
can proceed, one in which the natural number
s are defined as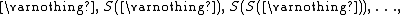
(see Peano's axioms). More generally, given any model M of ZFC, the collection of hereditarily finite set
s in M will satisfy the GST axioms. Therefore, GST cannot prove the existence of even a countable infinite set, that is, of a set whose cardinality is ℵ0. Even if GST did afford a countably infinite set, GST could not prove the existence of a set whose cardinality is ℵ1, that of the continuum, because GST lacks the axiom of power set
. Hence GST cannot ground analysis
and geometry
, and is too weak to serve as a foundation for mathematics.
Boolos was interested in GST only as a fragment of Z
that is just powerful enough to interpret Peano arithmetic. He never lingered over GST, only mentioning it briefly in several papers discussing the systems of Frege's Grundlagen
and Grundgesetze, and how they could be modified to eliminate Russell's paradox
. The system Aξ'[δ0] in Tarski and Givant (1987: 223) is essentially GST with an axiom schema of induction
replacing Specification
, and with the existence of a null set
explicitly assumed.
GST is called STZ in Burgess (2005), p. 223. Burgess's theory ST is GST with Null Set
replacing the axiom schema of specification
. That the letters "ST" also appear in "GST" is a coincidence.
, ST interprets
Robinson arithmetic
(Q), so that ST inherits the nontrivial metamathematics of Q. For example, ST is essentially undecidable
because Q is, and every consistent theory whose theorems include the ST axioms is also essentially undecidable. This includes GST and every axiomatic set theory worth thinking about, assuming these are consistent. In fact, the undecidability
of ST implies the undecidability of first-order logic
with a single binary predicate letter.
Q is also incomplete in the sense of Gödel's incompleteness theorem. Any theory, such as ST and GST, whose theorems include the Q axioms is likewise incomplete. Moreover, the consistency
of GST cannot be proved within GST itself, unless GST is in fact inconsistent.
GST is:
George Boolos
George Stephen Boolos was a philosopher and a mathematical logician who taught at the Massachusetts Institute of Technology.- Life :...
's (1998) name for a fragment of the axiomatic set theory Z
Zermelo set theory
Zermelo set theory, as set out in an important paper in 1908 by Ernst Zermelo, is the ancestor of modern set theory. It bears certain differences from its descendants, which are not always understood, and are frequently misquoted...
. GST is sufficient for all mathematics not requiring infinite sets, and is the weakest known set theory whose theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s include the Peano axioms
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
.
Ontology
The ontology of GST is identical to that of ZFC, and hence is thoroughly canonical. GST features a single primitivePrimitive notion
In mathematics, logic, and formal systems, a primitive notion is an undefined concept. In particular, a primitive notion is not defined in terms of previously defined concepts, but is only motivated informally, usually by an appeal to intuition and everyday experience. In an axiomatic theory or...
ontological
Ontology
Ontology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...
notion, that of set, and a single ontological assumption, namely that all individuals in the universe of discourse (hence all mathematical object
Mathematical object
In mathematics and the philosophy of mathematics, a mathematical object is an abstract object arising in mathematics.Commonly encountered mathematical objects include numbers, permutations, partitions, matrices, sets, functions, and relations...
s) are sets. There is a single primitive
Primitive notion
In mathematics, logic, and formal systems, a primitive notion is an undefined concept. In particular, a primitive notion is not defined in terms of previously defined concepts, but is only motivated informally, usually by an appeal to intuition and everyday experience. In an axiomatic theory or...
binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
, set membership; that set a is a member of set b is written a∈b (usually read "a is an element of b").
Axioms
The symbolic axioms below are from Boolos (1998: 196), and govern how sets behave and interact. The natural language versions of the axioms are intended to aid the intuition. The background logic is first order logic with identityIdentity
-Philosophical topics:* Identity , also called sameness, is whatever makes an entity definable and recognizable* Law of identity, principle of logic stating that an object is the same as itself...
.
1) Axiom of Extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
: The sets x and y are the same set if they have the same members.
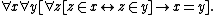
The converse of this axiom follows from the substitution property of equality.
2) Axiom Schema of Specification
Axiom schema of specification
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom schema of specification, axiom schema of separation, subset axiom scheme or axiom schema of restricted comprehension, is a schema of axioms in Zermelo-Fraenkel set theory...
(or Separation or Restricted Comprehension): If z is a set and
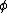is any property which may be satisfied by all, some, or no elements of z, then there exists a subset y of z containing just those elements x in z which satisfy the property . The restrictionRestriction
Restriction may refer to:* Restriction , an aspect of a mathematical function* Restrictions , an album by Cactus* Restriction enzyme, a type of enzyme that cleaves genetic material...
to z is necessary to avoid Russell's paradox
Russell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
and its variants. More formally, let
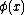be any formula in the language of GST in which x is free and y is not. Then all instances of the following schema are axioms:3) Axiom of Adjunction: If x and y are sets, then there exists a set w, the adjunction of x and y, whose members are just y and the members of x.
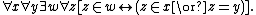
Adjunction refers to an elementary operation on two sets, and has no bearing on the use of that term elsewhere in mathematics, including in category theory.
Discussion
GST is the fragment of ZZermelo set theory
Zermelo set theory, as set out in an important paper in 1908 by Ernst Zermelo, is the ancestor of modern set theory. It bears certain differences from its descendants, which are not always understood, and are frequently misquoted...
obtained by omitting the axioms Union
Axiom of union
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
, Power Set
Axiom of power set
In mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
, Infinity
Axiom of infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
, and Choice, then taking Adjunction, a theorem of Z, as an axiom. The result is a first order theory.
Setting φ(x) in Separation to x≠x, and assuming that the domain is nonempty, assures the existence of the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
. Adjunction implies that if x is a set, then so is
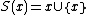. Given Adjunction, the usual construction of the successor ordinalSuccessor ordinal
In set theory, the successor of an ordinal number α is the smallest ordinal number greater than α. An ordinal number that is a successor is called a successor ordinal...
s from the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
can proceed, one in which the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s are defined as
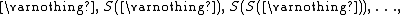(see Peano's axioms). More generally, given any model M of ZFC, the collection of hereditarily finite setHereditarily finite set
In mathematics and set theory, hereditarily finite sets are defined recursively as finite sets consisting of 0 or more hereditarily finite sets.-Formal definition:...
s in M will satisfy the GST axioms. Therefore, GST cannot prove the existence of even a countable infinite set, that is, of a set whose cardinality is ℵ0. Even if GST did afford a countably infinite set, GST could not prove the existence of a set whose cardinality is ℵ1, that of the continuum, because GST lacks the axiom of power set
Axiom of power set
In mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
. Hence GST cannot ground analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, and is too weak to serve as a foundation for mathematics.
Boolos was interested in GST only as a fragment of Z
Zermelo set theory
Zermelo set theory, as set out in an important paper in 1908 by Ernst Zermelo, is the ancestor of modern set theory. It bears certain differences from its descendants, which are not always understood, and are frequently misquoted...
that is just powerful enough to interpret Peano arithmetic. He never lingered over GST, only mentioning it briefly in several papers discussing the systems of Frege's Grundlagen
The Foundations of Arithmetic
Die Grundlagen der Arithmetik is a book by Gottlob Frege, published in 1884, in which he investigates the philosophical foundations of arithmetic. In a tour de force of literary and philosophical merit, Frege demolished other theories of number and developed his own theory of numbers...
and Grundgesetze, and how they could be modified to eliminate Russell's paradox
Russell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
. The system Aξ'[δ0] in Tarski and Givant (1987: 223) is essentially GST with an axiom schema of induction
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
replacing Specification
Axiom schema of specification
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom schema of specification, axiom schema of separation, subset axiom scheme or axiom schema of restricted comprehension, is a schema of axioms in Zermelo-Fraenkel set theory...
, and with the existence of a null set
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
explicitly assumed.
GST is called STZ in Burgess (2005), p. 223. Burgess's theory ST is GST with Null Set
Axiom of empty set
In axiomatic set theory, the axiom of empty set is an axiom of Zermelo–Fraenkel set theory, the fragment thereof Burgess calls ST, and Kripke–Platek set theory.- Formal statement :...
replacing the axiom schema of specification
Axiom schema of specification
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom schema of specification, axiom schema of separation, subset axiom scheme or axiom schema of restricted comprehension, is a schema of axioms in Zermelo-Fraenkel set theory...
. That the letters "ST" also appear in "GST" is a coincidence.
Metamathematics
The most remarkable fact about ST (and hence GST), is that these tiny fragments of set theory give rise to such rich metamathematics. While ST is a small fragment of the well-known canonical set theories ZFC and NBGVon Neumann–Bernays–Gödel set theory
In the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
, ST interprets
Interpretability
In mathematical logic, interpretability is a relation between formal theories that expresses the possibility of interpreting or translating one into the other.-Informal definition:Assume T and S are formal theories...
Robinson arithmetic
Robinson arithmetic
In mathematics, Robinson arithmetic, or Q, is a finitely axiomatized fragment of Peano arithmetic , first set out in R. M. Robinson . Q is essentially PA without the axiom schema of induction. Since Q is weaker than PA, it is incomplete...
(Q), so that ST inherits the nontrivial metamathematics of Q. For example, ST is essentially undecidable
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
because Q is, and every consistent theory whose theorems include the ST axioms is also essentially undecidable. This includes GST and every axiomatic set theory worth thinking about, assuming these are consistent. In fact, the undecidability
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
of ST implies the undecidability of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
with a single binary predicate letter.
Q is also incomplete in the sense of Gödel's incompleteness theorem. Any theory, such as ST and GST, whose theorems include the Q axioms is likewise incomplete. Moreover, the consistency
Consistency
Consistency can refer to:* Consistency , the psychological need to be consistent with prior acts and statements* "Consistency", an 1887 speech by Mark Twain...
of GST cannot be proved within GST itself, unless GST is in fact inconsistent.
GST is:
- Mutually interpretable with Peano arithmetic (thus it has the same proof-theoretic strength as PA);
- Immune to the three great antinomies of naïve set theoryNaive set theoryNaive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
: Russell'sRussell's paradoxIn the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
, Burali-Forti'sBurali-Forti paradoxIn set theory, a field of mathematics, the Burali-Forti paradox demonstrates that naively constructing "the set of all ordinal numbers" leads to a contradiction and therefore shows an antinomy in a system that allows its construction...
, and Cantor'sCantor's paradoxIn set theory, Cantor's paradox is derivable from the theorem that there is no greatest cardinal number, so that the collection of "infinite sizes" is itself infinite...
; - Not finitely axiomatizableAxiom schemaIn mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
. Montague (1961) showed that ZFC is not finitely axiomatizable, and his argument carries over to GST. Hence any axiomatization of GST must either include at least one axiom schemaAxiom schemaIn mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
such as SeparationAxiom schema of specificationIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom schema of specification, axiom schema of separation, subset axiom scheme or axiom schema of restricted comprehension, is a schema of axioms in Zermelo-Fraenkel set theory...
; - Interpretable in relation algebraRelation algebraIn mathematics and abstract algebra, a relation algebra is a residuated Boolean algebra expanded with an involution called converse, a unary operation...
because no part of any GST axiom lies in the scope of more than three quantifiers. This is the necessary and sufficient condition given in Tarski and Givant (1987).
External links
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
: Set Theory -- by Thomas Jech.