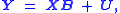General linear model
Encyclopedia
The general linear model (GLM) is a statistical linear model
.
It may be written as
where Y is a matrix with series of multivariate measurements, X is a matrix that might be a design matrix
, B is a matrix containing parameters that are usually to be estimated and U is a matrix containing errors or noise
.
The errors are usually assumed to follow a multivariate normal distribution. If the errors do not follow a multivariate normal distribution, generalized linear models may be used to relax assumptions about Y and U.
The general linear model incorporates a number of different statistical models: ANOVA, ANCOVA
, MANOVA
, MANCOVA
, ordinary linear regression
, t-test and F-test
. If there is only one column in Y (i.e., one dependent variable) then the model can also be referred to as the multiple regression model (multiple linear regression).
Hypothesis tests with the general linear model can be made in two ways: multivariate or as several independent univariate
tests.
In multivariate tests the columns of Y are tested together, whereas in univariate tests the columns of Y are tested independently, i.e., as multiple univariate tests with the same design matrix.
.
Linear model
In statistics, the term linear model is used in different ways according to the context. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However the term is also used in time series analysis with a different...
.
It may be written as
where Y is a matrix with series of multivariate measurements, X is a matrix that might be a design matrix
Design matrix
In statistics, a design matrix is a matrix of explanatory variables, often denoted by X, that is used in certain statistical models, e.g., the general linear model....
, B is a matrix containing parameters that are usually to be estimated and U is a matrix containing errors or noise
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
.
The errors are usually assumed to follow a multivariate normal distribution. If the errors do not follow a multivariate normal distribution, generalized linear models may be used to relax assumptions about Y and U.
The general linear model incorporates a number of different statistical models: ANOVA, ANCOVA
ANCOVA
In statistics, analysis of covariance is a general linear model with a continuous outcome variable and two or more predictor variables where at least one is continuous and at least one is categorical . ANCOVA is a merger of ANOVA and regression for continuous variables...
, MANOVA
MANOVA
Multivariate analysis of variance is a generalized form of univariate analysis of variance . It is used when there are two or more dependent variables. It helps to answer : 1. do changes in the independent variable have significant effects on the dependent variables; 2. what are the interactions...
, MANCOVA
MANCOVA
Multivariate analysis of covariance is an extension of analysis of covariance methods to cover cases where there is more than one dependent variable and where the dependent variables cannot simply be combined....
, ordinary linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
, t-test and F-test
F-test
An F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis.It is most often used when comparing statistical models that have been fit to a data set, in order to identify the model that best fits the population from which the data were sampled. ...
. If there is only one column in Y (i.e., one dependent variable) then the model can also be referred to as the multiple regression model (multiple linear regression).
Hypothesis tests with the general linear model can be made in two ways: multivariate or as several independent univariate
Univariate
In mathematics, univariate refers to an expression, equation, function or polynomial of only one variable. Objects of any of these types but involving more than one variable may be called multivariate...
tests.
In multivariate tests the columns of Y are tested together, whereas in univariate tests the columns of Y are tested independently, i.e., as multiple univariate tests with the same design matrix.
Applications
An application of the general linear model appears in the analysis of multiple brain scans in scientific experiments where Y contains data from brain scanners, X contains experimental design variables and confounds. It is usually tested in a univariate way (usually referred to a mass-univariate in this setting) and is often referred to as statistical parametric mappingStatistical parametric mapping
Statistical parametric mapping or SPM is a statistical technique created by Karl Friston for examining differences in brain activity recorded during functional neuroimaging experiments using neuroimaging technologies such as fMRI or PET...
.