
Gauge anomaly
Encyclopedia
In theoretical physics
, a gauge anomaly is an example of an anomaly
: it is an effect of quantum mechanics
—usually a one-loop diagram—that invalidates the gauge symmetry of a quantum field theory
; i.e. of a gauge theory
.
Anomalies in gauge symmetries lead to an inconsistency, since a gauge symmetry is required in order to cancel unphysical degrees of freedom with a negative norm (such as a photon
polarized in the time direction). Therefore all gauge anomalies must cancel out. This indeed happens in the Standard Model
.
The term gauge anomaly is usually used for vector gauge anomalies. Another type of gauge anomaly is the gravitational anomaly
, because reparametrization is a gauge symmetry in gravitation
.
is a vector), the anomaly is a chiral anomaly
, and can be calculated exactly at one loop level, via a Feynman diagram
with a chiral
fermion
running in the loop (a polygon) with n external gauge boson
s attached to the loop where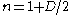 where
where 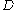 is the spacetime
is the spacetime
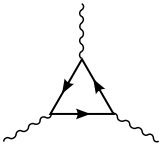
dimension. Anomalies occur only in even spacetime dimensions. For example, the anomalies in the usual 4 spacetime dimensions arise from triangle Feynman diagrams.
Let us look at the (semi)effective action we get after integrating over the chiral fermions. If there is a gauge anomaly, the resulting action will not be gauge invariant. If we denote by the operator corresponding to an infinitesimal gauge transformation by ε, then the Frobenius consistency condition
the operator corresponding to an infinitesimal gauge transformation by ε, then the Frobenius consistency condition
requires that

for any functional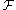 , including the (semi)effective action S where [,] is the Lie bracket
, including the (semi)effective action S where [,] is the Lie bracket
. As is linear in ε, we can write
is linear in ε, we can write

where Ω(4) is d-form
as a functional of the nonintegrated fields and is linear in ε. Let us make the further assumption (which turns out to be valid in all the cases of interest) that this functional is local (i.e. Ω(d)(x) only depends upon the values of the fields and their derivatives at x) and that it can be expressed as the exterior product of p-forms. If the spacetime Md is closed
(i.e. without boundary) and oriented, then it is the boundary of some d+1 dimensional oriented manifold Md+1. If we then arbitrarily extend the fields (including ε) as defined on Md to Md+1 with the only condition being they match on the boundaries and the expression Ω(d), being the exterior product of p-forms, can be extended and defined in the interior, then

The Frobenius consistency condition now becomes

As the previous equation is valid for any arbitrary extension of the fields into the interior,
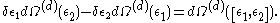
Because of the Frobenius consistency condition, this means that there exists a d+1-form Ωd+1 (not depending upon ε) defined over Md+1 satisfying
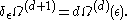
Ωd+1 is often called a Chern-Simons form
.
Once again, if we assume Ωd+1 can be expressed as an exterior product and that it can be extended into a d+1 -form in a d+2 dimensional oriented manifold, we can define
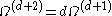
in d+2 dimensions. Ωd+2 is gauge invariant:

as d and δε commute.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, a gauge anomaly is an example of an anomaly
Anomaly (physics)
In quantum physics an anomaly or quantum anomaly is the failure of a symmetry of a theory's classical action to be a symmetry of any regularization of the full quantum theory. In classical physics an anomaly is the failure of a symmetry to be restored in the limit in which the symmetry-breaking...
: it is an effect of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
—usually a one-loop diagram—that invalidates the gauge symmetry of a quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
; i.e. of a gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
.
Anomalies in gauge symmetries lead to an inconsistency, since a gauge symmetry is required in order to cancel unphysical degrees of freedom with a negative norm (such as a photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
polarized in the time direction). Therefore all gauge anomalies must cancel out. This indeed happens in the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
.
The term gauge anomaly is usually used for vector gauge anomalies. Another type of gauge anomaly is the gravitational anomaly
Gravitational anomaly
In theoretical physics, a gravitational anomaly is an example of a gauge anomaly: it is an effect of quantum mechanics–usually a one-loop diagram—that invalidates the general covariance of a theory of general relativity combined with some other fields. The adjective "gravitational" is derived from...
, because reparametrization is a gauge symmetry in gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
.
Calculation of the anomaly
In vector gauge anomalies (in gauge symmetries whose gauge bosonGauge boson
In particle physics, gauge bosons are bosonic particles that act as carriers of the fundamental forces of nature. More specifically, elementary particles whose interactions are described by gauge theory exert forces on each other by the exchange of gauge bosons, usually as virtual particles.-...
is a vector), the anomaly is a chiral anomaly
Chiral anomaly
A chiral anomaly is the anomalous nonconservation of a chiral current. In some theories of fermions with chiral symmetry, the quantization may lead to the breaking of this chiral symmetry. In that case, the charge associated with the chiral symmetry is not conserved.The non-conservation happens...
, and can be calculated exactly at one loop level, via a Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
with a chiral
Chirality (physics)
A chiral phenomenon is one that is not identical to its mirror image . The spin of a particle may be used to define a handedness for that particle. A symmetry transformation between the two is called parity...
fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
running in the loop (a polygon) with n external gauge boson
Gauge boson
In particle physics, gauge bosons are bosonic particles that act as carriers of the fundamental forces of nature. More specifically, elementary particles whose interactions are described by gauge theory exert forces on each other by the exchange of gauge bosons, usually as virtual particles.-...
s attached to the loop where
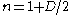 where
where 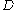 is the spacetime
is the spacetimeSpacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
dimension. Anomalies occur only in even spacetime dimensions. For example, the anomalies in the usual 4 spacetime dimensions arise from triangle Feynman diagrams.

Let us look at the (semi)effective action we get after integrating over the chiral fermions. If there is a gauge anomaly, the resulting action will not be gauge invariant. If we denote by
 the operator corresponding to an infinitesimal gauge transformation by ε, then the Frobenius consistency condition
the operator corresponding to an infinitesimal gauge transformation by ε, then the Frobenius consistency conditionFrobenius theorem (differential topology)
In mathematics, Frobenius' theorem gives necessary and sufficient conditions for finding a maximal set of independent solutions of an overdetermined system of first-order homogeneous linear partial differential equations...
requires that

for any functional
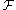 , including the (semi)effective action S where [,] is the Lie bracket
, including the (semi)effective action S where [,] is the Lie bracketLie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
. As
 is linear in ε, we can write
is linear in ε, we can write
where Ω(4) is d-form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
as a functional of the nonintegrated fields and is linear in ε. Let us make the further assumption (which turns out to be valid in all the cases of interest) that this functional is local (i.e. Ω(d)(x) only depends upon the values of the fields and their derivatives at x) and that it can be expressed as the exterior product of p-forms. If the spacetime Md is closed
Closed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
(i.e. without boundary) and oriented, then it is the boundary of some d+1 dimensional oriented manifold Md+1. If we then arbitrarily extend the fields (including ε) as defined on Md to Md+1 with the only condition being they match on the boundaries and the expression Ω(d), being the exterior product of p-forms, can be extended and defined in the interior, then

The Frobenius consistency condition now becomes

As the previous equation is valid for any arbitrary extension of the fields into the interior,
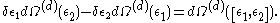
Because of the Frobenius consistency condition, this means that there exists a d+1-form Ωd+1 (not depending upon ε) defined over Md+1 satisfying
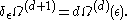
Ωd+1 is often called a Chern-Simons form
Chern-Simons form
In mathematics, the Chern–Simons forms are certain secondary characteristic classes. They have been found to be of interest in gauge theory, and they define the action of Chern–Simons theory...
.
Once again, if we assume Ωd+1 can be expressed as an exterior product and that it can be extended into a d+1 -form in a d+2 dimensional oriented manifold, we can define
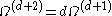
in d+2 dimensions. Ωd+2 is gauge invariant:

as d and δε commute.

