
Finite topological space
Encyclopedia
In mathematics
, a finite topological space is a topological space
for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points.
While topology is mostly interesting only for infinite spaces, finite topological spaces are often used to provide examples of interesting phenomena or counterexample
s to plausible sounding conjectures. William Thurston
has called the study of finite topologies in this sense “an oddball topic that can
lend good insight to a variety of questions.”
s and arbitrary union
s.
Since the power set of a finite set is finite there can be only finitely many open set
s (and only finitely many closed set
s). Therefore one only need check that the union of a finite number of open sets is open. This leads to a simpler description of topologies on a finite set.
Let X be a finite set. A topology on X is a subset τ of P(X) such that
A topology on a finite set is therefore nothing more than a sublattice of (P(X), ⊂) which includes both the bottom element (∅) and the top element (X).
Every finite bounded lattice is complete
since the meet or join of any family of elements can always be reduced to a meet or join of two elements. It follows that in a finite topological space the union or intersection of an arbitrary family of open sets (resp. closed sets) is open (resp. closed).
s on X. Recall that a preorder on X is a binary relation
on X which is reflexive
and transitive
.
Given a (not necessarily finite) topological space X we can define a preorder on X by
where cl{y} denotes the closure
of the singleton set {y}. This preorder is called the specialization preorder on X. Every open set U of X will be an upper set
with respect to ≤ (i.e. if x ∈ U and x ≤ y then y ∈ U). Now if X is finite, the converse is also true: every upper set is open in X. So for finite spaces, the topology on X is uniquely determined by ≤.
Going in the other direction, suppose (X, ≤) is a preordered set. Define a topology τ on X by taking the open sets to be the upper sets with respect to ≤. Then the relation ≤ will be the specialization preorder of (X, τ). The topology defined in this way is called the Alexandrov topology
determined by ≤.
The equivalence between preorders and finite topologies can be interpreted as a version of Birkhoff's representation theorem
, an equivalence between finite distributive lattices (the lattice of open sets of the topology) and partial orders (the partial order of equivalence classes of the preorder). This correspondence also works for a larger class of spaces called finitely generated spaces. Finitely generated spaces can be characterized as the spaces in which an arbitrary intersection of open sets is open. Finite topological spaces are a special class of finitely generated spaces.
∅. The only open set is the empty one. Indeed, this is the only subset of ∅.
Likewise, there is a unique topology on a singleton set {a}. Here the open sets are ∅ and {a}. This topology is both discrete
and trivial
, although in some ways it is better to think of it as a discrete space since it shares more properties with the family of finite discrete spaces.
For any topological space X there is a unique continuous function from ∅ to X, namely the empty function
. There is also a unique continuous function from X to the singleton space {a}, namely the constant function
to a. In the language of category theory
the empty space serves as an initial object
in the category of topological spaces
while the singleton space serves as a terminal object.
The second and third topologies above are easily seen to be homeomorphic. The function from X to itself which swaps a and b is a homeomorphism. A topological space homeomorphic to one of these is called a Sierpiński space
. So, in fact, there are only three inequivalent topologies on a two point set: the trivial one, the discrete one, and the Sierpiński topology.
The specialization preorder on the Sierpiński space {a,b} with {b} open is given by: a ≤ a, b ≤ b, and a ≤ b.
The last 5 of these are all T0. The first one is trivial, while in 2, 3, and 4 the points a and b are topologically indistinguishable.
since any open cover must already be finite. Indeed, compact spaces are often thought of as a generalization of finite spaces since they share many of the same properties.
Every finite topological space is also second-countable (there are only finitely many open sets) and separable (since the space itself is countable
).
(in particular, if it is Hausdorff
) then it must, in fact, be discrete. This is because the complement
of a point is a finite union of closed points and therefore closed. It follows that each point must be open.
Therefore, any finite topological space which is not discrete cannot be T1, Hausdorff, or anything stronger.
However, it is possible for a non-discrete finite space to be T0. In general, two points x and y are topologically indistinguishable if and only if x ≤ y and y ≤ x, where ≤ is the specialization preorder on X. It follows that a space X is T0 if and only if the specialization preorder ≤ on X is a partial order. There are numerous partial orders on a finite set. Each defines a unique T0 topology.
Similarly, a space is R0 if and only if the specialization preorder is an equivalence relation. Given any equivalence relation on a finite set X the associated topology is the partition topology
on X. The equivalence classes will be the classes of topologically indistinguishable points. Since the partition topology is pseudometrizable, a finite space is R0 if and only if it is completely regular.
Non-discrete finite spaces can also be normal
. The excluded point topology
on any finite set is a completely normal T0 space which is non-discrete.
Γ by taking the points of X as vertices and drawing an edge x → y whenever x ≤ y. The connectivity of a finite space X can be understood by considering the connectivity
of the associated graph Γ.
In any topological space, if x ≤ y then there is a path
from x to y. One can simply take f(0) = x and f(t) = y for t > 0. It is easily to verify that f is continuous. It follows that the path components of a finite topological space are precisely the (weakly) connected component
s of the associated graph Γ. That is, there is a topological path from x to y if and only if there is an undirected path
between the corresponding vertices of Γ.
Every finite space is locally path-connected since the set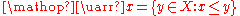
is a path-connected open neighborhood of x that is contained in every other neighborhood. In other words, this single set forms a local base at x.
Therefore, a finite space is connected
if and only if it is path-connected. The connected components are precisely the path components. Each such component is both closed and open
in X.
Finite spaces may have stronger connectivity properties. A finite space X is
For example, the particular point topology
on a finite space is hyperconnected while the excluded point topology
is ultraconnected. The Sierpiński space
is both.
is given by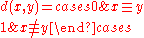
where x ≡ y means x and y are topologically indistinguishable. A finite topological space is metrizable if and only if it is discrete.
Likewise, a topological space is uniformizable
if and only if it is R0. The uniform structure will be the pseudometric uniformity induced by the above pseudometric.
s. A simple example is the pseudocircle, which is space X with four points, two of which are open and two of which are closed. There is a continuous map from the unit circle
S1 to X which is a weak homotopy equivalence (i.e. it induces an isomorphism
of homotopy group
s). It follows that the fundamental group of the pseudocircle is infinite cyclic.
More generally it has been shown that for any finite abstract simplicial complex
K, there is a finite topological space XK and a weak homotopy equivalence f : |K| → XK where |K| is the geometric realization of K. It follows that the homotopy groups of |K| and XK are isomorphic.
s on the set, and T0 topologies are in one-to-one correspondence with partial orders. Therefore the number of topologies on a finite set is equal to the number of preorders and the number of T0 topologies is equal to the number of partial orders.
The table below lists the number of distinct (T0) topologies on a set with n elements. It also lists the number of inequivalent (i.e. nonhomeomorphic) topologies.
Let T(n) denote the number of distinct topologies on a set with n points. There is no known simple formula to compute T(n) for arbitrary n. The Online Encyclopedia of Integer Sequences presently lists T(n) for n ≤ 18.
The number of distinct T0 topologies on a set with n points, denoted T0(n), is related to T(n) by the formula
where S(n,k) denotes the Stirling number of the second kind.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a finite topological space is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points.
While topology is mostly interesting only for infinite spaces, finite topological spaces are often used to provide examples of interesting phenomena or counterexample
Counterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
s to plausible sounding conjectures. William Thurston
William Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
has called the study of finite topologies in this sense “an oddball topic that can
lend good insight to a variety of questions.”
As a bounded sublattice
A topology on a set X is defined as a subset of P(X), the power set of X, which includes both ∅ and X and is closed under finite intersectionIntersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
s and arbitrary union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
s.
Since the power set of a finite set is finite there can be only finitely many open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s (and only finitely many closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s). Therefore one only need check that the union of a finite number of open sets is open. This leads to a simpler description of topologies on a finite set.
Let X be a finite set. A topology on X is a subset τ of P(X) such that
- ∅ ∈ τ and X ∈ τ
- if U and V are in τ then U ∪ V ∈ τ
- if U and V are in τ then U ∩ V ∈ τ
A topology on a finite set is therefore nothing more than a sublattice of (P(X), ⊂) which includes both the bottom element (∅) and the top element (X).
Every finite bounded lattice is complete
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
since the meet or join of any family of elements can always be reduced to a meet or join of two elements. It follows that in a finite topological space the union or intersection of an arbitrary family of open sets (resp. closed sets) is open (resp. closed).
Specialization preorder
Topologies on a finite set X are in one-to-one correspondence with preorderPreorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
s on X. Recall that a preorder on X is a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
on X which is reflexive
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
and transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
.
Given a (not necessarily finite) topological space X we can define a preorder on X by
- x ≤ y if and only if x ∈ cl{y}
where cl{y} denotes the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of the singleton set {y}. This preorder is called the specialization preorder on X. Every open set U of X will be an upper set
Upper set
In mathematics, an upper set of a partially ordered set is a subset U with the property that x is in U and x≤y imply y is in U....
with respect to ≤ (i.e. if x ∈ U and x ≤ y then y ∈ U). Now if X is finite, the converse is also true: every upper set is open in X. So for finite spaces, the topology on X is uniquely determined by ≤.
Going in the other direction, suppose (X, ≤) is a preordered set. Define a topology τ on X by taking the open sets to be the upper sets with respect to ≤. Then the relation ≤ will be the specialization preorder of (X, τ). The topology defined in this way is called the Alexandrov topology
Alexandrov topology
In topology, an Alexandrov space is a topological space in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any finite family of open sets is open...
determined by ≤.
The equivalence between preorders and finite topologies can be interpreted as a version of Birkhoff's representation theorem
Birkhoff's representation theorem
In mathematics, Birkhoff's representation theorem for distributive lattices states that the elements of any finite distributive lattice can be represented as finite sets, in such a way that the lattice operations correspond to unions and intersections of sets...
, an equivalence between finite distributive lattices (the lattice of open sets of the topology) and partial orders (the partial order of equivalence classes of the preorder). This correspondence also works for a larger class of spaces called finitely generated spaces. Finitely generated spaces can be characterized as the spaces in which an arbitrary intersection of open sets is open. Finite topological spaces are a special class of finitely generated spaces.
0 or 1 points
There is a unique topology on the empty setEmpty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
∅. The only open set is the empty one. Indeed, this is the only subset of ∅.
Likewise, there is a unique topology on a singleton set {a}. Here the open sets are ∅ and {a}. This topology is both discrete
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
and trivial
Trivial topology
In topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
, although in some ways it is better to think of it as a discrete space since it shares more properties with the family of finite discrete spaces.
For any topological space X there is a unique continuous function from ∅ to X, namely the empty function
Empty function
In mathematics, an empty function is a function whose domain is the empty set. For each set A, there is exactly one such empty functionf_A: \varnothing \rightarrow A....
. There is also a unique continuous function from X to the singleton space {a}, namely the constant function
Constant function
In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
to a. In the language of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
the empty space serves as an initial object
Initial object
In category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
in the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
while the singleton space serves as a terminal object.
2 points
Let X = {a,b} be a set with 2 elements. There are four distinct topologies on X:- {∅, {a,b}} (the trivial topologyTrivial topologyIn topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
) - {∅, {a}, {a,b}}
- {∅, {b}, {a,b}}
- {∅, {a}, {b}, {a,b}} (the discrete topology)
The second and third topologies above are easily seen to be homeomorphic. The function from X to itself which swaps a and b is a homeomorphism. A topological space homeomorphic to one of these is called a Sierpiński space
Sierpinski space
In mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed.It is the smallest example of a topological space which is neither trivial nor discrete...
. So, in fact, there are only three inequivalent topologies on a two point set: the trivial one, the discrete one, and the Sierpiński topology.
The specialization preorder on the Sierpiński space {a,b} with {b} open is given by: a ≤ a, b ≤ b, and a ≤ b.
3 points
Let X = {a,b,c} be a set with 3 elements. There are 29 distinct topologies on X but only 9 inequivalent topologies:- {∅, {a,b,c}}
- {∅, {c}, {a,b,c}}
- {∅, {a,b}, {a,b,c}}
- {∅, {c}, {a,b}, {a,b,c}}
- {∅, {c}, {b,c}, {a,b,c}}
- {∅, {c}, {a,c}, {b,c}, {a,b,c}}
- {∅, {a}, {b}, {a,b}, {a,b,c}}
- {∅, {b}, {c}, {a,b}, {b,c}, {a,b,c}}
- {∅, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}}
The last 5 of these are all T0. The first one is trivial, while in 2, 3, and 4 the points a and b are topologically indistinguishable.
Compactness and countability
Every finite topological space is compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
since any open cover must already be finite. Indeed, compact spaces are often thought of as a generalization of finite spaces since they share many of the same properties.
Every finite topological space is also second-countable (there are only finitely many open sets) and separable (since the space itself is countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
).
Separation axioms
If a finite topological space is T1T1 space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
(in particular, if it is Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
) then it must, in fact, be discrete. This is because the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of a point is a finite union of closed points and therefore closed. It follows that each point must be open.
Therefore, any finite topological space which is not discrete cannot be T1, Hausdorff, or anything stronger.
However, it is possible for a non-discrete finite space to be T0. In general, two points x and y are topologically indistinguishable if and only if x ≤ y and y ≤ x, where ≤ is the specialization preorder on X. It follows that a space X is T0 if and only if the specialization preorder ≤ on X is a partial order. There are numerous partial orders on a finite set. Each defines a unique T0 topology.
Similarly, a space is R0 if and only if the specialization preorder is an equivalence relation. Given any equivalence relation on a finite set X the associated topology is the partition topology
Partition topology
In mathematics, the partition topology is a topology that can be induced on any set X by partitioning X into disjoint subsets P; these subsets form the basis for the topology...
on X. The equivalence classes will be the classes of topologically indistinguishable points. Since the partition topology is pseudometrizable, a finite space is R0 if and only if it is completely regular.
Non-discrete finite spaces can also be normal
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
. The excluded point topology
Excluded point topology
In mathematics, the excluded point topology is a topology where exclusion of a particular point defines openness. Formally, let X be any set and p ∈ X. The collectionof subsets of X is then the excluded point topology on X....
on any finite set is a completely normal T0 space which is non-discrete.
Connectivity
Connectivity in a finite space X is best understood by considering the specialization preorder ≤ on X. We can associate to any preordered set X a directed graphDirected graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
Γ by taking the points of X as vertices and drawing an edge x → y whenever x ≤ y. The connectivity of a finite space X can be understood by considering the connectivity
Connectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
of the associated graph Γ.
In any topological space, if x ≤ y then there is a path
Path (topology)
In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
from x to y. One can simply take f(0) = x and f(t) = y for t > 0. It is easily to verify that f is continuous. It follows that the path components of a finite topological space are precisely the (weakly) connected component
Connected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
s of the associated graph Γ. That is, there is a topological path from x to y if and only if there is an undirected path
Path (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
between the corresponding vertices of Γ.
Every finite space is locally path-connected since the set
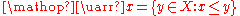
is a path-connected open neighborhood of x that is contained in every other neighborhood. In other words, this single set forms a local base at x.
Therefore, a finite space is connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
if and only if it is path-connected. The connected components are precisely the path components. Each such component is both closed and open
Clopen set
In topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
in X.
Finite spaces may have stronger connectivity properties. A finite space X is
- hyperconnectedHyperconnected spaceIn mathematics, a hyperconnected space is a topological space X that cannot be written as the union of two proper closed sets. The name irreducible space is preferred in algebraic geometry....
if and only if there is a greatest elementGreatest elementIn mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
with respect to the specialization preorder. This is an element whose closure is the whole space X. - ultraconnectedUltraconnected spaceIn mathematics, a topological space X is said to be ultraconnected if no pair of nonempty closed sets of X is disjoint. All ultraconnected spaces are path-connected, normal, limit point compact, and pseudocompact....
if and only if there is a least element with respect to the specialization preorder. This is an element whose only neighborhood is the whole space X.
For example, the particular point topology
Particular point topology
In mathematics, the particular point topology is a topology where sets are considered open if they are empty or contain a particular, arbitrarily chosen, point of the topological space. Formally, let X be any set and p ∈ X. The collectionof subsets of X is then the particular point topology...
on a finite space is hyperconnected while the excluded point topology
Excluded point topology
In mathematics, the excluded point topology is a topology where exclusion of a particular point defines openness. Formally, let X be any set and p ∈ X. The collectionof subsets of X is then the excluded point topology on X....
is ultraconnected. The Sierpiński space
Sierpinski space
In mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed.It is the smallest example of a topological space which is neither trivial nor discrete...
is both.
Additional structure
A finite topological space is pseudometrizable if and only if it is R0. In this case, one possible pseudometricPseudometric space
In mathematics, a pseudometric space is a generalized metric space in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space, every seminormed space is a pseudometric space...
is given by
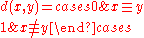
where x ≡ y means x and y are topologically indistinguishable. A finite topological space is metrizable if and only if it is discrete.
Likewise, a topological space is uniformizable
Uniformizable space
In mathematics, a topological space X is uniformizable if there exists a uniform structure on X which induces the topology of X. Equivalently, X is uniformizable if and only if it is homeomorphic to a uniform space .Any metrizable space is uniformizable since the metric uniformity induces the...
if and only if it is R0. The uniform structure will be the pseudometric uniformity induced by the above pseudometric.
Algebraic topology
Perhaps surprisingly, there are finite topological spaces with nontrivial fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
s. A simple example is the pseudocircle, which is space X with four points, two of which are open and two of which are closed. There is a continuous map from the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
S1 to X which is a weak homotopy equivalence (i.e. it induces an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
of homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s). It follows that the fundamental group of the pseudocircle is infinite cyclic.
More generally it has been shown that for any finite abstract simplicial complex
Abstract simplicial complex
In mathematics, an abstract simplicial complex is a purely combinatorial description of the geometric notion of a simplicial complex, consisting of a family of finite sets closed under the operation of taking subsets...
K, there is a finite topological space XK and a weak homotopy equivalence f : |K| → XK where |K| is the geometric realization of K. It follows that the homotopy groups of |K| and XK are isomorphic.
Number of topologies on a finite set
As discussed above, topologies on a finite set are in one-to-one correspondence with preorderPreorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
s on the set, and T0 topologies are in one-to-one correspondence with partial orders. Therefore the number of topologies on a finite set is equal to the number of preorders and the number of T0 topologies is equal to the number of partial orders.
The table below lists the number of distinct (T0) topologies on a set with n elements. It also lists the number of inequivalent (i.e. nonhomeomorphic) topologies.
| n | Distinct topologies | Distinct T0 topologies | Inequivalent topologies | Inequivalent T0 topologies |
|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 3 | 3 | 2 |
| 3 | 29 | 19 | 9 | 5 |
| 4 | 355 | 219 | 33 | 16 |
| 5 | 6942 | 4231 | 139 | 63 |
| 6 | 209527 | 130023 | 718 | 318 |
| 7 | 9535241 | 6129859 | 4535 | 2045 |
| 8 | 642779354 | 431723379 | 35979 | 16999 |
| 9 | 63260289423 | 44511042511 | 363083 | 183231 |
| 10 | 8977053873043 | 6611065248783 | 4717687 | 2567284 |
| OEIS | A000798 | A001035 | A001930 | A000112 |
Let T(n) denote the number of distinct topologies on a set with n points. There is no known simple formula to compute T(n) for arbitrary n. The Online Encyclopedia of Integer Sequences presently lists T(n) for n ≤ 18.
The number of distinct T0 topologies on a set with n points, denoted T0(n), is related to T(n) by the formula

where S(n,k) denotes the Stirling number of the second kind.

