
Finite potential well
Encyclopedia
The finite potential well (also known as the finite square well) is a concept from quantum mechanics
. It is an extension of the infinite potential well, in which a particle is confined to a box, but one which has finite potential
walls. Unlike the infinite potential well, there is a probability
associated with the particle being found outside the box. The quantum mechanical interpretation is unlike the classical interpretation, where if the total energy
of the particle is less than potential energy barrier of the walls it cannot be found outside the box. In the quantum interpretation, there is a non-zero probability of the particle being outside the box even when the energy of the particle is less than the potential energy barrier of the walls (cf quantum tunnelling
).

where
 ,
, is Planck's constant,
is Planck's constant, is the mass
is the mass
of the particle, is the (complex valued) wavefunction
is the (complex valued) wavefunction
that we want to find, is a function describing the potential energy at each point x, and
is a function describing the potential energy at each point x, and is the energy
is the energy
, a real number, sometimes called eigenenergy.
For the case of the particle in a 1-dimensional box of length L, the potential is zero inside the box, but rises abruptly to a value at x = -L/2 and x = L/2. The wavefunction is considered to be made up of different wavefuctions at different ranges of x, depending on whether x is inside or outside of the box. Therefore the wavefunction is defined such that:
at x = -L/2 and x = L/2. The wavefunction is considered to be made up of different wavefuctions at different ranges of x, depending on whether x is inside or outside of the box. Therefore the wavefunction is defined such that:


Letting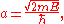
the equation becomes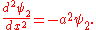
This is a well-studied differential equation
and eigenvalue problem with a general solution of
Hence,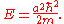
Here, A and B can be any complex number
s, and a can be any real number.
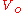 and Equation 1 becomes:
and Equation 1 becomes:

There are two possible families of solutions, depending on whether E is less than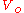 (the particle is bound in the potential) or E is greater than
(the particle is bound in the potential) or E is greater than  (the particle is free).
(the particle is free).
For a free particle, E >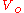 , and letting
, and letting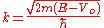
produces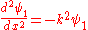
with the same solution form as the inside-well case:

This analysis will first focus on the bound state, where > E. Letting
> E. Letting
produces
where the general solution is exponential: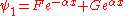
Similarly, for the other region outside the box:

Now in order to find the specific solution for the problem at hand, we must specify the appropriate boundary conditions and find the values for A , B , F , G , H and I that satisfy those conditions.
In this case, the finite potential well is symmetrical, so symmetry can be exploited to reduce the necessary calculations.
Summarizing the previous section:

where we found and
and 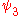 to be:
to be:


We see that as goes to
goes to  , the
, the  term goes to infinity. Likewise, as
term goes to infinity. Likewise, as  goes to
goes to  , the
, the  term goes to infinity. As the wave function must have finite total integral, this means we must set
term goes to infinity. As the wave function must have finite total integral, this means we must set  , and we have:
, and we have:
Next, we know that the overall function must be continuous and differentiable. In other words the values of the functions and their derivatives must match up at the dividing points:
function must be continuous and differentiable. In other words the values of the functions and their derivatives must match up at the dividing points:
These equations have two sorts of solutions, symmetric, for which and
and  , and antisymmetric, for which
, and antisymmetric, for which  and
and  . For the symmetric case we get
. For the symmetric case we get


so taking the ratio gives
 .
.
Similarly for the antisymmetric case we get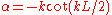 .
.
Recall that both and
and 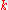 depend on the energy. What we have found is that the continuity conditions cannot be satisfied for an arbitrary value of the energy. Only certain energy values, which are solutions to one or other of these two equations, are allowed. Hence we find, as always, the bound-state energies are quantized.
depend on the energy. What we have found is that the continuity conditions cannot be satisfied for an arbitrary value of the energy. Only certain energy values, which are solutions to one or other of these two equations, are allowed. Hence we find, as always, the bound-state energies are quantized.
The energy equations cannot be solved analytically. Graphical or numerical solutions are aided by rewriting them a little. If we introduce the dimensionless variables and
and  , and note from the definitions of
, and note from the definitions of  and
and 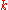 that
that  , where
, where  , the master equations read
, the master equations read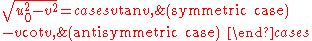
In the plot to the right, for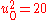 , solutions exist where the blue semicircle intersects the purple or grey curves (
, solutions exist where the blue semicircle intersects the purple or grey curves ( and
and  ). In this case there are exactly three solutions,
). In this case there are exactly three solutions,
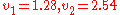 and
and 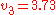 , with the corresponding energies
, with the corresponding energies .
.
If we want, we can go back and find the values of the constants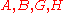 in the equations now (we also need to impose the normalisation condition). On the right we show the energy levels and wave functions in this case (where
in the equations now (we also need to impose the normalisation condition). On the right we show the energy levels and wave functions in this case (where  and
and 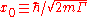 ):
):
We note that however small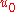 is (however shallow or narrow the well), there is always at least one bound state.
is (however shallow or narrow the well), there is always at least one bound state.
Two special cases are worth noting. As the height of the potential becomes large, , the radius of the semicircle gets larger and the roots get closer and closer to the values
, the radius of the semicircle gets larger and the roots get closer and closer to the values 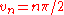 , and we recover the case of the infinite square well.
, and we recover the case of the infinite square well.
The other case is that of a very narrow, deep well - specifically the case and
and  with
with  fixed. As
fixed. As 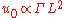 it will tend to zero, and so there will only be one bound state. The approximate solution is then
it will tend to zero, and so there will only be one bound state. The approximate solution is then  , and the energy tends to
, and the energy tends to 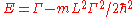 . But this is just the energy of the bound state of a Delta function potential of strength
. But this is just the energy of the bound state of a Delta function potential of strength  , as it should be.
, as it should be.
Note: The above derivation does not consider the possibility that the effective mass of the particle could be different inside the potential well and the region outside the well.
The ground state of a spherically symmetric potential will always have zero orbital angular momentum, and the reduced wave function satisfies the equation
satisfies the equation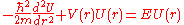
This is identical to the one-dimensional equation, except for the boundary conditions. As before,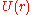 and its first derivative must be continuous at the edge of the well
and its first derivative must be continuous at the edge of the well  . However there is another condition, that
. However there is another condition, that  must be finite, and that requires
must be finite, and that requires 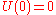 .
.
By comparison with the solutions above, we can see that only the antisymmetric ones have nodes at the origin. Thus only the solutions to are allowed. These correspond to the intersection of the semicircle with the grey curves, and so if the cavity is too shallow or small, there will be no bound state.
are allowed. These correspond to the intersection of the semicircle with the grey curves, and so if the cavity is too shallow or small, there will be no bound state.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. It is an extension of the infinite potential well, in which a particle is confined to a box, but one which has finite potential
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
walls. Unlike the infinite potential well, there is a probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
associated with the particle being found outside the box. The quantum mechanical interpretation is unlike the classical interpretation, where if the total energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of the particle is less than potential energy barrier of the walls it cannot be found outside the box. In the quantum interpretation, there is a non-zero probability of the particle being outside the box even when the energy of the particle is less than the potential energy barrier of the walls (cf quantum tunnelling
Quantum tunnelling
Quantum tunnelling refers to the quantum mechanical phenomenon where a particle tunnels through a barrier that it classically could not surmount. This plays an essential role in several physical phenomena, such as the nuclear fusion that occurs in main sequence stars like the sun, and has important...
).
Particle in a 1-dimensional box
For the 1-dimensional case on the x-axis, the time-independent Schrödinger equation can be written as:
where
 ,
, is Planck's constant,
is Planck's constant, is the mass
is the massMass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of the particle,
 is the (complex valued) wavefunction
is the (complex valued) wavefunctionWavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
that we want to find,
 is a function describing the potential energy at each point x, and
is a function describing the potential energy at each point x, and is the energy
is the energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
, a real number, sometimes called eigenenergy.
For the case of the particle in a 1-dimensional box of length L, the potential is zero inside the box, but rises abruptly to a value
 at x = -L/2 and x = L/2. The wavefunction is considered to be made up of different wavefuctions at different ranges of x, depending on whether x is inside or outside of the box. Therefore the wavefunction is defined such that:
at x = -L/2 and x = L/2. The wavefunction is considered to be made up of different wavefuctions at different ranges of x, depending on whether x is inside or outside of the box. Therefore the wavefunction is defined such that:
Inside the box
For the region inside the box V(x) = 0 and Equation 1 reduces to
Letting
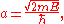
the equation becomes
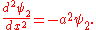
This is a well-studied differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
and eigenvalue problem with a general solution of

Hence,
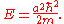
Here, A and B can be any complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, and a can be any real number.
Outside the box
For the region outside of the box, since the potential is constant, V(x) =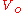 and Equation 1 becomes:
and Equation 1 becomes:
There are two possible families of solutions, depending on whether E is less than
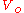 (the particle is bound in the potential) or E is greater than
(the particle is bound in the potential) or E is greater than  (the particle is free).
(the particle is free).For a free particle, E >
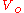 , and letting
, and letting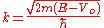
produces
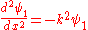
with the same solution form as the inside-well case:

This analysis will first focus on the bound state, where
 > E. Letting
> E. Letting
produces

where the general solution is exponential:
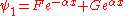
Similarly, for the other region outside the box:

Now in order to find the specific solution for the problem at hand, we must specify the appropriate boundary conditions and find the values for A , B , F , G , H and I that satisfy those conditions.
Finding wavefunctions for the bound state
Solutions to the Schrödinger equation must be continuous, and continuously differentiable. These requirements are boundary conditions on the differential equations previously derived.In this case, the finite potential well is symmetrical, so symmetry can be exploited to reduce the necessary calculations.
Summarizing the previous section:

where we found
 and
and 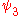 to be:
to be:


We see that as
 goes to
goes to  , the
, the  term goes to infinity. Likewise, as
term goes to infinity. Likewise, as  goes to
goes to  , the
, the  term goes to infinity. As the wave function must have finite total integral, this means we must set
term goes to infinity. As the wave function must have finite total integral, this means we must set  , and we have:
, and we have:  |
and | 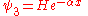 |
Next, we know that the overall
 function must be continuous and differentiable. In other words the values of the functions and their derivatives must match up at the dividing points:
function must be continuous and differentiable. In other words the values of the functions and their derivatives must match up at the dividing points: 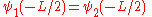 |
 |
|
 |
 |
These equations have two sorts of solutions, symmetric, for which
 and
and  , and antisymmetric, for which
, and antisymmetric, for which  and
and  . For the symmetric case we get
. For the symmetric case we get

so taking the ratio gives
 .
.Similarly for the antisymmetric case we get
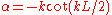 .
.Recall that both
 and
and 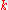 depend on the energy. What we have found is that the continuity conditions cannot be satisfied for an arbitrary value of the energy. Only certain energy values, which are solutions to one or other of these two equations, are allowed. Hence we find, as always, the bound-state energies are quantized.
depend on the energy. What we have found is that the continuity conditions cannot be satisfied for an arbitrary value of the energy. Only certain energy values, which are solutions to one or other of these two equations, are allowed. Hence we find, as always, the bound-state energies are quantized.The energy equations cannot be solved analytically. Graphical or numerical solutions are aided by rewriting them a little. If we introduce the dimensionless variables
 and
and  , and note from the definitions of
, and note from the definitions of  and
and 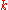 that
that  , where
, where  , the master equations read
, the master equations read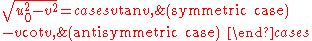
In the plot to the right, for
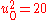 , solutions exist where the blue semicircle intersects the purple or grey curves (
, solutions exist where the blue semicircle intersects the purple or grey curves ( and
and  ). In this case there are exactly three solutions,
). In this case there are exactly three solutions, 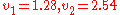 and
and 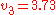 , with the corresponding energies
, with the corresponding energies .
.If we want, we can go back and find the values of the constants
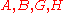 in the equations now (we also need to impose the normalisation condition). On the right we show the energy levels and wave functions in this case (where
in the equations now (we also need to impose the normalisation condition). On the right we show the energy levels and wave functions in this case (where  and
and 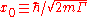 ):
):We note that however small
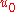 is (however shallow or narrow the well), there is always at least one bound state.
is (however shallow or narrow the well), there is always at least one bound state.Two special cases are worth noting. As the height of the potential becomes large,
 , the radius of the semicircle gets larger and the roots get closer and closer to the values
, the radius of the semicircle gets larger and the roots get closer and closer to the values 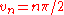 , and we recover the case of the infinite square well.
, and we recover the case of the infinite square well.The other case is that of a very narrow, deep well - specifically the case
 and
and  with
with  fixed. As
fixed. As 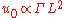 it will tend to zero, and so there will only be one bound state. The approximate solution is then
it will tend to zero, and so there will only be one bound state. The approximate solution is then  , and the energy tends to
, and the energy tends to 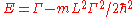 . But this is just the energy of the bound state of a Delta function potential of strength
. But this is just the energy of the bound state of a Delta function potential of strength  , as it should be.
, as it should be.Note: The above derivation does not consider the possibility that the effective mass of the particle could be different inside the potential well and the region outside the well.
Spherical cavity
The results above can be used to show that, contrary to the one-dimensional case, there is not always a bound state in a spherical cavity.The ground state of a spherically symmetric potential will always have zero orbital angular momentum, and the reduced wave function
 satisfies the equation
satisfies the equation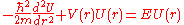
This is identical to the one-dimensional equation, except for the boundary conditions. As before,
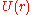 and its first derivative must be continuous at the edge of the well
and its first derivative must be continuous at the edge of the well  . However there is another condition, that
. However there is another condition, that  must be finite, and that requires
must be finite, and that requires 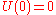 .
.By comparison with the solutions above, we can see that only the antisymmetric ones have nodes at the origin. Thus only the solutions to
 are allowed. These correspond to the intersection of the semicircle with the grey curves, and so if the cavity is too shallow or small, there will be no bound state.
are allowed. These correspond to the intersection of the semicircle with the grey curves, and so if the cavity is too shallow or small, there will be no bound state.See also
- Potential wellPotential wellA potential well is the region surrounding a local minimum of potential energy. Energy captured in a potential well is unable to convert to another type of energy because it is captured in the local minimum of a potential well...
- Delta function potential
- Infinite potential well
- Semicircle potential well
- Quantum tunnellingQuantum tunnellingQuantum tunnelling refers to the quantum mechanical phenomenon where a particle tunnels through a barrier that it classically could not surmount. This plays an essential role in several physical phenomena, such as the nuclear fusion that occurs in main sequence stars like the sun, and has important...

