Finite geometry
Encyclopedia
A finite geometry is any geometric
system that has only a finite number of points
.
Euclidean geometry
, for example, is not finite, because a Euclidean line contains infinitely many points, in fact as many points as there are real numbers
. A finite geometry can have any (finite) number of dimensions.
Finite geometries may be constructed via linear algebra
, as vector space
s over a finite field
, and called Galois geometries
, or can be defined purely combinatorially. Many, but not all, finite geometries are Galois geometries – for example, any finite projective space
of dimension three or greater is isomorphic to a projective space over a finite field (the projectivization of a vector space over a finite field), so in this case there is no distinction, but in dimension two there are combinatorially defined projective planes which are not isomorphic to projective spaces over finite fields, namely the non-Desarguesian plane
s, so in this case there is a distinction.
There are two kinds of finite plane geometry: affine
and projective
.
In an affine geometry
, the normal sense of parallel
lines applies.
In a projective plane
, by contrast, any two lines intersect at a unique point, and so parallel lines do not exist. Both finite affine plane geometry and finite projective plane geometry may be described by fairly simple axiom
s.
An affine plane geometry is a nonempty set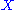
(whose elements are called "points"), along with a nonempty collection 
of subsets of 
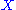(whose elements are called "lines"), such that:
The last axiom ensures that the geometry is not trivial (either empty
or too simple to be of interest, such as a single line with an arbitrary number of points on it), while the first two specify the nature of the geometry.
The simplest affine plane contains only four points; it is called the affine plane of order 2.
Since no three are collinear, any pair of points determines a unique line, and so this plane contains six lines. It corresponds to a tetrahedron where non-intersecting edges are considered "parallel", or a square where not only opposite sides, but also diagonals are considered "parallel".
More generally, a finite affine plane of order
has 
points and 
lines; each line contains 
points, and each point is on 
lines.
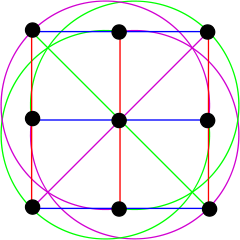A projective plane geometry is a nonempty set 
(whose elements are called "points"), along with a nonempty collection 
of subsets of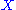 
(whose elements are called "lines"), such that:
An examination of the first two axioms shows that they are nearly identical, except that the roles of points and lines have been interchanged.
This suggests the principle of duality for projective plane geometries, meaning that any true statement valid in all these geometries remains true if we exchange points for lines and lines for points.
The smallest geometry satisfying all three axioms contains seven points. In this simplest of the projective planes, there are also seven lines; each point is on three lines, and each line contains three points.
This particular projective plane is sometimes called the Fano plane
.
If any of the lines is removed from the plane, along with the points on that line, the resulting geometry is the affine plane of order 2.
The Fano plane is called the projective plane of order 2 because it is unique (up to isomorphism).
In general, the projective plane of order n has n2 + n + 1 points and the same number of lines; each line contains n + 1 points, and each point is on n + 1 lines.
A permutation of the Fano plane's seven points that carries collinear
points (points on the same line) to collinear points is called a collineation
of the plane. The full collineation group is of order 168 and is isomorphic to the group PSL(2,7)
= PSL(3,2), and general linear group
GL(3,2).
points (for a projective plane). One major open question in finite geometry is:
This is conjectured to be true, but has not been proven.
Affine and projective planes of order n exist whenever n is a prime power
(a prime number
raised to a positive integer
exponent), by using affine and projective planes over the finite field with
elements. Planes not derived from finite fields also exist, but all known examples have order a prime power.
The best general result to date is the Bruck–Ryser theorem of 1949, which states:
The smallest integer that is not a prime power and not covered by the Bruck–Ryser theorem is 10; 10 is of the form 4k + 2, but it is equal to the sum of squares 12 + 32. The non-existence of a finite plane of order 10 was proven in a computer-assisted proof
that finished in 1989 – see for details.
The next smallest number to consider is 12, for which neither a positive nor a negative result has been proved.
whose points, lines, and planes can be identified with the 1-, 2-, and 3-dimensional subspaces of the 4-dimensional vector space over the field K. There is a set of axioms for projective spaces. The smallest projective space over the field Z2 has 15 points, 35 lines, and 15 planes. Each of the 15 planes contains 7 points and 7 lines. As geometries, they are isomorphic
to the Fano plane
. Every point is contained in 7 lines and every line contains three points. In addition, two distinct points are contained in exactly one line and two planes intersect in exactly one line. In 1892, Gino Fano
was the first to consider such a finite geometry – a three dimensional geometry containing 15 points, 35 lines, and 15 planes, with each plane containing 7 points and 7 lines.
In synthetic projective geometry the undefined elements are taken as points and lines. A plane and a three-space may then be defined using the postulates of incidence and existence:
Postulates of Incidence
P-1: If A and B are distinct points, there is at least one line on both A and B.
P-2: If A and B are distinct points, there is not more than one line on both A and B.
P-3: If A, B, and C are points not all on the same line, and D and E are distinct points such that B, C, and D are on a line and C, A, and E are on a line, there is a point F such that A, B, and F are on a line and also D, E, and F are on a line.
Postulates of Existence
P-4: There exists at least one line.
P-5: There are at least three distinct points on every line.
P-6: Not all points are on the same line.
P-7: Not all points are on the same plane.
P-8: If S3 is a three-space, every point is on S3.
In particular Postulates P-1 through P-8 are satisfied by the points, lines, and planes of the three-space whose points are indicated in Figure 1. This three-space contains exactly 15 points. There are also many very different finite projective three-spaces on which these Postulates are defined.
In general, an n-dimensional projective geometry (n = 4, 5, …) may be obtained by replacing P-8 by postulates stating that:
(i) Not all points are on the same S3, S4, …, Sn-1,
(ii) If Sn is an n-space, every point is on Sn.
The study of these higher-dimensional spaces ( n > 3) has many important applications in advanced mathematical theories.
, which states: “Fifteen schoolgirls walk each day in five groups of three. Arrange the girls’ walk for a week so that in that time, each pair of girls walks together in a group just once.” (See answer in link.) There are 35 different combinations for the girls to walk together. There are also 7 days of the week, and 3 girls in each group. The diagram of this problem provides a visual representation of the Fano space. Diagrams for this problem can be found at http://home.wlu.edu/~mcraea/finite_geometry/Applications/Prob31SchoolGirl/problem31.html
Each color represents the day of the week (seven colors, blue, green, yellow, purple, red, black, and orange). The definition of a Fano space says that each line is on three points. The figure represents this showing that there are 3 points for every line. This is the basis for the answer to the schoolgirl problem. This figure is then rotated 7 times. There are 5 different lines for each day, multiplied by 7 (days) and the result is 35. Then, there are 15 points, and there are also 7 starting lines on each point. This then gives a representation of the Fano space.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
system that has only a finite number of points
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
.
Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, for example, is not finite, because a Euclidean line contains infinitely many points, in fact as many points as there are real numbers
Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
. A finite geometry can have any (finite) number of dimensions.
Finite geometries may be constructed via linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, as vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, and called Galois geometries
Galois geometry
Galois geometry is the branch of finite geometry that is concerned with algebraic and analytic geometry over a finite field . More narrowly, a Galois geometry may be defined as a projective space over a finite field....
, or can be defined purely combinatorially. Many, but not all, finite geometries are Galois geometries – for example, any finite projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
of dimension three or greater is isomorphic to a projective space over a finite field (the projectivization of a vector space over a finite field), so in this case there is no distinction, but in dimension two there are combinatorially defined projective planes which are not isomorphic to projective spaces over finite fields, namely the non-Desarguesian plane
Non-Desarguesian plane
In mathematics, a non-Desarguesian plane, named after Gérard Desargues, is a projective plane that does not satisfy Desargues's theorem, or in other words a plane that is not a Desarguesian plane...
s, so in this case there is a distinction.
Finite planes
The following remarks apply only to finite planes.There are two kinds of finite plane geometry: affine
Affine geometry
In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
and projective
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
.
In an affine geometry
Affine geometry
In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
, the normal sense of parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
lines applies.
In a projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
, by contrast, any two lines intersect at a unique point, and so parallel lines do not exist. Both finite affine plane geometry and finite projective plane geometry may be described by fairly simple axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s.
An affine plane geometry is a nonempty set
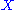(whose elements are called "points"), along with a nonempty collection of subsets of 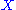(whose elements are called "lines"), such that:
- Given any two distinct points, there is exactly one line that contains both points.
- The parallel postulateParallel postulateIn geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
: Given a line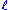
and a point 
not on 
, there exists exactly one line 
containing 
such that 
- There exists a set of four points, no three of which belong to the same line.
The last axiom ensures that the geometry is not trivial (either empty
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
or too simple to be of interest, such as a single line with an arbitrary number of points on it), while the first two specify the nature of the geometry.
Since no three are collinear, any pair of points determines a unique line, and so this plane contains six lines. It corresponds to a tetrahedron where non-intersecting edges are considered "parallel", or a square where not only opposite sides, but also diagonals are considered "parallel".
More generally, a finite affine plane of order
has points and lines; each line contains points, and each point is on lines. (whose elements are called "points"), along with a nonempty collection of subsets of 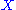(whose elements are called "lines"), such that:
- Given any two distinct points, there is exactly one line that contains both points.
- The intersection of any two distinct lines contains exactly one point.
- There exists a set of four points, no three of which belong to the same line.
An examination of the first two axioms shows that they are nearly identical, except that the roles of points and lines have been interchanged.
This suggests the principle of duality for projective plane geometries, meaning that any true statement valid in all these geometries remains true if we exchange points for lines and lines for points.
The smallest geometry satisfying all three axioms contains seven points. In this simplest of the projective planes, there are also seven lines; each point is on three lines, and each line contains three points.
This particular projective plane is sometimes called the Fano plane
Fano plane
In finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
.
If any of the lines is removed from the plane, along with the points on that line, the resulting geometry is the affine plane of order 2.
The Fano plane is called the projective plane of order 2 because it is unique (up to isomorphism).
In general, the projective plane of order n has n2 + n + 1 points and the same number of lines; each line contains n + 1 points, and each point is on n + 1 lines.
A permutation of the Fano plane's seven points that carries collinear
Incidence (geometry)
In geometry, the relations of incidence are those such as 'lies on' between points and lines , and 'intersects' . That is, they are the binary relations describing how subsets meet...
points (points on the same line) to collinear points is called a collineation
Collineation
In projective geometry, a collineation is a one-to-one and onto map from one projective space to another, or from a projective space to itself, such that the images of collinear points are themselves collinear. All projective linear transformations induce a collineation...
of the plane. The full collineation group is of order 168 and is isomorphic to the group PSL(2,7)
PSL(2,7)
In mathematics, the projective special linear group PSL is a finite simple group that has important applications in algebra, geometry, and number theory. It is the automorphism group of the Klein quartic as well as the symmetry group of the Fano plane...
= PSL(3,2), and general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(3,2).
Order of planes
A finite plane of order n is one such that each line has n points (for an affine plane), or such that each line has points (for a projective plane). One major open question in finite geometry is:
- Is the order of a finite plane always a prime power?
This is conjectured to be true, but has not been proven.
Affine and projective planes of order n exist whenever n is a prime power
Prime power
In mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
(a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
raised to a positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
exponent), by using affine and projective planes over the finite field with
elements. Planes not derived from finite fields also exist, but all known examples have order a prime power.The best general result to date is the Bruck–Ryser theorem of 1949, which states:
- If n is a positive integer of the form 4k + 1 or 4k + 2 and n is not equal to the sum of two integer squares, then n does not occur as the order of a finite plane.
The smallest integer that is not a prime power and not covered by the Bruck–Ryser theorem is 10; 10 is of the form 4k + 2, but it is equal to the sum of squares 12 + 32. The non-existence of a finite plane of order 10 was proven in a computer-assisted proof
Computer-assisted proof
A computer-assisted proof is a mathematical proof that has been at least partially generated by computer.Most computer-aided proofs to date have been implementations of large proofs-by-exhaustion of a mathematical theorem. The idea is to use a computer program to perform lengthy computations, and...
that finished in 1989 – see for details.
The next smallest number to consider is 12, for which neither a positive nor a negative result has been proved.
Finite spaces of 3 or more dimensions
For some important differences between finite plane geometry and the geometry of higher-dimensional finite spaces, see axiomatic projective space. For a discussion of higher-dimensional finite spaces in general, see, for instance, the works of J.W.P. Hirschfeld.Finite three-spaces
Associated with every field K is a (3-dimensional) projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
whose points, lines, and planes can be identified with the 1-, 2-, and 3-dimensional subspaces of the 4-dimensional vector space over the field K. There is a set of axioms for projective spaces. The smallest projective space over the field Z2 has 15 points, 35 lines, and 15 planes. Each of the 15 planes contains 7 points and 7 lines. As geometries, they are isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the Fano plane
Fano plane
In finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
. Every point is contained in 7 lines and every line contains three points. In addition, two distinct points are contained in exactly one line and two planes intersect in exactly one line. In 1892, Gino Fano
Gino Fano
Gino Fano was an Italian mathematician. He was born in Mantua, Italy and died in Verona, Italy.Fano worked on projective and algebraic geometry; the Fano plane, Fano fibration, Fano surface, and Fano varieties are named for him....
was the first to consider such a finite geometry – a three dimensional geometry containing 15 points, 35 lines, and 15 planes, with each plane containing 7 points and 7 lines.
In synthetic projective geometry the undefined elements are taken as points and lines. A plane and a three-space may then be defined using the postulates of incidence and existence:
Postulates of Incidence
P-1: If A and B are distinct points, there is at least one line on both A and B.
P-2: If A and B are distinct points, there is not more than one line on both A and B.
P-3: If A, B, and C are points not all on the same line, and D and E are distinct points such that B, C, and D are on a line and C, A, and E are on a line, there is a point F such that A, B, and F are on a line and also D, E, and F are on a line.
Postulates of Existence
P-4: There exists at least one line.
P-5: There are at least three distinct points on every line.
P-6: Not all points are on the same line.
P-7: Not all points are on the same plane.
P-8: If S3 is a three-space, every point is on S3.
In particular Postulates P-1 through P-8 are satisfied by the points, lines, and planes of the three-space whose points are indicated in Figure 1. This three-space contains exactly 15 points. There are also many very different finite projective three-spaces on which these Postulates are defined.
Finite n-spaces
In general, for any positive integer n, a geometry on an n-space is called an n-dimensional geometry. A four-dimensional projective geometry may be obtained by replacing P-8 by P-8’: Not all points are on the same three-space and by a postulate of closure P-8’’: If S4is a four-space, every point is on S4.In general, an n-dimensional projective geometry (n = 4, 5, …) may be obtained by replacing P-8 by postulates stating that:
(i) Not all points are on the same S3, S4, …, Sn-1,
(ii) If Sn is an n-space, every point is on Sn.
The study of these higher-dimensional spaces ( n > 3) has many important applications in advanced mathematical theories.
Kirkman's Schoolgirl Problem
This 3-space can be modeled by Kirkman's schoolgirl problemKirkman's schoolgirl problem
Kirkman's schoolgirl problem is a problem in combinatorics proposed by Thomas Kirkman in 1850 as Query VI in The Lady's and Gentleman's Diary...
, which states: “Fifteen schoolgirls walk each day in five groups of three. Arrange the girls’ walk for a week so that in that time, each pair of girls walks together in a group just once.” (See answer in link.) There are 35 different combinations for the girls to walk together. There are also 7 days of the week, and 3 girls in each group. The diagram of this problem provides a visual representation of the Fano space. Diagrams for this problem can be found at http://home.wlu.edu/~mcraea/finite_geometry/Applications/Prob31SchoolGirl/problem31.html
Each color represents the day of the week (seven colors, blue, green, yellow, purple, red, black, and orange). The definition of a Fano space says that each line is on three points. The figure represents this showing that there are 3 points for every line. This is the basis for the answer to the schoolgirl problem. This figure is then rotated 7 times. There are 5 different lines for each day, multiplied by 7 (days) and the result is 35. Then, there are 15 points, and there are also 7 starting lines on each point. This then gives a representation of the Fano space.
See also
- Galois geometryGalois geometryGalois geometry is the branch of finite geometry that is concerned with algebraic and analytic geometry over a finite field . More narrowly, a Galois geometry may be defined as a projective space over a finite field....
- Strong Law of Small NumbersStrong Law of Small Numbers"The Strong Law of Small Numbers" is a humorous paper by mathematician Richard K. Guy and also the so-called law that it proclaims: "There aren't enough small numbers to meet the many demands made of them." In other words, any given small number appears in far more contexts than may seem...
– other properties of small finite sets - Linear space
External links
- Essay on Finite Geometry by Michael Greenberg
- Finite geometry (Script)
- Finite Geometry Resources
- J. W. P. Hirschfeld, researcher on finite geometries
- AMS Column: Finite Geometries?
- Galois Geometry and Generalized Polygons, intensive course in 1998