Filter design
Encyclopedia
Filter design is the process of designing a filter
(in the sense in which the term is used in signal processing
, statistics
, and applied mathematics
), often a linear shift-invariant filter, that satisfies a set of requirements, some of which are contradictory. The purpose is to find a realization of the filter that meets each of the requirements to a sufficient degree to make it useful.
The filter design process can be described as an optimization problem where each requirement contributes with a term to an error function which should be minimized. Certain parts of the design process can be automated, but normally an experienced electrical engineer is needed to get a good result.
An important parameter
is the required frequency response
.
In particular, the steepness and complexity of the response curve is a deciding factor for the filter order and feasibility.
A first order recursive
filter will only have a single frequency-dependent component. This means that the slope
of the frequency response is limited to 6 dB
per octave
. For many purposes, this is not sufficient. To achieve steeper slopes, higher order filters are required.
In relation to the desired frequency function, there may also be an accompanying weighting function which describes, for each frequency, how important it is that the resulting frequency function approximates the desired one. The larger weight, the more important is a close approximation.
of the latter. That means that any requirement on the frequency function is a requirement on the impulse response, and vice versa.
However, in certain applications it may be the filter's impulse response that is explicit and the design process then aims at producing as close an approximation as possible to the requested impulse response given all other requirements.
In some cases it may even be relevant to consider a frequency function and impulse response of the filter which are chosen independently from each other. For example, we may want both a specific frequency function of the filter and that the resulting filter have a small effective width in the signal domain as possible. The latter condition can be realized by considering a very narrow function as the wanted impulse response of the filter even though this function has no relation to the desired frequency function. The goal of the design process is then to realize a filter which tries to meet both these contradicting design goals as much as possible.
: the filter response only depends on the current and past inputs. A standard approach is to leave this requirement until the final step. If the resulting filter is not causal, it can be made causal by introducing an appropriate time-shift (or delay). If the filter is a part of a larger system (which it normally is) these types of delays have to be introduced with care since they affect the operation of the entire system.
Filter that do not operate in real time (e.g. for image processing) can be non-causal. This e.g. allows the design of zero delay recursive filter, where the group delay of a causal filter is canceled by its Hermitian non-causal filter.
assures that every limited input signal produces a limited filter response. A filter which does not meet this requirement may in some situations prove useless or even harmful. Certain design approaches can guarantee stability, for example by using only feed-forward circuits such as an FIR filter. On the other hand, filter based on feedback circuits have other advantages and may therefore be preferred, even if this class of filters include unstable filters. In this case, the filters must be carefully designed in order to avoid instability.
According to the uncertainty relation of the Fourier transform, the product of the width of the filter's impulse response function and the width of its frequency function must exceed a certain constant. This means that any requirement on the filter's locality also implies a bound on its frequency function's width. Consequently, it may not be possible to simultaneously meet requirements on the locality of the filter's impulse response function as well as on its frequency function. This is a typical example of contradicting requirements.
There are several ways in which a filter can have different computational complexity. For example, the order of a filter is more or less proportional to the number of operations. This means that by choosing a low order filter, the computation time can be reduced.
For discrete filters the computational complexity is more or less proportional to the number of filter coefficients. If the filter has many coefficients, for example in the case of multidimensional signals such as tomography data, it may be relevant to reduce the number of coefficients by removing those which are sufficiently close to zero. In multirate filters, the number of coefficients by taking advantage of its bandwidth limits, where the input signal is downsampled (e.g. to its critical frequency), and upsampled after filtering.
Another issue related to computational complexity is separability, that is, if and how a filter can be written as a convolution of two or more simpler filters. In particular, this issue is of importance for multidimensional filters, e.g., 2D filter which are used in image processing. In this case, a significant reduction in computational complexity can be obtained if the filter can be separated as the convolution of one 1D filter in the horizontal direction and one 1D filter in the vertical direction. A result of the filter design process may, e.g., be to approximate some desired filter as a separable filter or as a sum of separable filters.
section.
s are classified into one of two basic forms, according to how they respond to a unit impulse:
and beating
with other signals in the system may also be an issue.
effects. Often, this is done by adding analog anti-aliasing
filters at the input and output, thus avoiding any frequency component above the Nyquist frequency
. The complexity (i.e., steepness) of such filters depends on the required signal to noise ratio and the ratio between the sampling rate
and the highest frequency of the signal.
, the product of the width of the frequency function and the width of the impulse response cannot be smaller than a specific constant. This implies that if a specific frequency function is requested, corresponding to a specific frequency width, the minimum width of the filter in the signal domain is set. Vice versa, if the maximum width of the response is given, this determines the smallest possible width in the frequency.
This is a typical example of contradicting requirements where the filter design process may try to find a useful compromise.
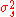be the variance of the input signal and let 
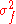be the variance of the filter. The variance of the filter response, 
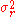, is then given by
This means that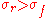
and implies that the localization of various features such as pulses or steps in the filter response is limited by the filter width in the signal domain. If a precise localization is requested, we need a filter of small width in the signal domain and, via the uncertainty principle, its width in the frequency domain cannot be arbitrary small.
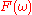be its Fourier transform.
There is a theorem which states that if the first derivative of F which is discontinuous has order
, then f has an asymptotic decay like 
.
A consequence of this theorem is that the frequency function of a filter should be as smooth as possible to allow its impulse response to have a fast decay, and thereby a short width.
, based on the Remez exchange algorithm. Here the user specifies a desired frequency response, a weighting function for errors from this response, and a filter order N. The algorithm then finds the set of N coefficients that minimize the maximum deviation from the ideal. Intuitively, this finds the filter that is as close as you can get to the desired response given that you can use only N coefficients. This method is particularly easy in practice and at least one text includes a program that takes the desired filter and N and returns the optimum coefficients. One possible drawback to filters designed this way is that they contain many small ripples in the passband(s), since such a filter minimizes the peak error.
Another method to finding a discrete FIR filter is filter optimization described in Knutsson et al., which minimizes the integral of the square of the error, instead of its maximum value. In its basic form this approach requires that an ideal frequency function of the filter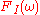
is specified together with a frequency weighting function 
and set of coordinates 
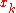in the signal domain where the filter coefficients are located.
An error function
is defined as
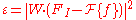
where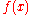
is the discrete filter and 
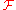is the discrete-time Fourier transform
defined on the specified set of coordinates. The norm used here is, formally, the usual norm on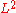
spaces. This means that 
measures the deviation between the requested frequency function of the filter, 
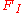, and the actual frequency function of the realized filter, 
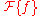. However, the deviation is also subject to the weighting function 
before the error function is computed.
Once the error function is established, the optimal filter is given by the coefficients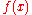
which minimize 
. This can be done by solving the corresponding least squares problem. In practice, the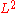 
norm has to be approximated by means of a suitable sum over discrete points in the frequency domain. In general, however, these points should be significantly more than the number of coefficients in the signal domain to obtain a useful approximation.
Filter (signal processing)
In signal processing, a filter is a device or process that removes from a signal some unwanted component or feature. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal...
(in the sense in which the term is used in signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, and applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
), often a linear shift-invariant filter, that satisfies a set of requirements, some of which are contradictory. The purpose is to find a realization of the filter that meets each of the requirements to a sufficient degree to make it useful.
The filter design process can be described as an optimization problem where each requirement contributes with a term to an error function which should be minimized. Certain parts of the design process can be automated, but normally an experienced electrical engineer is needed to get a good result.
Typical design requirements
Typical requirements which are considered in the design process are:- The filter should have a specific frequency responseFrequency responseFrequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...
- The filter should have a specific phase shift or group delayGroup delayGroup delay is a measure of the time delay of the amplitude envelopes of the various sinusoidal components of a signal through a device under test, and is a function of frequency for each component...
- The filter should have a specific impulse responseImpulse responseIn signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
- The filter should be causalCausal filterIn signal processing, a causal filter is a linear and time-invariant causal system. The word causal indicates that the filter output depends only on past and present inputs. A filter whose output also depends on future inputs is non-causal. A filter whose output depends only on future inputs is...
- The filter should be stableBIBO stabilityIn electrical engineering, specifically signal processing and control theory, BIBO stability is a form of stability for linear signals and systems that take inputs. BIBO stands for Bounded-Input Bounded-Output...
- The filter should be localized
- The computational complexity of the filter should be low
- The filter should be implemented in particular hardware or software
The frequency function
Typical examples of frequency function are:- A low-pass filterLow-pass filterA low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
is used to cut unwanted high-frequency signals. - A high-pass filterHigh-pass filterA high-pass filter is a device that passes high frequencies and attenuates frequencies lower than its cutoff frequency. A high-pass filter is usually modeled as a linear time-invariant system...
passes high frequencies fairly well; it is helpful as a filter to cut any unwanted low frequency components. - A band-pass filterBand-pass filterA band-pass filter is a device that passes frequencies within a certain range and rejects frequencies outside that range.Optical band-pass filters are of common usage....
passes a limited range of frequencies. - A band-stop filterBand-stop filterIn signal processing, a band-stop filter or band-rejection filter is a filter that passes most frequencies unaltered, but attenuates those in a specific range to very low levels. It is the opposite of a band-pass filter...
passes frequencies above and below a certain range. A very narrow band-stop filter is known as a notch filter. - A differentiatorDifferentiatorA Differentiator is a circuit that is designed such that the output of the circuit is proportional to the time derivative of the input. There are two types of differentiator circuits, active and passive.-Theory:...
has a amplitude response proportional to the frequency. - A low-shelf filter passes all frequencies, but increases or reduces frequencies below the shelf frequency by specified amount.
- A high-shelf filter passes all frequencies, but increases or reduces frequencies above the shelf frequency by specified amount.
- A peak EQ filter makes a peak or a dip in the frequency response, commonly used in parametric equalizersEqualizationEqualization, is the process of adjusting the balance between frequency components within an electronic signal. The most well known use of equalization is in sound recording and reproduction but there are many other applications in electronics and telecommunications. The circuit or equipment used...
.
An important parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
is the required frequency response
Frequency response
Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...
.
In particular, the steepness and complexity of the response curve is a deciding factor for the filter order and feasibility.
A first order recursive
Infinite impulse response
Infinite impulse response is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time...
filter will only have a single frequency-dependent component. This means that the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of the frequency response is limited to 6 dB
Decibel
The decibel is a logarithmic unit that indicates the ratio of a physical quantity relative to a specified or implied reference level. A ratio in decibels is ten times the logarithm to base 10 of the ratio of two power quantities...
per octave
Octave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
. For many purposes, this is not sufficient. To achieve steeper slopes, higher order filters are required.
In relation to the desired frequency function, there may also be an accompanying weighting function which describes, for each frequency, how important it is that the resulting frequency function approximates the desired one. The larger weight, the more important is a close approximation.
Phase and group delay
- A Hilbert transformHilbert transformIn mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the...
er is a complex band-pass that rejects non-causal signals, and rotates the phase by ±90°. - An all-pass filter passes through all frequencies unchanged, but changes the phase of the signal. This is a filter commonly used in phaser effectsPhaser (effect)A phaser is an audio signal processing technique used to filter a signal by creating a series of peaks and troughs in the frequency spectrum. The position of the peaks and troughs is typically modulated so that they vary over time, creating a sweeping effect...
. Filter of this type can also be used to equalize the group delay of recursive filters. - A fractional delay filter is a low-pass and Lagrange interpolator that has a constant group delay.
The impulse response
There is a direct correspondence between the filter's frequency function and its impulse response: the former is the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the latter. That means that any requirement on the frequency function is a requirement on the impulse response, and vice versa.
However, in certain applications it may be the filter's impulse response that is explicit and the design process then aims at producing as close an approximation as possible to the requested impulse response given all other requirements.
In some cases it may even be relevant to consider a frequency function and impulse response of the filter which are chosen independently from each other. For example, we may want both a specific frequency function of the filter and that the resulting filter have a small effective width in the signal domain as possible. The latter condition can be realized by considering a very narrow function as the wanted impulse response of the filter even though this function has no relation to the desired frequency function. The goal of the design process is then to realize a filter which tries to meet both these contradicting design goals as much as possible.
Causality
In order to be implementable, any time-dependent filter (operating in real time) must be causalCausal filter
In signal processing, a causal filter is a linear and time-invariant causal system. The word causal indicates that the filter output depends only on past and present inputs. A filter whose output also depends on future inputs is non-causal. A filter whose output depends only on future inputs is...
: the filter response only depends on the current and past inputs. A standard approach is to leave this requirement until the final step. If the resulting filter is not causal, it can be made causal by introducing an appropriate time-shift (or delay). If the filter is a part of a larger system (which it normally is) these types of delays have to be introduced with care since they affect the operation of the entire system.
Filter that do not operate in real time (e.g. for image processing) can be non-causal. This e.g. allows the design of zero delay recursive filter, where the group delay of a causal filter is canceled by its Hermitian non-causal filter.
Stability
A stable filterBIBO stability
In electrical engineering, specifically signal processing and control theory, BIBO stability is a form of stability for linear signals and systems that take inputs. BIBO stands for Bounded-Input Bounded-Output...
assures that every limited input signal produces a limited filter response. A filter which does not meet this requirement may in some situations prove useless or even harmful. Certain design approaches can guarantee stability, for example by using only feed-forward circuits such as an FIR filter. On the other hand, filter based on feedback circuits have other advantages and may therefore be preferred, even if this class of filters include unstable filters. In this case, the filters must be carefully designed in order to avoid instability.
Locality
In certain applications we have to deal with signals which contain components which can be described as local phenomena, for example pulses or steps, which have certain time duration. A consequence of applying a filter to a signal is, in intuitive terms, that the duration of the local phenomena is extended by the width of the filter. This implies that it is sometimes important to keep the width of the filter's impulse response function as short as possible.According to the uncertainty relation of the Fourier transform, the product of the width of the filter's impulse response function and the width of its frequency function must exceed a certain constant. This means that any requirement on the filter's locality also implies a bound on its frequency function's width. Consequently, it may not be possible to simultaneously meet requirements on the locality of the filter's impulse response function as well as on its frequency function. This is a typical example of contradicting requirements.
Computational complexity
A general desire in any design is that the number of operations (additions and multiplications) needed to compute the filter response is as low as possible. In certain applications, this desire is a strict requirement, for example due to limited computational resources, limited power resources, or limited time. The last limitation is typical in real-time applications.There are several ways in which a filter can have different computational complexity. For example, the order of a filter is more or less proportional to the number of operations. This means that by choosing a low order filter, the computation time can be reduced.
For discrete filters the computational complexity is more or less proportional to the number of filter coefficients. If the filter has many coefficients, for example in the case of multidimensional signals such as tomography data, it may be relevant to reduce the number of coefficients by removing those which are sufficiently close to zero. In multirate filters, the number of coefficients by taking advantage of its bandwidth limits, where the input signal is downsampled (e.g. to its critical frequency), and upsampled after filtering.
Another issue related to computational complexity is separability, that is, if and how a filter can be written as a convolution of two or more simpler filters. In particular, this issue is of importance for multidimensional filters, e.g., 2D filter which are used in image processing. In this case, a significant reduction in computational complexity can be obtained if the filter can be separated as the convolution of one 1D filter in the horizontal direction and one 1D filter in the vertical direction. A result of the filter design process may, e.g., be to approximate some desired filter as a separable filter or as a sum of separable filters.
Other considerations
It must also be decided how the filter is going to be implemented:- Analog filter
- Analog sampled filterAnalog sampled filterAn analog sampled filter an electronic filter that is a hybrid between an analog and a digital filter. The input signal is analog, and usually stored in capacitors. The time domain is discrete, however. Distinct analog samples are shifted through an array of holding capacitors as in a bucket brigade...
- Digital filterDigital filterIn electronics, computer science and mathematics, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is...
- Mechanical filterMechanical filterA mechanical filter is a signal processing filter usually used in place of an electronic filter at radio frequencies. Its purpose is the same as that of a normal electronic filter: to pass a range of signal frequencies, but to block others. The filter acts on mechanical vibrations which are the...
Analog filters
The design of linear analog filters is for the most part covered in the linear filterLinear filter
Linear filters in the time domain process time-varying input signals to produce output signals, subject to the constraint of linearity.This results from systems composed solely of components classified as having a linear response....
section.
Digital filters
Digital filterDigital filter
In electronics, computer science and mathematics, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is...
s are classified into one of two basic forms, according to how they respond to a unit impulse:
- Finite impulse responseFinite impulse responseA finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
, or FIR, filters express each output sample as a weighted sum of the last N inputs, where N is the order of the filter. Since they do not use feedback, they are inherently stable. If the coefficients are symmetrical (the usual case), then such a filter is linear phaseLinear phaseLinear phase is a property of a filter, where the phase response of the filter is a linear function of frequency, excluding the possibility of wraps at \pm\pi. In a causal system, perfect linear phase can be achieved with a discrete-time FIR filter...
, so it delaysGroup delayGroup delay is a measure of the time delay of the amplitude envelopes of the various sinusoidal components of a signal through a device under test, and is a function of frequency for each component...
signals of all frequencies equally. This is important in many applications. It is also straightforward to avoid overflow in an FIR filter. The main disadvantage is that they may require significantly more processingProcess (computing)In computing, a process is an instance of a computer program that is being executed. It contains the program code and its current activity. Depending on the operating system , a process may be made up of multiple threads of execution that execute instructions concurrently.A computer program is a...
and memoryComputer storageComputer data storage, often called storage or memory, refers to computer components and recording media that retain digital data. Data storage is one of the core functions and fundamental components of computers....
resources than cleverly designed IIR variants. FIR filters are generally easier to design than IIR filters - the Parks-McClellan filter design algorithmParks-McClellan filter design algorithmThe Parks-McClellan algorithm, published by James McClellan and Thomas Parks in 1972, is an iterative algorithm for finding the optimal Chebyshev finite impulse response filter. The Parks-McClellan algorithm is utilized to design and implement efficient and optimal FIR filters...
(based on the Remez algorithmRemez algorithmThe Remez algorithm , published by Evgeny Yakovlevich Remez in 1934 is an iterative algorithm used to find simple approximations to functions, specifically, approximations by functions in a Chebyshev space that are the best in the uniform norm L∞ sense.A typical...
) is one suitable method for designing quite good filters semi-automatically. (See Methodology.) - Infinite impulse responseInfinite impulse responseInfinite impulse response is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time...
, or IIR, filters are the digital counterpart to analog filters. Such a filter contains internal state, and the output and the next internal state are determined by a linear combinationLinear combinationIn mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the previous inputs and outputs (in other words, they use feedbackFeedbackFeedback describes the situation when output from an event or phenomenon in the past will influence an occurrence or occurrences of the same Feedback describes the situation when output from (or information about the result of) an event or phenomenon in the past will influence an occurrence or...
, which FIR filters normally do not). In theory, the impulse response of such a filter never dies out completely, hence the name IIR, though in practice, this is not true given the finite resolution of computer arithmetic. IIR filters normally require less computingComputingComputing is usually defined as the activity of using and improving computer hardware and software. It is the computer-specific part of information technology...
resources than an FIR filter of similar performance. However, due to the feedback, high order IIR filters may have problems with instabilityInstabilityIn numerous fields of study, the component of instability within a system is generally characterized by some of the outputs or internal states growing without bounds...
, arithmetic overflowArithmetic overflowThe term arithmetic overflow or simply overflow has the following meanings.# In a computer, the condition that occurs when a calculation produces a result that is greater in magnitude than that which a given register or storage location can store or represent.# In a computer, the amount by which a...
, and limit cycles, and require careful design to avoid such pitfalls. Additionally, since the phase shiftPhase (waves)Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
is inherently a non-linear function of frequency, the time delay through such a filter is frequency-dependent, which can be a problem in many situations. 2nd order IIR filters are often called 'biquads' and a common implementation of higher order filters is to cascade biquads. A useful reference for computing biquad coefficients is the RBJ Audio EQ Cookbook.
Sample rate
Unless the sample rate is fixed by some outside constraint, selecting a suitable sample rate is an important design decision. A high rate will require more in terms of computational resources, but less in terms of anti-aliasing filters. InterferenceInterference
In physics, interference is a phenomenon in which two waves superpose to form a resultant wave of greater or lower amplitude. Interference usually refers to the interaction of waves that are correlated or coherent with each other, either because they come from the same source or because they have...
and beating
Beat (acoustics)
In acoustics, a beat is an interference between two sounds of slightly different frequencies, perceived as periodic variations in volume whose rate is the difference between the two frequencies....
with other signals in the system may also be an issue.
Anti-aliasing
For any digital filter design, it is crucial to analyze and avoid aliasingAliasing
In signal processing and related disciplines, aliasing refers to an effect that causes different signals to become indistinguishable when sampled...
effects. Often, this is done by adding analog anti-aliasing
Anti-aliasing
In digital signal processing, spatial anti-aliasing is the technique of minimizing the distortion artifacts known as aliasing when representing a high-resolution image at a lower resolution...
filters at the input and output, thus avoiding any frequency component above the Nyquist frequency
Nyquist frequency
The Nyquist frequency, named after the Swedish-American engineer Harry Nyquist or the Nyquist–Shannon sampling theorem, is half the sampling frequency of a discrete signal processing system...
. The complexity (i.e., steepness) of such filters depends on the required signal to noise ratio and the ratio between the sampling rate
Sampling rate
The sampling rate, sample rate, or sampling frequency defines the number of samples per unit of time taken from a continuous signal to make a discrete signal. For time-domain signals, the unit for sampling rate is hertz , sometimes noted as Sa/s...
and the highest frequency of the signal.
Theoretical basis
Parts of the design problem relate to the fact that certain requirements are described in the frequency domain while others are expressed in the signal domain and that these may contradict. For example, it is not possible to obtain a filter which has both an arbitrary impulse response and arbitrary frequency function. Other effects which refer to relations between the signal and frequency domain are- The uncertainty principle between the signal and frequency domains
- The variance extension theorem
- The asymptotic behaviour of one domain versus discontinuities in the other
The uncertainty principle
As stated in the uncertainty principleUncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
, the product of the width of the frequency function and the width of the impulse response cannot be smaller than a specific constant. This implies that if a specific frequency function is requested, corresponding to a specific frequency width, the minimum width of the filter in the signal domain is set. Vice versa, if the maximum width of the response is given, this determines the smallest possible width in the frequency.
This is a typical example of contradicting requirements where the filter design process may try to find a useful compromise.
The variance extension theorem
Let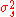 be the variance of the input signal and let 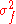be the variance of the filter. The variance of the filter response, 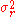, is then given by-
= 
+ 
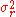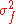
This means that
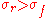and implies that the localization of various features such as pulses or steps in the filter response is limited by the filter width in the signal domain. If a precise localization is requested, we need a filter of small width in the signal domain and, via the uncertainty principle, its width in the frequency domain cannot be arbitrary small.Discontinuities versus asymptotic behaviour
Let f(t) be a function and let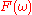 be its Fourier transform.There is a theorem which states that if the first derivative of F which is discontinuous has order
, then f has an asymptotic decay like .A consequence of this theorem is that the frequency function of a filter should be as smooth as possible to allow its impulse response to have a fast decay, and thereby a short width.
Methodology
One common method for designing FIR filters is the Parks-McClellan filter design algorithmParks-McClellan filter design algorithm
The Parks-McClellan algorithm, published by James McClellan and Thomas Parks in 1972, is an iterative algorithm for finding the optimal Chebyshev finite impulse response filter. The Parks-McClellan algorithm is utilized to design and implement efficient and optimal FIR filters...
, based on the Remez exchange algorithm. Here the user specifies a desired frequency response, a weighting function for errors from this response, and a filter order N. The algorithm then finds the set of N coefficients that minimize the maximum deviation from the ideal. Intuitively, this finds the filter that is as close as you can get to the desired response given that you can use only N coefficients. This method is particularly easy in practice and at least one text includes a program that takes the desired filter and N and returns the optimum coefficients. One possible drawback to filters designed this way is that they contain many small ripples in the passband(s), since such a filter minimizes the peak error.
Another method to finding a discrete FIR filter is filter optimization described in Knutsson et al., which minimizes the integral of the square of the error, instead of its maximum value. In its basic form this approach requires that an ideal frequency function of the filter
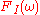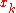is specified together with a frequency weighting function and set of coordinates in the signal domain where the filter coefficients are located.An error function
is defined as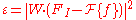where
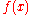is the discrete filter and 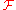is the discrete-time Fourier transformDiscrete-time Fourier transform
In mathematics, the discrete-time Fourier transform is one of the specific forms of Fourier analysis. As such, it transforms one function into another, which is called the frequency domain representation, or simply the "DTFT", of the original function . But the DTFT requires an input function...
defined on the specified set of coordinates. The norm used here is, formally, the usual norm on
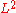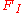spaces. This means that measures the deviation between the requested frequency function of the filter, , and the actual frequency function of the realized filter, 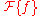. However, the deviation is also subject to the weighting function before the error function is computed.Once the error function is established, the optimal filter is given by the coefficients
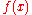which minimize . This can be done by solving the corresponding least squares problem. In practice, the 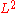norm has to be approximated by means of a suitable sum over discrete points in the frequency domain. In general, however, these points should be significantly more than the number of coefficients in the signal domain to obtain a useful approximation.Simultaneous optimization in both domains
The previous method can be extended to include an additional error term related to a desired filter impulse response in the signal domain, with a corresponding weighting function. The ideal impulse response can be chosen independently of the ideal frequency function and is in practice used to limit the effective width and to remove ringing effects of the resulting filter in the signal domain. This is done by choosing a narrow ideal filter impulse response function, e.g., an impulse, and a weighting function which grows fast with the distance from the origin, e.g., the distance squared. The optimal filter can still be calculated by solving a simple least squares problem and the resulting filter is then a "compromise" which has a total optimal fit to the ideal functions in both domains. An important parameter is the relative strength of the two weighting functions which determines in which domain it is more important to have a good fit relative to the ideal function.External links
- An extensive list of filter design articles and software at Circuit Sage
- A list of digital filter design software at dspGuru
- Analog Filter Design Demystified
- Yehar's digital sound processing tutorial for the braindead! This paper explains simply (between others topics) filters design theory and give some examples