Figure-eight knot (mathematics)
Encyclopedia
In knot theory
, a figure-eight knot (also called Listing's knot) is the unique knot with a crossing number
of four. This is the smallest possible crossing number except for the unknot
and trefoil knot
. The figure-eight knot is a prime knot
.
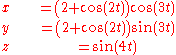
for t varying over the real numbers (see 2D visual realization at bottom right).
The figure-eight knot is prime
, alternating
, rational with an associated value
of 5/2, and is achiral. The figure-eight knot is also a fibered knot
. This follows from other, less simple (but very interesting) representations of the knot:
(1) It is a homogeneous closed braid (namely, the closure of the 3-string braid σ1σ2-1σ1σ2-1), and a theorem of John Stallings shows that any closed homogeneous braid is fibered.
(2) It is the link at (0,0,0,0) of an isolated critical point of a real-polynomial map F: R4→R2, so (according to a theorem of John Milnor
) the Milnor map
of F is actually a fibration. Bernard Perron found the first such F for this knot, namely,
where
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, a figure-eight knot (also called Listing's knot) is the unique knot with a crossing number
Crossing number (knot theory)
In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
of four. This is the smallest possible crossing number except for the unknot
Unknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
and trefoil knot
Trefoil knot
In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
. The figure-eight knot is a prime knot
Prime knot
In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...
.
Origin of name
The name is given because tying a normal figure-eight knot in a rope and then joining the ends together, in the most natural way, gives a model of the mathematical knot.Description
A simple parametric representation of the figure-eight knot is as the set of all points (x,y,z) where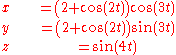
for t varying over the real numbers (see 2D visual realization at bottom right).
The figure-eight knot is prime
Prime knot
In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...
, alternating
Alternating knot
In knot theory, a link diagram is alternating if the crossings alternate under, over, under, over, as you travel along each component of the link. A link is alternating if it has an alternating diagram....
, rational with an associated value
of 5/2, and is achiral. The figure-eight knot is also a fibered knot
Fibered knot
A knot or link Kin the 3-dimensional sphere S^3 is called fibered or fibred if there is a 1-parameter family F_t of Seifert surfaces for K, where the parameter t runs through the points of the unit circle S^1, such that if s is not equal to t...
. This follows from other, less simple (but very interesting) representations of the knot:
(1) It is a homogeneous closed braid (namely, the closure of the 3-string braid σ1σ2-1σ1σ2-1), and a theorem of John Stallings shows that any closed homogeneous braid is fibered.
(2) It is the link at (0,0,0,0) of an isolated critical point of a real-polynomial map F: R4→R2, so (according to a theorem of John Milnor
John Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
) the Milnor map
Milnor map
In mathematics, Milnor maps are named in honor of John Milnor, who introduced them to topology and algebraic geometry in his book Singular Points of Complex Hypersurfaces and earlier lectures. The most studied Milnor maps are actually fibrations, and the phrase Milnor fibration is more commonly...
of F is actually a fibration. Bernard Perron found the first such F for this knot, namely,
where
-
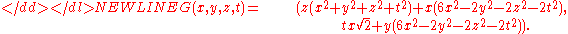
Mathematical properties
The figure-eight knot has played an important role historically (and continues to do so) in the theory of 3-manifold3-manifoldIn mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s. Sometime in the mid-to-late 1970s, William ThurstonWilliam ThurstonWilliam Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
showed that the figure-eight was hyperbolic, by decomposing its complement into two ideal hyperbolic tetrahedra. (Robert Riley and Troels Jørgensen, working independently of each other, had earlier shown that the figure-eight knot was hyperbolic by other means.) This construction, new at the time, led him to many powerful results and methods. For example, he was able to show that all but ten Dehn surgeriesDehn surgeryIn topology, a branch of mathematics, a Dehn surgery, named after Max Dehn, is a specific construction used to modify 3-manifolds. The process takes as input a 3-manifold together with a link...
on the figure-eight knot resulted in non-HakenHaken manifoldIn mathematics, a Haken manifold is a compact, P²-irreducible 3-manifold that is sufficiently large, meaning that it contains a properly embedded two-sided incompressible surface...
, non-Seifert-fiberedSeifert fiber spaceA Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
irreduciblePrime decomposition (3-manifold)In mathematics, the prime decomposition theorem for 3-manifolds states that every compact, orientable 3-manifold is the connected sum of a unique collection of prime 3-manifolds....
3-manifolds; these were the first such examples. Many more have been discovered by generalizing Thurston's construction to other knots and links.
The figure-eight knot is also the hyperbolic knot whose complement has the smallest possible volumeHyperbolic volume (knot)In the mathematical field of knot theory, the hyperbolic volume of a hyperbolic link is simply the volume of the link's complement with respect to its complete hyperbolic metric. The volume is necessarily finite. The hyperbolic volume of a non-hyperbolic knot is often defined to be zero...
, 2.02988... according to the work of Chun Cao and Robert Meyerhoff. From this perspective, the figure-eight knot can be considered the simplest hyperbolic knot. The figure eight knot complement is a double-cover of the Gieseking manifoldGieseking manifoldIn mathematics, the Gieseking manifold, is a cusped hyperbolic 3-manifold of finite volume. It is non-orientable and has the smallest volume among non-compact hyperbolic manifolds, having volume approximately 1.01494161...
, which has the smallest volume among non-compact hyperbolic 3-manifolds.
The figure-eight knot and the (-2, 3, 7) pretzel knot(-2, 3, 7) pretzel knotIn geometric topology, a branch of mathematics, the pretzel knot, sometimes called the Fintushel–Stern knot, is an important example of a pretzel knot which exhibits various interesting phenomena under three-dimensional and four-dimensional surgery constructions.- Mathematical properties :The ...
are the only two hyperbolic knots known to have more than 6 exceptional surgeries, Dehn surgeries resulting in a non-hyperbolic 3-manifold; they have 10 and 7, respectively. A theorem of Lackenby and Meyerhoff, whose proof relies on the geometrization conjectureGeometrization conjectureThurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
and computer assistanceComputer-assisted proofA computer-assisted proof is a mathematical proof that has been at least partially generated by computer.Most computer-aided proofs to date have been implementations of large proofs-by-exhaustion of a mathematical theorem. The idea is to use a computer program to perform lengthy computations, and...
, holds that 10 is the largest possible number of exceptional surgeries of any hyperbolic knot. However, it is not currently known whether the figure-eight knot is the only one that achieves the bound of 10. A well-known conjecture is that the bound (except for the two knots mentioned) is 6.
Invariants
The Alexander polynomialAlexander polynomialIn mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
of the figure-eight knot is
the Conway polynomial is
and the Jones polynomial is
The symmetry between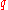 and
and  in the Jones polynomial reflects the fact that the figure-eight knot is achiral.
in the Jones polynomial reflects the fact that the figure-eight knot is achiral.