
Feynman parametrization
Encyclopedia
Feynman parametrization is a technique for evaluating loop integral
s which arise from Feynman diagram
s with one or more loops. However, it is sometimes useful in integration in areas of pure mathematics
as well.
Richard Feynman
observed that:
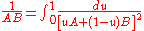
which simplifies evaluating integrals like:
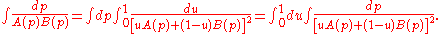
More generally, using the Dirac delta function
:
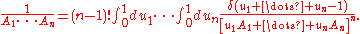
Even more generally, provided that Re(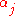 )>0 for all 1 ≤ j ≤ n:
)>0 for all 1 ≤ j ≤ n:
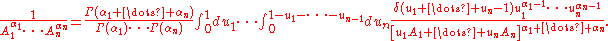
See also Schwinger parametrization.
Loop integral
In quantum field theory and statistical mechanics, loop integrals are the integrals which appear when evaluating the Feynman diagrams with one or more loops by integrating over the internal momenta....
s which arise from Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s with one or more loops. However, it is sometimes useful in integration in areas of pure mathematics
Pure mathematics
Broadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...
as well.
Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
observed that:
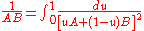
which simplifies evaluating integrals like:
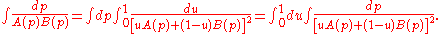
More generally, using the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
:
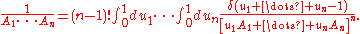
Even more generally, provided that Re(
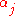 )>0 for all 1 ≤ j ≤ n:
)>0 for all 1 ≤ j ≤ n: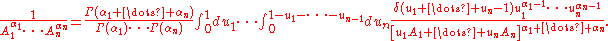
See also Schwinger parametrization.

