
Fermi gas
Encyclopedia
A Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi
, are particles
that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium
, and is characterized by their number density
, temperature
, and the set of available energy states.
By the Pauli principle, no quantum state can be occupied by more than one fermion with identical properties. Thus a Fermi gas, unlike a Bose gas
, is prohibited from condensing into a Bose-Einstein condensate. The total energy of the Fermi gas at absolute zero
is larger than the sum of the single-particle ground state
s because the Pauli principle implies a sort of interaction or pressure that keeps fermions separated and moving. For this reason, the pressure
of a Fermi gas is non-zero even at zero temperature, in contrast to that of a classical ideal gas. This so-called degeneracy pressure stabilizes a neutron star
(a Fermi gas of neutrons) or a white dwarf
star (a Fermi gas of electrons) against the inward pull of gravity, which would ostensibly collapse the star into a Black Hole
. Only when a star is sufficiently massive to overcome the degeneracy pressure can it collapse into a singularity.
It is possible to define a Fermi temperature below which the gas can be considered degenerate (its pressure derives almost exclusively from the Pauli principle). This temperature depends on the mass of the fermions and the density of energy states
. For metals, the electron gas's Fermi temperature is generally many thousands of kelvin
s, so in human applications they can be considered degenerate. The maximum energy of the fermions at zero temperature is called the Fermi energy
. The Fermi energy surface in momentum space is known as the Fermi surface
.
assuming a collection of non-interacting fermions. It is the quantum mechanical
version of an ideal gas
, for the case of fermionic particles. The behavior of electrons in a white dwarf
or neutron
s in a neutron star
can be approximated by treating them as an ideal Fermi gas. Something similar can be done for periodic systems, such as electrons moving in the crystal lattice
of metal
s and semiconductor
s, using the so called quasi-momentum or crystal momentum (Bloch wave
). Since interactions are neglected by definition, the problem of treating the equilibrium properties and dynamics of an ideal Fermi gas reduces to the study of the behavior of single independent particles. As such, it is still relatively tractable and forms the starting point for more advanced theories that deal with interactions, e.g., using the perturbation theory
.
The chemical potential
of the ideal Fermi gas is given by the following expansion (assuming ):
):
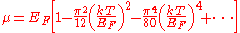
where EF is the Fermi energy
, k is the Boltzmann constant and T is temperature
. Hence, the chemical potential is approximately equal to the Fermi energy at temperatures that are much lower than the characteristic Fermi temperature EF/k. The characteristic temperature is on the order of 105 K
for a metal, hence at room temperature (300 K), the Fermi energy and chemical potential are essentially equivalent. This is significant since it is the chemical potential, not the Fermi energy, which appears in the Fermi-Dirac statistics.
Enrico Fermi
Enrico Fermi was an Italian-born, naturalized American physicist particularly known for his work on the development of the first nuclear reactor, Chicago Pile-1, and for his contributions to the development of quantum theory, nuclear and particle physics, and statistical mechanics...
, are particles
Subatomic particle
In physics or chemistry, subatomic particles are the smaller particles composing nucleons and atoms. There are two types of subatomic particles: elementary particles, which are not made of other particles, and composite particles...
that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium
Thermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
, and is characterized by their number density
Number density
In physics, astronomy, and chemistry, number density is an intensive quantity used to describe the degree of concentration of countable objects in the three-dimensional physical space...
, temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, and the set of available energy states.
By the Pauli principle, no quantum state can be occupied by more than one fermion with identical properties. Thus a Fermi gas, unlike a Bose gas
Bose gas
An ideal Bose gas is a quantum-mechanical version of a classical ideal gas. It is composed of bosons, which have an integer value of spin, and obey Bose–Einstein statistics...
, is prohibited from condensing into a Bose-Einstein condensate. The total energy of the Fermi gas at absolute zero
Absolute zero
Absolute zero is the theoretical temperature at which entropy reaches its minimum value. The laws of thermodynamics state that absolute zero cannot be reached using only thermodynamic means....
is larger than the sum of the single-particle ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
s because the Pauli principle implies a sort of interaction or pressure that keeps fermions separated and moving. For this reason, the pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
of a Fermi gas is non-zero even at zero temperature, in contrast to that of a classical ideal gas. This so-called degeneracy pressure stabilizes a neutron star
Neutron star
A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
(a Fermi gas of neutrons) or a white dwarf
White dwarf
A white dwarf, also called a degenerate dwarf, is a small star composed mostly of electron-degenerate matter. They are very dense; a white dwarf's mass is comparable to that of the Sun and its volume is comparable to that of the Earth. Its faint luminosity comes from the emission of stored...
star (a Fermi gas of electrons) against the inward pull of gravity, which would ostensibly collapse the star into a Black Hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
. Only when a star is sufficiently massive to overcome the degeneracy pressure can it collapse into a singularity.
It is possible to define a Fermi temperature below which the gas can be considered degenerate (its pressure derives almost exclusively from the Pauli principle). This temperature depends on the mass of the fermions and the density of energy states
Density of states
In solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not...
. For metals, the electron gas's Fermi temperature is generally many thousands of kelvin
Kelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
s, so in human applications they can be considered degenerate. The maximum energy of the fermions at zero temperature is called the Fermi energy
Fermi energy
The Fermi energy is a concept in quantum mechanics usually referring to the energy of the highest occupied quantum state in a system of fermions at absolute zero temperature....
. The Fermi energy surface in momentum space is known as the Fermi surface
Fermi surface
In condensed matter physics, the Fermi surface is an abstract boundary useful for predicting the thermal, electrical, magnetic, and optical properties of metals, semimetals, and doped semiconductors. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline...
.
Ideal Fermi gas
An ideal Fermi gas or free Fermi gas is a physical modelMathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
assuming a collection of non-interacting fermions. It is the quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
version of an ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
, for the case of fermionic particles. The behavior of electrons in a white dwarf
White dwarf
A white dwarf, also called a degenerate dwarf, is a small star composed mostly of electron-degenerate matter. They are very dense; a white dwarf's mass is comparable to that of the Sun and its volume is comparable to that of the Earth. Its faint luminosity comes from the emission of stored...
or neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
s in a neutron star
Neutron star
A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
can be approximated by treating them as an ideal Fermi gas. Something similar can be done for periodic systems, such as electrons moving in the crystal lattice
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
of metal
Metal
A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
s and semiconductor
Semiconductor
A semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
s, using the so called quasi-momentum or crystal momentum (Bloch wave
Bloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
). Since interactions are neglected by definition, the problem of treating the equilibrium properties and dynamics of an ideal Fermi gas reduces to the study of the behavior of single independent particles. As such, it is still relatively tractable and forms the starting point for more advanced theories that deal with interactions, e.g., using the perturbation theory
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
.
The chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
of the ideal Fermi gas is given by the following expansion (assuming
 ):
):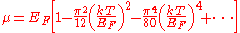
where EF is the Fermi energy
Fermi energy
The Fermi energy is a concept in quantum mechanics usually referring to the energy of the highest occupied quantum state in a system of fermions at absolute zero temperature....
, k is the Boltzmann constant and T is temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
. Hence, the chemical potential is approximately equal to the Fermi energy at temperatures that are much lower than the characteristic Fermi temperature EF/k. The characteristic temperature is on the order of 105 K
Kelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
for a metal, hence at room temperature (300 K), the Fermi energy and chemical potential are essentially equivalent. This is significant since it is the chemical potential, not the Fermi energy, which appears in the Fermi-Dirac statistics.
See also
- Fermi liquidFermi liquidFermi liquid theory is a theoretical model of interacting fermions that describes the normal state of most metals at sufficiently low temperatures. The interaction between the particles of the many-body system does not need to be small...
- Bose gasBose gasAn ideal Bose gas is a quantum-mechanical version of a classical ideal gas. It is composed of bosons, which have an integer value of spin, and obey Bose–Einstein statistics...
- Free electron modelFree electron modelIn solid-state physics, the free electron model is a simple model for the behaviour of valence electrons in a crystal structure of a metallic solid. It was developed principally by Arnold Sommerfeld who combined the classical Drude model with quantum mechanical Fermi-Dirac statistics and hence it...
- Gas in a boxGas in a boxIn quantum mechanics, the results of the quantum particle in a box can be used to look at the equilibrium situation for a quantum ideal gas in a box which is a box containing a large number of molecules which do not interact with each other except for instantaneous thermalizing collisions...

