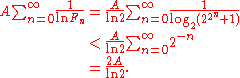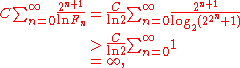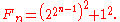Fermat number
Encyclopedia
In mathematics
, a Fermat number, named after Pierre de Fermat
who first studied them, is a positive integer
of the form
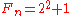
where n is a nonnegative integer. The first few Fermat numbers are:
If 2n + 1 is prime
, and n > 0, it can be shown that n must be a power of two. (If n = ab where 1 ≤ a, b ≤ n and b is odd, then 2n + 1 = (2a)b + 1 ≡ (−1)b + 1 = 0 (mod 2a + 1). See below for complete proof.) In other words, every prime of the form 2n + 1 is a Fermat number, and such primes are called Fermat primes. The only known Fermat primes are F0, F1, F2, F3, and F4.
s:
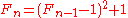
for n ≥ 1,
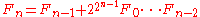


for n ≥ 2. Each of these relations can be proved by mathematical induction
. From the last equation, we can deduce Goldbach's theorem: no two Fermat numbers share a common factor
. To see this, suppose that 0 ≤ i < j and Fi and Fj have a common factor a > 1. Then a divides both
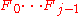
and Fj; hence a divides their difference, 2. Since a > 1, this forces a = 2. This is a contradiction
, because each Fermat number is clearly odd. As a corollary
, we obtain another proof of the infinitude
of the prime numbers: for each Fn, choose a prime factor pn; then the sequence {pn} is an infinite sequence of distinct primes.
Further properties:
 (See floor function
(See floor function
).
d (but admitted he could not prove) that all Fermat numbers are prime. Indeed, the first five Fermat numbers F0,...,F4 are easily shown to be prime. However, this conjecture was refuted by Leonhard Euler
in 1732 when he showed that
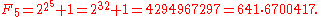
Euler proved that every factor of Fn must have the form k2n+2 + 1.
The fact that 641 is a factor of F5 can be easily deduced from the equalities 641 = 27×5+1 and 641 = 24 + 54. It follows from the first equality that 27×5 ≡ −1 (mod 641) and therefore (raising to the fourth power) that 228×54 ≡ 1 (mod 641). On the other hand, the second equality implies that 54 ≡ −24 (mod 641). These congruences
imply that −232 ≡ 1 (mod 641).
It is widely believed that Fermat was aware of the form of the factors later proved by Euler, so it seems curious why he failed to follow through on the straightforward calculation to find the factor. One common explanation is that Fermat made a computational mistake and was so convinced of the correctness of his claim that he failed to double-check his work.
There are no other known Fermat primes Fn with n > 4. However, little is known about Fermat numbers with large n. In fact, each of the following is an open problem:
it is known that Fn is composite for 5 ≤ n ≤ 32, although complete factorizations of Fn are known only for 0 ≤ n ≤ 11, and there are no known factors for n in {20, 24}. The largest Fermat number known to be composite is F2543548, and its prime factor 9×22543551 + 1 was discovered by Scott Brown in PrimeGrid
's Proth Prime Search on June 22, 2011.
suggests there are only finitely many Fermat primes: according to the prime number theorem
, the "probability
" that a number n is prime is at most A/ln(n), where A is a fixed constant
. Therefore, the total expected number
of Fermat primes is at most
It should be stressed that this argument is in no way a rigorous proof
. For one thing, the argument assumes that Fermat numbers behave "randomly
", yet we have already seen that the factors of Fermat numbers have special properties. If (more sophisticatedly) we regard the conditional probability that n is prime, given that we know all its prime factors exceed B, as at most Aln(B)/ln(n), then using Euler's theorem that the least prime factor of Fn exceeds 2n + 1, we would find instead
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Fermat number, named after Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
who first studied them, is a positive integer
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
of the form
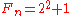
where n is a nonnegative integer. The first few Fermat numbers are:
- 3, 5, 17, 257, 65537, 4294967297, 18446744073709551617, … .
If 2n + 1 is prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, and n > 0, it can be shown that n must be a power of two. (If n = ab where 1 ≤ a, b ≤ n and b is odd, then 2n + 1 = (2a)b + 1 ≡ (−1)b + 1 = 0 (mod 2a + 1). See below for complete proof.) In other words, every prime of the form 2n + 1 is a Fermat number, and such primes are called Fermat primes. The only known Fermat primes are F0, F1, F2, F3, and F4.
Basic properties
The Fermat numbers satisfy the following recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
s:
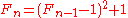
for n ≥ 1,
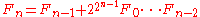


for n ≥ 2. Each of these relations can be proved by mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. From the last equation, we can deduce Goldbach's theorem: no two Fermat numbers share a common factor
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
. To see this, suppose that 0 ≤ i < j and Fi and Fj have a common factor a > 1. Then a divides both
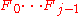
and Fj; hence a divides their difference, 2. Since a > 1, this forces a = 2. This is a contradiction
Contradiction
In classical logic, a contradiction consists of a logical incompatibility between two or more propositions. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other...
, because each Fermat number is clearly odd. As a corollary
Corollary
A corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
, we obtain another proof of the infinitude
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
of the prime numbers: for each Fn, choose a prime factor pn; then the sequence {pn} is an infinite sequence of distinct primes.
Further properties:
- The number of digits D(n,b) of Fn expressed in the baseNumeral systemA numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
b is
 (See floor function
(See floor functionFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
).
- No Fermat number can be expressed as the sum of two primesPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, with the exception of F1 = 2 + 3. - No Fermat prime can be expressed as the difference of two pth powers, where p is an odd prime.
- With the exception of F_{0} and F_{1}, the last digit of a Fermat number is 7.
- The sum of the reciprocals of all the Fermat numbers is irrationalIrrational numberIn mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
. (Solomon W. GolombSolomon W. GolombSolomon Wolf Golomb is an American mathematician and engineer and a professor of electrical engineering at the University of Southern California, best known to the general public and fans of mathematical games as the inventor of polyominoes, the inspiration for the computer game Tetris...
, 1963)
Primality of Fermat numbers
Fermat numbers and Fermat primes were first studied by Pierre de Fermat, who conjectureConjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
d (but admitted he could not prove) that all Fermat numbers are prime. Indeed, the first five Fermat numbers F0,...,F4 are easily shown to be prime. However, this conjecture was refuted by Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
in 1732 when he showed that
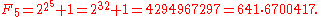
Euler proved that every factor of Fn must have the form k2n+2 + 1.
The fact that 641 is a factor of F5 can be easily deduced from the equalities 641 = 27×5+1 and 641 = 24 + 54. It follows from the first equality that 27×5 ≡ −1 (mod 641) and therefore (raising to the fourth power) that 228×54 ≡ 1 (mod 641). On the other hand, the second equality implies that 54 ≡ −24 (mod 641). These congruences
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
imply that −232 ≡ 1 (mod 641).
It is widely believed that Fermat was aware of the form of the factors later proved by Euler, so it seems curious why he failed to follow through on the straightforward calculation to find the factor. One common explanation is that Fermat made a computational mistake and was so convinced of the correctness of his claim that he failed to double-check his work.
There are no other known Fermat primes Fn with n > 4. However, little is known about Fermat numbers with large n. In fact, each of the following is an open problem:
- Is Fn compositeComposite numberA composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
for all n > 4? - Are there infinitely many Fermat primes? (Eisenstein 1844)
- Are there infinitely many composite Fermat numbers?
it is known that Fn is composite for 5 ≤ n ≤ 32, although complete factorizations of Fn are known only for 0 ≤ n ≤ 11, and there are no known factors for n in {20, 24}. The largest Fermat number known to be composite is F2543548, and its prime factor 9×22543551 + 1 was discovered by Scott Brown in PrimeGrid
PrimeGrid
PrimeGrid is a distributed computing project for searching for prime numbers of world-record size. It makes use of the Berkeley Open Infrastructure for Network Computing platform...
's Proth Prime Search on June 22, 2011.
Heuristic arguments for density
The following heuristic argumentHeuristic argument
A heuristic argument is an argument that reasons from the value of a method or principle that has been shown by experimental investigation to be a useful aid in learning, discovery and problem-solving. A widely-used and important example of a heuristic argument is Occam's Razor....
suggests there are only finitely many Fermat primes: according to the prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
, the "probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
" that a number n is prime is at most A/ln(n), where A is a fixed constant
Constant (mathematics)
In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...
. Therefore, the total expected number
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of Fermat primes is at most
It should be stressed that this argument is in no way a rigorous proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
. For one thing, the argument assumes that Fermat numbers behave "randomly
Randomness
Randomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
", yet we have already seen that the factors of Fermat numbers have special properties. If (more sophisticatedly) we regard the conditional probability that n is prime, given that we know all its prime factors exceed B, as at most Aln(B)/ln(n), then using Euler's theorem that the least prime factor of Fn exceeds 2n + 1, we would find instead
-
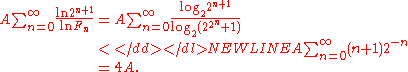
Although such arguments engender the belief that there are only finitely many Fermat primes, one can also produce arguments for the opposite conclusion. Suppose we regard the conditional probability that n is prime, given that we know all its prime factors are 1 modulo M, as at least CM/ln(n). Then using Euler's result that M = 2n + 1 we would find that the expected total number of Fermat primes was at least
and indeed this argument predicts that an asymptotically constant fraction of Fermat numbers are prime!
Equivalent conditions of primality
There are a number of conditions that are equivalentIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
to the primality of Fn.
- Proth's theoremProth's theoremIn number theory, Proth's theorem is a primality test for Proth numbers.It states that if p is a Proth number, of the form k2n + 1 with k odd and k In number theory, Proth's theorem is a primality test for Proth numbers....
(1878) — Let N = k2m + 1 with odd k < 2m. If there is an integer a such that
- then N is prime. Conversely, if the above congruence does not hold, and in addition
-
-
 (See Jacobi symbolJacobi symbolThe Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...
(See Jacobi symbolJacobi symbolThe Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...
)
-
- then N is composite. If N = Fn > 3, then the above Jacobi symbol is always equal to −1 for a = 3, and this special case of Proth's theorem is known as Pépin's testPépin's testIn mathematics, Pépin's test is a primality test, which can be used to determine whether a Fermat number is prime. It is a variant of Proth's test. The test is named for a French mathematician, Théophile Pépin.-Description of the test:...
. Although Pépin's test and Proth's theorem have been implemented on computers to prove the compositeness of many Fermat numbers, neither test gives a specific nontrivial factor. In fact, no specific prime factors are known for n = 20 and 24.- Let n ≥ 3 be a positive odd integer. Then n is a Fermat prime if and only if for every a co-prime to n, a is a primitive rootPrimitive root modulo nIn modular arithmetic, a branch of number theory, a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n...
mod n if and only if a is a quadratic nonresidue mod n. - The Fermat number Fn > 3 is prime if and only if it can be written uniquely as a sum of two nonzero squares, namely
- Let n ≥ 3 be a positive odd integer. Then n is a Fermat prime if and only if for every a co-prime to n, a is a primitive root
- When
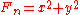 not of the form shown above, a proper factor is:
not of the form shown above, a proper factor is:
- Example 1: F5 = 622642 + 204492, so a proper factor is
- Example 2: F6 = 40468032562 + 14387937592, so a proper factor is
Factorization of Fermat numbers
Because of the size of Fermat numbers, it is difficult to factorize or to prove primality of those. Pépin's testPépin's testIn mathematics, Pépin's test is a primality test, which can be used to determine whether a Fermat number is prime. It is a variant of Proth's test. The test is named for a French mathematician, Théophile Pépin.-Description of the test:...
gives a necessary and sufficient condition for primality of Fermat numbers, and can be implemented by modern computers. The elliptic curve method is a fast method for finding small prime divisors of numbers. Distributed computing project Fermatsearch has successfully found some factors of Fermat numbers. Yves Gallot's proth.exe has been used to find factors of large Fermat numbers. Édouard LucasEdouard LucasFrançois Édouard Anatole Lucas was a French mathematician. Lucas is known for his study of the Fibonacci sequence. The related Lucas sequences and Lucas numbers are named after him.-Biography:...
, improving the above mentioned result by Euler, proved in 1878 that every factor of Fermat number , with n at least 2, is of the form
, with n at least 2, is of the form  (see Proth number), where k is a positive integer; this is in itself almost sufficient to prove the primality of the known Fermat primes.
(see Proth number), where k is a positive integer; this is in itself almost sufficient to prove the primality of the known Fermat primes.
Factorizations of the first ten Fermat numbers are:
F0 = 21 1 = 3 is prime F1 = 22 1 = 5 is prime F2 = 24 1 = 17 is prime F3 = 28 1 = 257 is prime F4 = 216 1 = 65,537 is the largest known Fermat prime F5 = 232 1 = 4,294,967,297 = 641 × 6,700,417 F6 = 264 1 = 18,446,744,073,709,551,617 = 274,177 × 67,280,421,310,721 F7 = 2128 1 = 340,282,366,920,938,463,463,374,607,431,768,211,457 = 59,649,589,127,497,217 × 5,704,689,200,685,129,054,721 F8 = 2256 1 = 115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665,640,564,039,457,584,007,913,129,639,937 = 1,238,926,361,552,897 × 93,461,639,715,357,977,769,163,558,199,606,896,584,051,237,541,638,188,580,280,321 F9 = 2512 1 = 13,407,807,929,942,597,099,574,024,998,205,846,127,479,365,820,592,393,377,723,561,443,721,764,030,073,546,976,801,874,298,166,903,427,690,031,858,186,486,050,853,753,882,811,946,569,946,433,649,006,084,097 = 2,424,833 × 7,455,602,825,647,884,208,337,395,736,200,454,918,783,366,342,657 × 741,640,062,627,530,801,524,787,141,901,937,474,059,940,781,097,519,023,905,821,316,144,415,759,504,705,008,092,818,711,693,940,737 F10 = 21024 1 = 179769313 4862315907 7293051907 8902473361 7976978942 3065727343 0081157732 6758055009 6313270847 7322407536 0211201138 7987139335 7658789768 8144166224 9284743063 9474124377 7678934248 6548527630 2219601246 0941194530 8295208500 5768838150 6823424628 8147391311 0540827237 1633505106 8458629823 9947245938 4797163048 3535632962 4224137217 = 45592577 × 6487031809 × 4659775785 2200185432 6456074307 6778192897 ×
13 0439874405 4881897274 8476879650 9903946608 5308416118 9218689529 5776832416 2514718635 7414022797 7573104895 8987839288 4292384483 1149032913 7987290886 0161794609 4119449010 5959067101 3053190617 1018354491 6096191939 1248853811 6080712299 6723228062 1782075312 7014424577F11 = 22048 1 = 3231700 6071311007 3007148766 8866995196 0444102669 7154840321 3034542752 4655138867 8908931972 0141152291 3463688717 9609218980 1949411955 9150490921 0950881523 8644828312 0630877367 3009960917 5019775038 9652106796 0576383840 6756827679 2218642619 7561618380 9433847617 0470581645 8520363050 4288757589 1541065808 6075523991 2393038552 1914333389 6683424206 8497478656 4569494856 1760353263 2205807780 5659331026 1927084603 1415025859 2864177116 7259436037 1846185735 7598351152 3016459044 0369761323 3287231227 1256847108 2020972515 7101726931 3234696785 4258065669 7935045997 2683529986 3821552516 6389437335 5436021354 3322960464 5318478604 9521481935 5585361105 9596230657 = 319489 × 974849 × 1 6798855634 1760475137 × 35 6084190644 5833920513 ×
1734 6244717914 7555430258 9708643097 7837742184 4723664084 6493470190 6136357919 2879108857 5910383304 0883717798 3810868451 5464219407 1297830613 4189864280 8260145427 5870858924 3873685563 9731189488 6939915854 5506611147 4202161325 5701726056 4139394366 9457932209 6866510895 9685482705 3880726458 2855415193 6401912464 9311825460 9287981573 3057795573 3585049822 7928009094 2872567591 5189121186 2275171431 9229788100 9792510360 3549691727 9912663527 3587832366 4719315477 7091427745 3770382945 8491891759 0325110939 3813224860 4429857397 1650711059 2444621775 4254070691 3047034664 6436034913 8244172330 6598834177
, only F0 to F11 have been completely factoredInteger factorizationIn number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
. The distributed computingDistributed computingDistributed computing is a field of computer science that studies distributed systems. A distributed system consists of multiple autonomous computers that communicate through a computer network. The computers interact with each other in order to achieve a common goal...
project Fermat Search is searching for new factors of Fermat numbers. The set of all Fermat factors is A050922 (or, sorted, A023394) in OEISOn-Line Encyclopedia of Integer SequencesThe On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs...
.
Pseudoprimes and Fermat numbers
Like composite numberComposite numberA composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
s of the form 2p − 1, every composite Fermat number is a strong pseudoprimeStrong pseudoprimeIn number theory, a strong pseudoprime is a composite number that passes a primality test. All primes pass this test, but a small fraction of composites pass as well, making them "false primes"...
to base 2. Because all strong pseudoprimes to base 2 are also Fermat pseudoprimes - i.e.
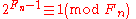
for all Fermat numbers.
Because it is generally believed that all but the first few Fermat numbers are composite, this makes it possible to generate infinitely many strong pseudoprimes to base 2 from the Fermat numbers.
In fact, Rotkiewicz showed in 1964 that the product of any number of prime or composite Fermat numbers will be a Fermat pseudoprime to base 2.
Other theorems about Fermat numbers
Lemma: If n is a positive integer,

proof:

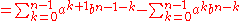

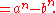
Theorem: If is an odd prime, then
is an odd prime, then  is a power of 2.
is a power of 2.
proof:
If is a positive integer but not a power of 2, then
is a positive integer but not a power of 2, then  where
where
 ,
,  and
and  is odd.
is odd.
By the preceding lemma, for positive integer ,
,

where means "evenly divides". Substituting
means "evenly divides". Substituting 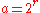 ,
, 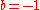 , and
, and  and using that
and using that  is odd,
is odd,

and thus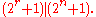
Because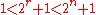 , it follows that
, it follows that  is not prime. Therefore, by contraposition
is not prime. Therefore, by contraposition  must be a power of 2.
must be a power of 2.
Theorem: A Fermat prime cannot be a Wieferich primeWieferich primeIn number theory, a Wieferich prime is a prime number p such that p2 divides 2p − 1 − 1, therefore connecting these primes with Fermat's little theorem, which states that every odd prime p divides 2p − 1 − 1...
.
Proof: We show if is a Fermat prime, then the congruence
is a Fermat prime, then the congruence 
does not satisfy.
It is easy to show
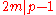 . Now write,
. Now write,  . If the given congruence satisfies, then
. If the given congruence satisfies, then 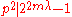 , therefore
, therefore

Hence ,and therefore
,and therefore
 . This leads to
. This leads to
 , which is impossible since
, which is impossible since  .
.
A theorem of Édouard LucasEdouard LucasFrançois Édouard Anatole Lucas was a French mathematician. Lucas is known for his study of the Fibonacci sequence. The related Lucas sequences and Lucas numbers are named after him.-Biography:...
: Any prime divisor p of Fn = is of the form
is of the form  whenever n is greater than one.
whenever n is greater than one.
Sketch of proof:
Let Gp denote the group of non-zero elements of the integers (mod p) under multiplication, which has order p-1. Notice that 2 (strictly speaking, its image (mod p)) has multiplicative order in Gp, so that, by Lagrange's theoremLagrange's theorem (group theory)Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
in Gp, so that, by Lagrange's theoremLagrange's theorem (group theory)Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
, p-1 is divisible by and p has the form
and p has the form  for some integer k,
for some integer k,
as Euler knew. Édouard Lucas went further. Since n is greater than 1, the prime p above is congruent to 1 (mod 8). Hence (as was known to Carl Friedrich GaussCarl Friedrich GaussJohann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
), 2 is a quadratic residue (mod p), that is, there is integer a such that a2 -2 is divisible by p. Then the image of a has order in the group Gp and (using Lagrange's theorem again), p-1 is divisible by
in the group Gp and (using Lagrange's theorem again), p-1 is divisible by 
and p has the form for some integer s.
for some integer s.
In fact, it can be seen directly that 2 is a quadratic residue (mod p), since
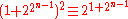 (mod p). Since an
(mod p). Since an
odd power of 2 is a quadratic residue (mod p), so is 2 itself.
Relationship to constructible polygons
An n-sided regular polygon can be constructed with compass and straightedgeCompass and straightedgeCompass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
if and only if n is the product of a power of 2 and distinct Fermat primes. In other words, if and only if n is of the form n = 2kp1p2…ps, where k is a nonnegative integer and the pi are distinct Fermat primes.
A positive integer n is of the above form if and only if its totientEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
φ(n) is a power of 2.
Pseudorandom Number Generation
Fermat primes are particularly useful in generating pseudo-random sequences of numbers in the range 1 … N, where N is a power of 2. The most common method used is to take any seed value between 1 and P − 1, where P is a Fermat prime. Now multiply this by a number A, which is greater than the square root of P and is a primitive rootPrimitive root modulo nIn modular arithmetic, a branch of number theory, a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n...
modulo P (i.e., it is not a quadratic residue). Then take the result modulo P. The result is the new value for the RNG.-
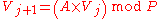 (see Linear congruential generatorLinear congruential generatorA Linear Congruential Generator represents one of the oldest and best-known pseudorandom number generator algorithms. The theory behind them is easy to understand, and they are easily implemented and fast....
(see Linear congruential generatorLinear congruential generatorA Linear Congruential Generator represents one of the oldest and best-known pseudorandom number generator algorithms. The theory behind them is easy to understand, and they are easily implemented and fast....
, RANDU)
This is useful in computer science since most data structures have members with 2X possible values. For example, a byte has 256 (28) possible values (0–255). Therefore to fill a byte or bytes with random values a random number generator which produces values 1–256 can be used, the byte taking the output value − 1. Very large Fermat primes are of particular interest in data encryption for this reason. This method produces only pseudorandom values as, after P − 1 repetitions, the sequence repeats. A poorly chosen multiplier can result in the sequence repeating sooner than P − 1.
Other interesting facts
A Fermat number cannot be a perfect number or part of a pair of amicable numbers.(Luca 2000)
The series of reciprocals of all prime divisors of Fermat numbers is convergent.(Krizek, Luca, Somer 2002)
If nn + 1 is prime, there exists an integer m such that n = 22m. The equation
nn + 1 = F(2m+m)
holds at that time.
Let the largest prime factor of Fermat number Fn be P(Fn). Then,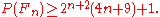 (Grytczuk, Luca and Wojtowicz, 2001)
(Grytczuk, Luca and Wojtowicz, 2001)
Generalized Fermat numbers
Numbers of the form , where a > 1 are called generalized Fermat numbers. By analogy with the ordinary Fermat numbers, it is common to write generalized Fermat numbers of the form
, where a > 1 are called generalized Fermat numbers. By analogy with the ordinary Fermat numbers, it is common to write generalized Fermat numbers of the form  as Fn(a). In this notation, for instance, the number 100,000,001 would be written as F3(10).
as Fn(a). In this notation, for instance, the number 100,000,001 would be written as F3(10).
An odd prime p is a generalized Fermat number if and only if p is congruent to 1 (mod 4) (with the exception of 3 = ).
).
Generalized Fermat primes
Because of the ease of proving their primality, generalized Fermat primes have become in recent years a hot topic for research within the field of number theory. Many of the largest known primes today are generalized Fermat primes.
Generalized Fermat numbers can be prime only for evenEven and odd numbersIn mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2...
a, because if a is odd then every generalized Fermat number will be divisible by 2. By analogy with the heuristic argumentHeuristic argumentA heuristic argument is an argument that reasons from the value of a method or principle that has been shown by experimental investigation to be a useful aid in learning, discovery and problem-solving. A widely-used and important example of a heuristic argument is Occam's Razor....
for the finite number of primes among the base-2 Fermat numbers, it is to be expected that there will be only finitely many generalized Fermat primes for each even base. The smallest prime number Fn(a) with n > 4 is F5(30), or 3032+1.
A more elaborate theory can be used to predict the number of bases for which Fn(a) will be prime for a fixed n. The number of generalized Fermat primes can be roughly expected to halve as n is increased by 1.
See also
- Mersenne primeMersenne primeIn mathematics, a Mersenne number, named after Marin Mersenne , is a positive integer that is one less than a power of two: M_p=2^p-1.\,...
- Pierpont primePierpont primeA Pierpont prime is a prime number of the form2^u 3^v + 1\,for some nonnegative integers u and v. They are named after the mathematician James Pierpont....
- Lucas' theorem
- Proth's theoremProth's theoremIn number theory, Proth's theorem is a primality test for Proth numbers.It states that if p is a Proth number, of the form k2n + 1 with k odd and k In number theory, Proth's theorem is a primality test for Proth numbers....
- PseudoprimePseudoprimeIn number theory, the Fermat pseudoprimes make up the most important class of pseudoprimes that come from Fermat's little theorem.- Definition :...
- Primality testPrimality testA primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
- Constructible polygonConstructible polygonIn mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not....
: which regular polygons are constructible partially depends on Fermat primes. - Sierpiński number
- Sylvester's sequenceSylvester's sequenceIn number theory, Sylvester's sequence is an integer sequence in which each member of the sequence is the product of the previous members, plus one. The first few terms of the sequence are:...
- Double exponential function
External links
- Chris Caldwell, The Prime Glossary: Fermat number at The Prime PagesPrime pagesThe Prime Pages is a website about prime numbers maintained by Chris Caldwell at the University of Tennessee at Martin.The site maintains the list of the "5,000 largest known primes", selected smaller primes of special forms, and many "top twenty" lists for primes of various forms...
. - Luigi Morelli, History of Fermat Numbers
- John Cosgrave, Unification of Mersenne and Fermat Numbers
- Wilfrid Keller, Prime Factors of Fermat Numbers
- Yves Gallot, Generalized Fermat Prime Search
- Mark S. Manasse, Complete factorization of the ninth Fermat number (original announcement)
-