FO (complexity)
Encyclopedia
FO is the complexity class
of structures which can be recognised by formulae of first-order logic
. It is the foundation of the field of descriptive complexity
and is equal to the complexity class AC0
FO-regular. Various extensions of FO, formed by the addition of certain operators, give rise to other well-known complexity classes, allowing the complexity of some problems to be proven without having to go to the algorithmic level.
. Usually the input is either a string (of bits or over an alphabet) the elements of which are positions of the string, or a graph of which the elements are vertices. The length of the input will be measured by the size of the respective structure.
Whatever the structure is, we can assume that there are relations that can be tested, for example "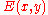
is true iff
there is an edge from
to 
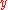" (in case of the structure being a graph), or "
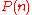is true iff
the
th letter of the string is 1." These relations are the predicates for the first-order logic system. We also have constants, which are special elements of the respective structure, for example if we want to check reachability in a graph, we will have to choose two constants s (start) and t (terminal).
In descriptive complexity theory we almost always suppose that there is a total order over the elements and that we can check equality between elements. This lets us consider elements as numbers: the element
represents the number 
iff there are 
elements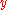 
with 
. Thanks to this we also want the primitive "bit", where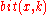 
is true if only the 
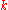th bit of 
is 1. (We can replace addition and multiplication by ternary relations such that 
is true iff 
and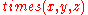 
is true iff 
).
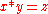), negation (
) and universal quantification (
) over elements of the structures. We also often use existential quantification (
) and disjunction (
) but those can be defined by means of the first 3 symbols.
The semantics of the formulae in FO is straightforward,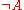
is true iff 
is false, 
is true iff 
is true and 
is true, and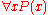 
is true iff 
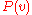is true for all values 
that 
may take in the underlying universe.
, since those primitive functions can be calculated in most of the small complexity classes.
FO without those primitives is more studied in finite model theory, and it is equivalent to smaller complexity classes; those classes are the one decided by relational machine.
. The difference between those two problems is that in QBF the size of the problem is the size of the formula and elements are just boolean values, whereas in FO the size of the problem is the size of the structure and the formula is fixed.
This is similar to Parameterized complexity
but the size of the formula is not a fixed parameter.
(where all quantifiers are written first, followed a quantifier-free formula).
, FO can be shown to be equal to AC0
, the first class in the AC
hierarchy. Indeed, there is a natural translation from FO's symbols to nodes of circuits, with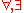
being 
and 
of size 
.
Let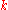
be an integer, 
be vectors of 
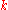variables, 
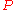be a second-order variable of arity 
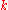, and 
be a FO(PFP) function using 
and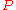 
as variables. We can iteratively define 
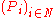such that 
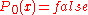and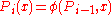 
(meaning 
with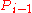 
substituted for the second-order variable 
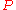). Then, either there is a fixed point, or the list of 
s is cyclic.
PFP(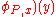
is defined as the value of the fixed point of 
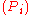on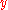 
if there is a fixed point, else as false. Since 
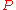s are properties of arity 
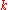, there are at most 
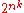values for the 
s, so with a polynomial-space counter we can check if there is a loop or not.
It has been proven that FO(PFP) is equal to PSPACE
. This definition is equivalent to FO(
).
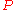, then 
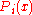always implies 
.
We can guarantee monotonicity by restricting the formula
to only contain positive occurrences of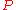 
(that is, occurrences preceded by an even number of negations). We can alternatively describe LFP(
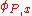) as PFP(
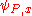) where 
.
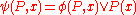Due to monotonicity, we only add vectors to the truth table of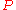
, and since there are only 
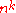possible vectors we will always find a fixed point before 
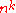iterations. Hence it can be shown that FO(LFP)=P
. This definition is equivalent to FO(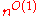
).
TC is defined this way: let
be a positive integer and 
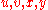be vector of 
variables. Then TC(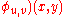
is true if there exist 
vectors of variables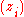 
such that 
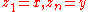, and for all 
, 
is true. Here, 
is a formula written in FO(TC) and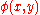 
means that the variables 
and 
are replaced by 
and 
.
This class is equal to NL
.
), we know that for all 
, there exists at most one 
such that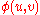 
.
We can suppose that DTC(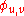
) is syntactic sugar
for TC(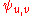
) where 
.
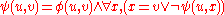It has been shown that this class is equal to L
.
)
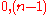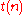]'; here 
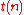is a (class of) functions from integers to integers, and for different classes of functions 
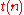we will obtain different complexity classes FO[
].
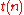In this section we will write
to mean 
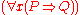and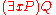 
to mean 
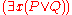. We first need to define quantifier blocks (QB), a quantifier block is a list 
where the 
s are quantifier-free FO-formulae and 
s are either 
or 
.
If
is a quantifiers block then we will call 
the iteration operator, which is defined as 
written 
time. One should pay attention that here there are 
quantifiers in the list, but only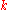 
variables and each of those variable are used 
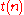times.
We can now define FO[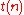
] to be the FO-formulae with an iteration operator whose exponent is in the class 
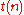, and we obtain those equalities:
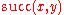is true if and only if 
.
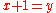Over first order logic, succ is strictly less expressive than <, which is less expressive than +, which is less expressive than bit. + and
are as expressive as bit.
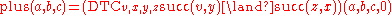and
with
This just means that when we query for bit 0 we check the parity, and go to (1,0) if
is odd(which is an accepting state), else we reject. If we check a bit 
, we divide 
by 2 and check bit 
.
Hence it makes no sense to speak of operators with successor alone, without the other predicates.
, < or bit, the equality becomes that FO(LFP) is equal to relational-P and FO(PFP) is relational-PSPACE, the classes P and PSPACE over relational machines.
The Abiteboul-Vianu Theorem states that FO(LFP)=FO(PFP) if and only if FO(<,LFP)=FO(<,PFP), hence if and only if P=PSPACE. This result has been extended to other fixpoints. This shows that the order problem in first order is more a technical problem than a fundamental one.
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
of structures which can be recognised by formulae of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
. It is the foundation of the field of descriptive complexity
Descriptive complexity
Descriptive complexity is a branch of computational complexity theory and of finite model theory that characterizes complexity classes by the type of logic needed to express the languages in them. For example, PH, the union of all complexity classes in the polynomial hierarchy, is precisely the...
and is equal to the complexity class AC0
AC0
AC0 is a complexity class used in circuit complexity. It is the smallest class in the AC hierarchy, and consists of all families of circuits of depth O and polynomial size, with unlimited-fanin AND gates and OR gates....
FO-regular. Various extensions of FO, formed by the addition of certain operators, give rise to other well-known complexity classes, allowing the complexity of some problems to be proven without having to go to the algorithmic level.
The idea
When we use the logic formalism to describe a computational problem, the input is a finite structure, and the elements of that structure are the domain of discourseDomain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
. Usually the input is either a string (of bits or over an alphabet) the elements of which are positions of the string, or a graph of which the elements are vertices. The length of the input will be measured by the size of the respective structure.
Whatever the structure is, we can assume that there are relations that can be tested, for example "
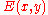is true iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
there is an edge from
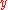to " (in case of the structure being a graph), or " 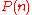is true iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
the
th letter of the string is 1." These relations are the predicates for the first-order logic system. We also have constants, which are special elements of the respective structure, for example if we want to check reachability in a graph, we will have to choose two constants s (start) and t (terminal).In descriptive complexity theory we almost always suppose that there is a total order over the elements and that we can check equality between elements. This lets us consider elements as numbers: the element
represents the number iff there are elements 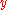with . Thanks to this we also want the primitive "bit", where 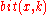is true if only the 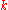th bit of is 1. (We can replace addition and multiplication by ternary relations such that is true iff and 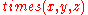is true iff 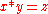).Formally
The language FO is then defined as the closure by conjunction (), negation () and universal quantification () over elements of the structures. We also often use existential quantification () and disjunction () but those can be defined by means of the first 3 symbols.The semantics of the formulae in FO is straightforward,
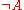is true iff is false, is true iff is true and is true, and 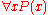is true iff 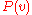is true for all values that may take in the underlying universe.Justification
Since in a computer elements are only pointers, i.e. strings of bits, in descriptive complexity the assumptions that we have an order over the element of the structures make sense. For the same reason we often suppose either a BIT predicate or + and, since those primitive functions can be calculated in most of the small complexity classes.FO without those primitives is more studied in finite model theory, and it is equivalent to smaller complexity classes; those classes are the one decided by relational machine.
Warning
A query in FO will then be to check if a first-order formula is true over a given structure representing the input to the problem. One should not confuse this kind of problem with checking if a quantified boolean formula is true, which is the definition of QBF, which is PSPACE-completePSPACE-complete
In complexity theory, a decision problem is PSPACE-complete if it is in the complexity class PSPACE, and every problem in PSPACE can be reduced to it in polynomial time...
. The difference between those two problems is that in QBF the size of the problem is the size of the formula and elements are just boolean values, whereas in FO the size of the problem is the size of the structure and the formula is fixed.
This is similar to Parameterized complexity
Parameterized complexity
Parameterized complexity is a branch of computational complexity theory in computer science that focuses on classifying computational problems according to their inherent difficulty with respect to multiple parameters of the input. The complexity of a problem is then measured as a function in those...
but the size of the formula is not a fixed parameter.
Normal form
Every formula is equivalent to a formula in prenex normal formPrenex normal form
A formula of the predicate calculus is in prenex normal form if it is written as a string of quantifiers followed by a quantifier-free part .Every formula in classical logic is equivalent to a formula in prenex normal form...
(where all quantifiers are written first, followed a quantifier-free formula).
FO without any operators
In circuit complexityCircuit complexity
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of Boolean circuits that compute them....
, FO can be shown to be equal to AC0
AC0
AC0 is a complexity class used in circuit complexity. It is the smallest class in the AC hierarchy, and consists of all families of circuits of depth O and polynomial size, with unlimited-fanin AND gates and OR gates....
, the first class in the AC
AC (complexity)
In circuit complexity, AC is a complexity class hierarchy. Each class, ACi, consists of the languages recognized by Boolean circuits with depth O and a polynomial number of unlimited-fanin AND and OR gates....
hierarchy. Indeed, there is a natural translation from FO's symbols to nodes of circuits, with
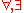being and of size .Partial fixed point is PSPACE
FO(PFP) is the set of boolean queries definable in FO where we add a partial fixed point operator.Let
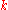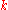be an integer, be vectors of variables, 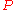be a second-order variable of arity 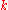, and be a FO(PFP) function using and 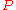as variables. We can iteratively define 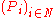such that 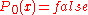and 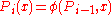(meaning with 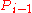substituted for the second-order variable 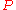). Then, either there is a fixed point, or the list of s is cyclic.PFP(
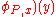is defined as the value of the fixed point of 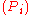on 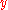if there is a fixed point, else as false. Since 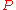s are properties of arity 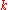, there are at most 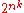values for the s, so with a polynomial-space counter we can check if there is a loop or not.It has been proven that FO(PFP) is equal to PSPACE
PSPACE
In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
. This definition is equivalent to FO(
).Least Fixed Point is P
FO(LFP) is the set of boolean queries definable in FO(PFP) where the partial fixed point is limited to be monotone. That is, if the second order variable is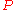, then 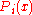always implies .We can guarantee monotonicity by restricting the formula
to only contain positive occurrences of 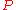(that is, occurrences preceded by an even number of negations). We can alternatively describe LFP(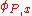) as PFP(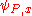) where 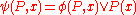.Due to monotonicity, we only add vectors to the truth table of
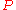, and since there are only 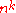possible vectors we will always find a fixed point before 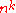iterations. Hence it can be shown that FO(LFP)=PP (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
. This definition is equivalent to FO(
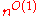).Transitive closure is NL
FO(TC) is the set of boolean queries definable in FO with a transitive closure (TC) operator.TC is defined this way: let
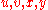be a positive integer and be vector of variables. Then TC(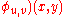 is true if there exist vectors of variables 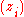such that 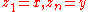, and for all , is true. Here, is a formula written in FO(TC) and 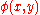means that the variables and are replaced by and .This class is equal to NL
NL (complexity)
In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space....
.
Deterministic transitive closure is L
FO(DTC) is defined as FO(TC) where the transitive closure operator is deterministic. This means that when we apply DTC(), we know that for all , there exists at most one such that 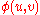.We can suppose that DTC(
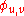) is syntactic sugarSyntactic sugar
Syntactic sugar is a computer science term that refers to syntax within a programming language that is designed to make things easier to read or to express....
for TC(
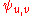) where 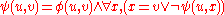.It has been shown that this class is equal to L
L (complexity)
In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space...
.
Normal form
Any formula with a fixed point (resp. transitive cosure) operator can without loss of generality be written with exactly one application of the operators applied to 0 (resp.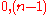)Iterating
We will define first-order with iteration, 'FO[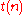]'; here 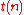is a (class of) functions from integers to integers, and for different classes of functions 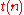we will obtain different complexity classes FO[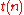].In this section we will write
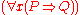to mean and 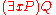to mean 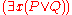. We first need to define quantifier blocks (QB), a quantifier block is a list where the s are quantifier-free FO-formulae and s are either or .If
is a quantifiers block then we will call the iteration operator, which is defined as written time. One should pay attention that here there are quantifiers in the list, but only 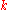variables and each of those variable are used 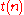times.We can now define FO[
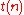] to be the FO-formulae with an iteration operator whose exponent is in the class 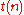, and we obtain those equalities:
- FO[
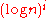] is equal to FO-uniform ACiAC (complexity)In circuit complexity, AC is a complexity class hierarchy. Each class, ACi, consists of the languages recognized by Boolean circuits with depth O and a polynomial number of unlimited-fanin AND and OR gates....
, and in fact FO[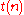
] is FO-uniform AC of depth 
. - FO[
] is equal to NC. - FO[
] is equal to PTIMEP (complexity)In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
, it is also another way to write |FO(LFP). - FO[
] is equal to PSPACEPSPACEIn computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
, it is also another way to write FO(PFP).
Logic without arithmetical relations
Let the successor relation, succ, be a binary relation such that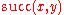 is true if and only if 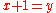.Over first order logic, succ is strictly less expressive than <, which is less expressive than +, which is less expressive than bit. + and
are as expressive as bit.Using successor to define bit
It is possible to define the plus and then the bit relations with a deterministic transitive closure.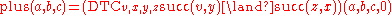 and withThis just means that when we query for bit 0 we check the parity, and go to (1,0) if
is odd(which is an accepting state), else we reject. If we check a bit , we divide by 2 and check bit .Hence it makes no sense to speak of operators with successor alone, without the other predicates.
Logics without successor
On logic without succ, +,, < or bit, the equality becomes that FO(LFP) is equal to relational-P and FO(PFP) is relational-PSPACE, the classes P and PSPACE over relational machines.The Abiteboul-Vianu Theorem states that FO(LFP)=FO(PFP) if and only if FO(<,LFP)=FO(<,PFP), hence if and only if P=PSPACE. This result has been extended to other fixpoints. This shows that the order problem in first order is more a technical problem than a fundamental one.
External links
- Neil Immerman's descriptive complexity page, including a diagram
- zoo about FO, see the class under it also