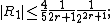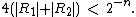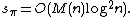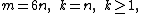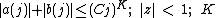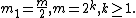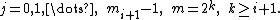FEE method
Encyclopedia
In mathematics, the FEE method is the method of fast summation of series of a special form. It was constructed in 1990 by E. A. Karatsuba and was called FEE—Fast E-function Evaluation—because it makes it possible fast computations of the Siegel  -functions, and in particular,
-functions, and in particular, 
A class of functions, which are 'similar to the exponential function' was given the name 'E-functions' by Siegel
. Among these functions are such special functions
as the hypergeometric function, cylinder
, spherical
functions and so on.
Using the FEE, it is possible to prove the following theorem
Theorem: Let be an elementary Transcendental function
be an elementary Transcendental function
, that is the exponential function
, or a
trigonometric function, or an elementary algebraic function
, or their superposition, or their inverse
, or a superposition of the inverses. Then
 -functions, and in particular,
-functions, and in particular, 
A class of functions, which are 'similar to the exponential function' was given the name 'E-functions' by Siegel
Carl Ludwig Siegel
Carl Ludwig Siegel was a mathematician specialising in number theory and celestial mechanics. He was one of the most important mathematicians of the 20th century.-Biography:...
. Among these functions are such special functions
Special functions
Special functions are particular mathematical functions which have more or less established names and notations due to their importance in mathematical analysis, functional analysis, physics, or other applications....
as the hypergeometric function, cylinder
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
, spherical
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
functions and so on.
Using the FEE, it is possible to prove the following theorem
Theorem: Let
 be an elementary Transcendental function
be an elementary Transcendental functionTranscendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
, that is the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
, or a
trigonometric function, or an elementary algebraic function
Algebraic function
In mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
, or their superposition, or their inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
, or a superposition of the inverses. Then
-
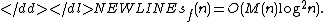
Here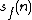 is the complexity of computation (bit) of the function
is the complexity of computation (bit) of the function 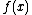 with accuracy up to
with accuracy up to  digits,
digits,  is the complexity of multiplication of two
is the complexity of multiplication of two  -digit integers.
-digit integers.
The algorithms based on the method FEE include the algorithms for fast calculation of any elementary Transcendental functionTranscendental functionA transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
for any value of the argument, the classical constants eE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
,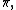 Pi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
Pi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
the Euler constantEuler–Mascheroni constantThe Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
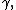 the Catalan and the Apéry constantsApéry's constantIn mathematics, Apéry's constant is a number that occurs in a variety of situations. It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics...
the Catalan and the Apéry constantsApéry's constantIn mathematics, Apéry's constant is a number that occurs in a variety of situations. It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics...
, such higher transcendental functions as the Euler gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
and its derivatives, the hypergeometric, sphericalSpherical harmonicsIn mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
, cylinder (including the BesselBessel functionIn mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
) functions and some other functions for
algebraicAlgebraic numberIn mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
values of the argument and parameters, the Riemann zeta function for integer values of the argument and the Hurwitz zeta function for integer argument and algebraic values of the parameter, and also such special integrals as the integral of probabilityError functionIn mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
, the Fresnel integralFresnel integral250px|thumb|S and C The maximum of C is about 0.977451424. If πt²/2 were used instead of t², then the image would be scaled vertically and horizontally ....
s, the integral exponential functionExponential integralIn mathematics, the exponential integral is a special function defined on the complex plane given the symbol Ei.-Definitions:For real, nonzero values of x, the exponential integral Ei can be defined as...
, the trigonometric integralTrigonometric integralIn mathematics, the trigonometric integrals are a family of integrals which involve trigonometric functions. A number of the basic trigonometric integrals are discussed at the list of integrals of trigonometric functions.-Sine integral:...
s, and some other integrals for algebraic values of the argument with the complexity bound which is close to the optimal one, namely
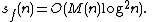
At present, only the FEE makes it possible to calculate fast the values of the functions from the class of higher transcendental functions, certain special integrals of mathematical physics and such classical constants as Euler's, Catalan's and Apery's constants. An additional advantage of the method FEE is the possibility of parallelizing the algorithms based on the FEE.
FEE-computation of classical constants
For fast evaluation of the
constant one can use the Euler formula
one can use the Euler formula
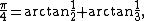
and apply the FEE to sum the Taylor series for
-
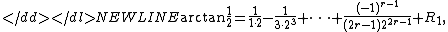
-

with the remainder terms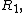
 which satisfy the bounds
which satisfy the bounds
and for
To calculate by the
by the
FEE it is possible to use also other approximations In all cases the complexity is
To compute the Euler constant gamma with accuracy up to
digits, it is necessary to sum by the FEE two series. Namely, for
-

The complexity is
To evaluate fast the constant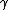
it is possible to apply the
FEE to other approximations.
FEE-computation of certain power series
By the FEE the two following series are calculated fast:
-
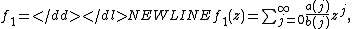
-
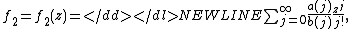
under the assumption that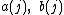 are
are
integers,
and are constants, and
are constants, and  is an algebraic number. The complexity of the evaluation of the series is
is an algebraic number. The complexity of the evaluation of the series is
-
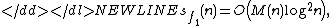
-
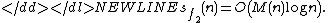
The FEE details on the example of fast calculation of the classical constant e
For the evaluation of the constant take
take  , terms of the Taylor series for
, terms of the Taylor series for 
-
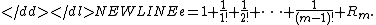
Here we choose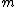 , requiring that for the remainder
, requiring that for the remainder 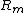 the
the
inequality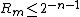 is fulfilled. This is the case, for
is fulfilled. This is the case, for
example, when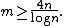 Thus, we take
Thus, we take 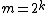
such that the natural number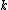 is determined by the
is determined by the
inequalities:
-
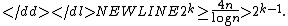
We calculate the sum
-
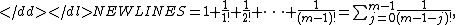
in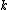 steps of the following process.
steps of the following process.
Step 1. Combining in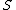 the summands sequentially in pairs we
the summands sequentially in pairs we
carry out of the brackets the "obvious" common factor and obtain
-
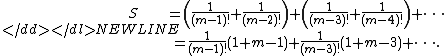
We shall compute only integer values of the expressions in the
parentheses, that is the values
-
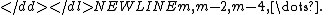
Thus, at the first step the sum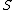 is into
is into
-

At the first step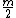 integers of the form
integers of the form
-
are calculated. After that we act in a similar way: combining on
each step the summands of the sum sequentially in pairs, we
sequentially in pairs, we
take out of the brackets the 'obvious' common factor and compute
only the integer values of the expressions in the brackets. Assume
that the first steps of this process are completed.
steps of this process are completed.
Step (
( ).
).
-
-
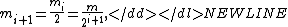
we compute only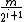 integers of the form
integers of the form
-

Here
is the product of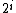 integers.
integers.
Etc.
Step , the last one. We compute one integer value
, the last one. We compute one integer value
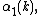 we compute, using the fast algorithm described
we compute, using the fast algorithm described
above the value and make one division of the integer
and make one division of the integer
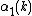 by the integer
by the integer 
with accuracy up to
digits. The obtained result is the sum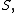 or the constant
or the constant  up
up
to digits. The complexity of all computations is
digits. The complexity of all computations is
-
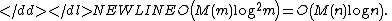
External links
- http://www.ccas.ru/personal/karatsuba/divcen.htm
- http://www.ccas.ru/personal/karatsuba/algen.htm
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-