
Exclusive disjunction
Encyclopedia
 |
| Venn diagram Venn diagram Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn... of  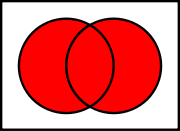 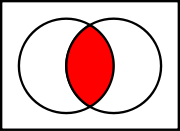  |
| Venn diagram Venn diagram Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn... of    |
The logical operation
Logical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
exclusive disjunction, also called exclusive or (symbolized
Table of logic symbols
In logic, a set of symbols is commonly used to express logical representation. As logicians are familiar with these symbols, they are not explained each time they are used. So, for students of logic, the following table lists many common symbols together with their name, pronunciation and related...
by the prefix operator J, or by the infix operators XOR, EOR, EXOR, ⊻ or ⊕, icon or ˈ), is a type of logical disjunction
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
on two operands that results in a value of true
True
True may refer to:* Truth, the state of being in accord with fact or reality-Music:* True , 1996* True , 2002* True , 1983** "True"...
if exactly one of the operands has a value of true. A simple way to state this is "one or the other but not both."
Put differently, exclusive disjunction is a logical operation on two logical value
Logical value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...
s, typically the values of two proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s, that produces a value of true only in cases where the truth value of the operands differ.
Truth table
The truth tableTruth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their...
of
 (also written as
(also written as  or
or 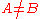 ) is as follows:
) is as follows:| Input | Output | |
|---|---|---|
| A | B | |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Equivalencies, elimination, and introduction
The exclusive disjunction , or Jpq, can be expressed in terms of the logical conjunction
, or Jpq, can be expressed in terms of the logical conjunctionLogical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
(
 ), the disjunction (
), the disjunction ( ), and the negation
), and the negationNegation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
(
 ) as follows:
) as follows:
-

The exclusive disjunction can also be expressed in the following way:
can also be expressed in the following way:
-
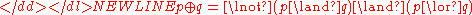
This representation of XOR may be found useful when constructing a circuit or network, because it has only one operation and small number of
operation and small number of  and
and  operations. The proof of this identity is given below:
operations. The proof of this identity is given below:
-

It is sometimes useful to write in the following way:
in the following way:
-

This equivalence can be established by applying De Morgan's laws twice to the fourth line of the above proof.
The exclusive or is also equivalent to the negation of a logical biconditionalLogical biconditionalIn logic and mathematics, the logical biconditional is the logical connective of two statements asserting "p if and only if q", where q is a hypothesis and p is a conclusion...
, by the rules of material implication (a material conditionalMaterial conditionalThe material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
is equivalent to the disjunction of the negation of its antecedentAntecedentAn antecedent is a preceding event, condition, cause, phrase, or word. It may refer to:* Antecedent moisture, a hydrologic term describing the relative wetness condition of a sewershed.* Antecedent , the first half of a hypothetical proposition....
and its consequence) and material equivalenceIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
.
In summary, we have, in mathematical and in engineering notation:-

Relation to modern algebra
Although the operatorsOperation (mathematics)The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
 (conjunctionLogical conjunctionIn logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
(conjunctionLogical conjunctionIn logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
) and (disjunctionLogical disjunctionIn logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
(disjunctionLogical disjunctionIn logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
) are very useful in logic systems, they fail a more generalizable structure in the following way:
The systems and
and 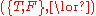 are monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
are monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s. This unfortunately prevents the combination of these two systems into larger structures, such as a mathematical ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
.
However, the system using exclusive or is an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
is an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. The combination of operators and
and  over elements
over elements  produce the well-known fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
produce the well-known fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
 GF(2)GF is the Galois field of two elements. It is the smallest finite field.- Definition :The two elements are nearly always called 0 and 1, being the additive and multiplicative identities, respectively...
GF(2)GF is the Galois field of two elements. It is the smallest finite field.- Definition :The two elements are nearly always called 0 and 1, being the additive and multiplicative identities, respectively...
. This field can represent any logic obtainable with the system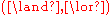 and has the added benefit of the arsenal of algebraic analysis tools for fields.
and has the added benefit of the arsenal of algebraic analysis tools for fields.
More specifically, if one associates with 0 and
with 0 and  with 1, one can interpret the logical "AND" operation as multiplication on
with 1, one can interpret the logical "AND" operation as multiplication on  and the "XOR" operation as addition on
and the "XOR" operation as addition on  :
:

Exclusive "or" in English
The Oxford English Dictionary explains "either ... or" as follows:- The primary function of either, etc., is to emphasize the indifference of the two (or more) things or courses ... but a secondary function is to emphasize the mutual exclusiveness, = either of the two, but not both.
The exclusive-or explicitly states "one or the other, but not neither nor both."
Following this kind of common-sense intuition about "or", it is sometimes argued that in many natural languages, EnglishEnglish languageEnglish is a West Germanic language that arose in the Anglo-Saxon kingdoms of England and spread into what was to become south-east Scotland under the influence of the Anglian medieval kingdom of Northumbria...
included, the word "or" has an "exclusive" sense. The exclusive disjunction of a pair of propositions, (p, q), is supposed to mean that p is true or q is true, but not both. For example, it might be argued that the normal intention of a statement like "You may have coffee, or you may have tea" is to stipulate that exactly one of the conditions can be true. Certainly under many circumstances a sentence like this example should be taken as forbidding the possibility of one's accepting both options. Even so, there is good reason to suppose that this sort of sentence is not disjunctive at all. If all we know about some disjunction is that it is true overall, we cannot be sure that either of its disjuncts is true. For example, if a woman has been told that her friend is either at the snack bar or on the tennis court, she cannot validly infer that he is on the tennis court. But if her waiter tells her that she may have coffee or she may have tea, she can validly infer that she may have tea. Nothing classically thought of as a disjunction has this property. This is so even given that she might reasonably take her waiter as having denied her the possibility of having both coffee and tea.
(Note: If the waiter intends that choosing neither tea nor coffee is an option i.e. ordering nothing, the appropriate operator is NAND: p NAND q.)
In English, the construct "either ... or" is usually used to indicate exclusive or and "or" generally used for inclusive. But in Spanish, the word "o" (or) can be used in the form p o q (exclusive) or the form o p o q (inclusive). Formalists may contend that any binary or other n-aryArityIn logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
exclusive "or" is true if and only if it has an odd number of true inputs, and there is no word in English that can conjoin a list of two or more options has this general property. For example, Barrett and Stenner contend in the 1971 article "The Myth of the Exclusive 'Or (Mind, 80 (317), 116–121) that no author has produced an example of an English or-sentence that appears to be false because both of its inputs are true, and brush off or-sentences such as "The light bulb is either on or off" as reflecting particular facts about the world rather than the nature of the word "or". However, the "barber paradox" -- Everybody in town shaves himself or is shaved by the barber, who shaves the barber? -- would not be paradoxical if "or" could not be exclusive (although a purist could say that "either" is required in the statement of the paradox).
Whether these examples can be considered "natural language" is another question. Certainly when one sees a menu stating "Lunch special: sandwich and soup or salad", one would not expect to be permitted to order both soup and salad. Nor would one expect to order neither soup nor salad, because that belies the nature of the "special", that ordering the two items together is cheaper than ordering them a la carte. Similarly, a lunch special consisting of one meat, french fries or mashed potatoes and vegetable would consist of three items, only one of which would be a form of potato. If one wanted to have meat and both kinds of potatoes, one would ask if it were possible to substitute a second order of potatoes for the vegetable. And, one would not expect to be permitted to have both types of potato and vegetable, because the result would be a vegetable plate rather than a meat plate.
Alternative symbols
The symbol used for exclusive disjunction varies from one field of application to the next, and even depends on the properties being emphasized in a given context of discussion. In addition to the abbreviation "XOR", any of the following symbols may also be seen:- A plus sign (
 ). This makes sense mathematically because exclusive disjunction corresponds to additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
). This makes sense mathematically because exclusive disjunction corresponds to additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
moduloModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
2, which has the following addition table, clearly isomorphicIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the one above:
Addition Modulo 2 
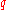

0 0 0 0 1 1 1 0 1 1 1 0
- The use of the plus sign has the added advantage that all of the ordinary algebraic properties of mathematical ringsRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
and fieldsField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
can be used without further ado. However, the plus sign is also used for Inclusive disjunction in some notation systems. - A plus sign that is modified in some way, such as being encircled (
 ). This usage faces the objection that this same symbol is already used in mathematics for the direct sumDirect sum of modulesIn abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
). This usage faces the objection that this same symbol is already used in mathematics for the direct sumDirect sum of modulesIn abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of algebraic structures. - A prefixed J, as in Jpq.
- An inclusive disjunction symbol (
 ) that is modified in some way, such as being underlined (
) that is modified in some way, such as being underlined ( ) or with dot above (
) or with dot above ( ).
). - In several programming languageProgramming languageA programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s, such as CC (programming language)C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
, C++C++C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
, C#, JavaJava (programming language)Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
, PerlPerlPerl is a high-level, general-purpose, interpreted, dynamic programming language. Perl was originally developed by Larry Wall in 1987 as a general-purpose Unix scripting language to make report processing easier. Since then, it has undergone many changes and revisions and become widely popular...
, MATLABMATLABMATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
, and PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
, a caretCaretCaret usually refers to the spacing symbol ^ in ASCII and other character sets. In Unicode, however, the corresponding character is , whereas the Unicode character named caret is actually a similar but lowered symbol: ....
(^) is used to denote the bitwise XOR operator. This is not used outside of programming contexts because it is too easily confused with other uses of the caret. - The symbol , sometimes written as >< or as >-<.
- In IEC symbology, an exclusive or is marked "=1".
Properties
Commutativity: yes





Associativity: yes










Distributivity: with no binary function, not even with itself
IdempotencyIdempotenceIdempotence is the property of certain operations in mathematics and computer science, that they can be applied multiple times without changing the result beyond the initial application...
: no










Monotonicity: no







Truth-preserving: no
When all inputs are true, the output is not true.





Falsehood-preserving: yes
When all inputs are false, the output is false.





Walsh spectrumHadamard transformThe Hadamard transform is an example of a generalized class of Fourier transforms...
: (2,0,0,-2)
Non-linearity: 0 (the function is linear)
If using binaryBinary numeral systemThe binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
values for true (1) and false (0), then exclusive or works exactly like additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
moduloModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
2.
Computer science

Bitwise operation
Exclusive disjunction is often used for bitwise operations. Examples:- 1 xor 1 = 0
- 1 xor 0 = 1
- 0 xor 1 = 1
- 0 xor 0 = 0
- 1110 xor 1001 = 0111 (this is equivalent to addition without carry)
As noted above, since exclusive disjunction is identical to addition modulo 2, the bitwise exclusive disjunction of two n-bit strings is identical to the standard vector of addition in the vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
 .
.
In computer science, exclusive disjunction has several uses:- It tells whether two bits are unequal.
- It is an optional bit-flipper (the deciding input chooses whether to invert the data input).
- It tells whether there is an odd number of 1 bits (
 is true iffIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
is true iffIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
an odd number of the variables are true).
In logical circuits, a simple adderAdder (electronics)In electronics, an adder or summer is a digital circuit that performs addition of numbers.In many computers and other kinds of processors, adders are used not only in the arithmetic logic unit, but also in other parts of the processor, where they are used to calculate addresses, table indices, and...
can be made with an XOR gateXOR gateThe XOR gate is a digital logic gate that implements an exclusive or; that is, a true output results if one, and only one, of the inputs to the gate is true . If both inputs are false or both are true , a false output results. Its behavior is summarized in the truth table shown on the right...
to add the numbers, and a series of AND, OR and NOT gates to create the carry output.
On some computer architectures, it is more efficient to store a zero in a register by xor-ing the register with itself (bits xor-ed with themselves are always zero) instead of loading and storing the value zero.
In simple threshold activated neural networkNeural networkThe term neural network was traditionally used to refer to a network or circuit of biological neurons. The modern usage of the term often refers to artificial neural networks, which are composed of artificial neurons or nodes...
s, modeling the 'xor' function requires a second layer because 'xor' is not a linearly-separable function.
Exclusive-or is sometimes used as a simple mixing function in cryptographyCryptographyCryptography is the practice and study of techniques for secure communication in the presence of third parties...
, for example, with one-time padOne-time padIn cryptography, the one-time pad is a type of encryption, which has been proven to be impossible to crack if used correctly. Each bit or character from the plaintext is encrypted by a modular addition with a bit or character from a secret random key of the same length as the plaintext, resulting...
or Feistel networkFeistel cipherIn cryptography, a Feistel cipher is a symmetric structure used in the construction of block ciphers, named after the German-born physicist and cryptographer Horst Feistel who did pioneering research while working for IBM ; it is also commonly known as a Feistel network. A large proportion of block...
systems.
XOR is used in RAIDRAIDRAID is a storage technology that combines multiple disk drive components into a logical unit...
3–6 for creating parity information. For example, RAID can "back up" bytes10011100and01101100from two (or more) hard drives by XORing (11110000) and writing to another drive. Under this method, if any one of the three hard drives are lost, the lost byte can be re-created by XORing bytes from the remaining drives. If the drive containing01101100is lost,10011100and11110000can be XORed to recover the lost byte.
XOR is also used to detect an overflow in the result of a signed binary arithmetic operation. If the leftmost retained bit of the result is not the same as the infinite number of digits to the left, then that means overflow occurred. XORing those two bits will give a "1" if there is an overflow.
XOR can be used to swap two numeric variables in computers, using the XOR swap algorithmXOR swap algorithmIn computer programming, the XOR swap is an algorithm that uses the XOR bitwise operation to swap values of distinct variables having the same data type without using a temporary variable...
; however this is regarded as more of a curiosity and not encouraged in practice.
In computer graphicsComputer graphicsComputer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, XOR-based drawing methods are often used to manage such items as bounding boxesBounding volumeIn computer graphics and computational geometry, a bounding volume for a set of objects is a closed volume that completely contains the union of the objects in the set. Bounding volumes are used to improve the efficiency of geometrical operations by using simple volumes to contain more complex...
and cursorsCursor (computers)In computing, a cursor is an indicator used to show the position on a computer monitor or other display device that will respond to input from a text input or pointing device. The flashing text cursor may be referred to as a caret in some cases...
on systems without alpha channelsAlpha compositingIn computer graphics, alpha compositing is the process of combining an image with a background to create the appearance of partial or full transparency. It is often useful to render image elements in separate passes, and then combine the resulting multiple 2D images into a single, final image in a...
or overlay planes.
See also
- Affirming a disjunct
- Ampheck
- Boolean algebra (logic)
- List of Boolean algebra topics
- Boolean domainBoolean domainIn mathematics and abstract algebra, a Boolean domain is a set consisting of exactly two elements whose interpretations include false and true...
- Boolean function
- Boolean-valued functionBoolean-valued functionA boolean-valued function, in some usages is a predicate or a proposition, is a function of the type f : X → B, where X is an arbitrary set and where B is a boolean domain....
- Controlled NOT gateControlled NOT gateThe Controlled NOT gate is a quantum gate that is an essential component in the construction of a quantum computer. It can be used to disentangle EPR states...
- Disjunctive syllogismDisjunctive syllogismA disjunctive syllogism, also known as disjunction-elimination and or-elimination , and historically known as modus tollendo ponens,, is a classically valid, simple argument form:where \vdash represents the logical assertion....
- First-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
- Inclusive or
- Involution
- Logical graphLogical graphA logical graph is a special type of diagramatic structure in any one of several systems of graphical syntax that Charles Sanders Peirce developed for logic....
- Logical valueLogical valueIn logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...
- Multigrade operatorMultigrade operatorIn logic and mathematics, a multigrade operator \Omega is a parametric operator with parameter k in the set N of non-negative integers....
- OperationOperation (mathematics)The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
- Parametric operator
- Parity bitParity bitA parity bit is a bit that is added to ensure that the number of bits with the value one in a set of bits is even or odd. Parity bits are used as the simplest form of error detecting code....
- Propositional calculusPropositional calculusIn mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
- Rule 90Rule 90Rule 90 is an elementary cellular automaton based on the exclusive or function. It consists of a one-dimensional array of cells, each of which can hold either a 0 or a 1 value; in each time step all values are simultaneously replaced by the exclusive or of the two neighboring values...
- Symmetric differenceSymmetric differenceIn mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
- XOR linked listXOR linked listAn XOR linked list is a data structure used in computer programming. They take advantage of the bitwise exclusive disjunction operation, here denoted by ⊕, to decrease storage requirements for doubly linked lists. An ordinary doubly linked list stores addresses of the previous and next list items...
- XOR gateXOR gateThe XOR gate is a digital logic gate that implements an exclusive or; that is, a true output results if one, and only one, of the inputs to the gate is true . If both inputs are false or both are true , a false output results. Its behavior is summarized in the truth table shown on the right...
- XOR cipher
-
-
-
-

