
Euler's three-body problem
Encyclopedia
In physics
and astronomy
, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field
of two other point masses that are either fixed in space or move in circular coplanar orbits about their center of mass. This problem is significant as an exactly soluble special case
of the three-body problem
, and an approximate solution for particles moving in the gravitational fields of prolate and oblate spheroids. This problem is named after Leonhard Euler
, who discussed it in memoirs published in 1760. Important extensions and analyses were contributed subsequently by Lagrange
, Liouville
, Laplace
, Jacobi, Darboux
, Le Verrier, Velde, Hamilton
, Poincaré
, Birkhoff
and E. T. Whittaker
, among others.
Euler's problem also covers the case when the particle is acted upon by other inverse-square central forces, such as the electrostatic interaction
described by Coulomb's law
. The classical solutions of the Euler problem have been used to study chemical bonding, using a semiclassical approximation of the energy levels of a single electron moving in the field of two atomic nuclei, such as the diatomic ion HeH2+. This was first done by Wolfgang Pauli
in his doctoral dissertation under Arnold Sommerfeld
, a study of the first ion of molecular hydrogen, namely the Hydrogen molecule-ion H2+. These energy levels can be calculated with reasonable accuracy using the Einstein-Brillouin-Keller method
, which is also the basis of the Bohr model
of atomic hydrogen. More recently, as explained further in the quantum-mechanical version, analytical solutions to the eigenenergies have been obtained: these are a generalization of the Lambert W function.
By treating Euler's problem as a Liouville dynamical system
, the exact solution can be expressed in terms of elliptic integral
s. For convenience, the problem may also be solved by numerical methods, such as Runge–Kutta integration
of the equations of motion. The total energy of the moving particle is conserved, but its linear and angular momentum
are not, since the two fixed centers can apply a net force and torque. Nevertheless, the particle has a second conserved quantity that corresponds to the angular momentum
or to the Laplace–Runge–Lenz vector as limiting cases.
The Euler three-body problem is known by a variety of names, such as the problem of two fixed centers, the Euler-Jacobi problem, and the two-center Kepler problem. It is also called the circular restricted three-body problem, as it is a special case of the general three-body problem
in which the two massive particles have zero orbital eccentricity
and the third particle is "restricted" to have negligible mass. Special cases of this problem include the Copenhagen problem (where the two large masses are equal) and the Pythagorean problem (where the three bodies have initial masses in the ratio 3:4:5 and prescribed initial positions). Various generalizations of Euler's problem are known; these generalizations add linear and inverse cubic forces and up to five centers of force. Special cases of these generalized problems include Darboux's problem and Velde's problem.
, such as Newtonian gravity
or Coulomb's law
. Examples of Euler's problem include a planet
moving in the gravitational field of two star
s, or an electron
moving in the electric field
of two nuclei
, such as the first ion
of the hydrogen molecule
, namely the hydrogen molecule-ion H2+. The strength of the two inverse-square forces need not be equal; for illustration, the two attracting stars may have different masses, and the two nuclei may have different charges, as in the molecular ion HeH2+.
This problem was first considered by Leonhard Euler
, who showed that it had an exact solution in 1760. Joseph Louis Lagrange
solved a generalized problem in which the centers exert both linear and inverse-square forces. Carl Gustav Jacob Jacobi showed that the rotation of the particle about the axis of the two fixed centers could be separated out, reducing the general three-dimensional problem to the planar problem.
; in other words, the total energy E is a constant of motion
. The potential energy
is given by

where r represents the particle's position, and r1 and r2 are the distances between the particle and the centers of force; μ1 and μ2 are constants that measure the strength of the first and second forces, respectively. The total energy equals sum of this potential energy with the particle's kinetic energy
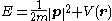
where m and p are the particle's mass and linear momentum, respectively.
The particle's linear and angular momentum
are not conserved in Euler's problem, since the two centers of force act like external forces upon the particle, which may yield a net force and torque on the particle. Nevertheless, Euler's problem has a second constant of motion
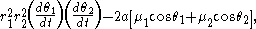
where 2a is the separation of the two centers of force, θ1 and θ2 are the angles of the lines connecting the particle to the centers of force, with respect to the line connecting the centers. This second constant of motion was identified by E. T. Whittaker
in his work on analytical mechanics, and generalized to n dimensions by Coulson
and Joseph in 1967. In the Coulson-Joseph form, the constant of motion is written
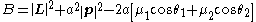
This constant of motion corresponds to the total angular momentum
|L|2 in the limit when the two centers of force converge to a single point (a → 0), and proportional to the Laplace–Runge–Lenz vector A in the limit when one of the centers goes to infinity (a→∞ while x-a remains finite).
 . Two of the three bodies are nuclei and the third is a fast moving electron. The two nuclei are 1800 times heavier than the electron and thus modeled as fixed centers. It is well known that the Schrödinger wave equation is separable in Prolate spheroidal coordinates
. Two of the three bodies are nuclei and the third is a fast moving electron. The two nuclei are 1800 times heavier than the electron and thus modeled as fixed centers. It is well known that the Schrödinger wave equation is separable in Prolate spheroidal coordinates
and can be decoupled into two ordinary differential equations coupled by the energy eigenvalue and a separation constant.
However, solutions required series expansions from basis sets. Nonetheless, through experimental mathematics
, it was found that the energy eigenvalue was mathematically a generalization of the Lambert W function
(see Lambert W function and references therein for more details). The hydrogen molecular ion in the case of clamped nuclei can be completely worked out within a Computer algebra system
. The fact that its solution is an implicit function
is revealing in itself. One of the successes of theoretical physics is not simply a matter that it is amenable to a mathematical treatment but that the algebraic equations involved can be symbolically manipulated until an analytical solution, preferably a closed form solution, is isolated. This type of solution for a special case of the three-body problem shows us the possibilities of what is possible as an anaytical solution for the quantum three-body and many-body problem.
s, with forces that are both linear and inverse-square law
s, together with a force parallel to the axis of imaginary centers and varying as the inverse cube of the distance to that axis.
The solution to the original Euler problem is an approximate solution for the motion of a particle in the gravitational field of a prolate body, i.e., a sphere that has been elongated in one direction, such as a cigar shape. The corresponding approximate solution for a particle moving in the field of an oblate spheroid (a sphere squashed in one direction) is obtained by making the positions of the two centers of force into imaginary number
s. The oblate spheroid solution is astronomically more important, since most planets, stars and galaxies are approximately oblate spheroids; prolate spheroids are very rare.
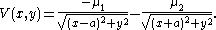
where the proportionality constants μ1 and μ2 may be positive or negative. The two centers of attraction can be considered as the foci of a set of ellipses. If either center were absent, the particle would move on one of these ellipses, as a solution of the Kepler problem
. Therefore, according to Bonnet's theorem, the same ellipses are the solutions for the Euler problem.
Introducing elliptic coordinates
,
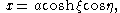
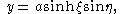
the potential energy can be written as

and the kinetic energy as
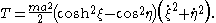
This is a Liouville dynamical system
if ξ and η are taken as φ1 and φ2, respectively; thus, the function Y equals

and the function W equals
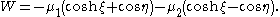
Using the general solution for a Liouville dynamical system
, one obtains
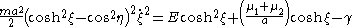
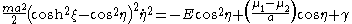
Introducing a parameter u by the formula

gives the parametric solution
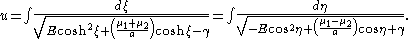
Since these are elliptic integral
s, the coordinates ξ and η can be expressed as elliptic functions of u.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
of two other point masses that are either fixed in space or move in circular coplanar orbits about their center of mass. This problem is significant as an exactly soluble special case
Special case
In logic, especially as applied in mathematics, concept A is a special case or specialization of concept B precisely if every instance of A is also an instance of B, or equivalently, B is a generalization of A. For example, all circles are ellipses ; therefore the circle is a special case of the...
of the three-body problem
Three-body problem
Three-body problem has two distinguishable meanings in physics and classical mechanics:# In its traditional sense the three-body problem is the problem of taking an initial set of data that specifies the positions, masses and velocities of three bodies for some particular point in time and then...
, and an approximate solution for particles moving in the gravitational fields of prolate and oblate spheroids. This problem is named after Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, who discussed it in memoirs published in 1760. Important extensions and analyses were contributed subsequently by Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
, Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
, Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
, Jacobi, Darboux
Jean Gaston Darboux
Jean-Gaston Darboux was a French mathematician.-Life:Darboux made several important contributions to geometry and mathematical analysis . He was a biographer of Henri Poincaré and he edited the Selected Works of Joseph Fourier.Darboux received his Ph.D...
, Le Verrier, Velde, Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
, Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
, Birkhoff
George David Birkhoff
-External links:* − from National Academies Press, by Oswald Veblen....
and E. T. Whittaker
E. T. Whittaker
Edmund Taylor Whittaker FRS FRSE was an English mathematician who contributed widely to applied mathematics, mathematical physics and the theory of special functions. He had a particular interest in numerical analysis, but also worked on celestial mechanics and the history of physics...
, among others.
Euler's problem also covers the case when the particle is acted upon by other inverse-square central forces, such as the electrostatic interaction
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
described by Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
. The classical solutions of the Euler problem have been used to study chemical bonding, using a semiclassical approximation of the energy levels of a single electron moving in the field of two atomic nuclei, such as the diatomic ion HeH2+. This was first done by Wolfgang Pauli
Wolfgang Pauli
Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...
in his doctoral dissertation under Arnold Sommerfeld
Arnold Sommerfeld
Arnold Johannes Wilhelm Sommerfeld was a German theoretical physicist who pioneered developments in atomic and quantum physics, and also educated and groomed a large number of students for the new era of theoretical physics...
, a study of the first ion of molecular hydrogen, namely the Hydrogen molecule-ion H2+. These energy levels can be calculated with reasonable accuracy using the Einstein-Brillouin-Keller method
Einstein-Brillouin-Keller method
The Einstein–Brillouin–Keller method is a semiclassical method to compute eigenvalues in quantum mechanical systems.-See also:*Quantum mechanics*WKB approximation*Albert Einstein*Léon Brillouin*Joseph B. Keller...
, which is also the basis of the Bohr model
Bohr model
In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...
of atomic hydrogen. More recently, as explained further in the quantum-mechanical version, analytical solutions to the eigenenergies have been obtained: these are a generalization of the Lambert W function.
By treating Euler's problem as a Liouville dynamical system
Liouville dynamical system
In classical mechanics, a Liouville dynamical system is an exactly soluble dynamical system in which the kinetic energy T and potential energy V can be expressed in terms of the s generalized coordinates q as follows:...
, the exact solution can be expressed in terms of elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
s. For convenience, the problem may also be solved by numerical methods, such as Runge–Kutta integration
Runge–Kutta methods
In numerical analysis, the Runge–Kutta methods are an important family of implicit and explicit iterative methods for the approximation of solutions of ordinary differential equations. These techniques were developed around 1900 by the German mathematicians C. Runge and M.W. Kutta.See the article...
of the equations of motion. The total energy of the moving particle is conserved, but its linear and angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
are not, since the two fixed centers can apply a net force and torque. Nevertheless, the particle has a second conserved quantity that corresponds to the angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
or to the Laplace–Runge–Lenz vector as limiting cases.
The Euler three-body problem is known by a variety of names, such as the problem of two fixed centers, the Euler-Jacobi problem, and the two-center Kepler problem. It is also called the circular restricted three-body problem, as it is a special case of the general three-body problem
Three-body problem
Three-body problem has two distinguishable meanings in physics and classical mechanics:# In its traditional sense the three-body problem is the problem of taking an initial set of data that specifies the positions, masses and velocities of three bodies for some particular point in time and then...
in which the two massive particles have zero orbital eccentricity
Orbital eccentricity
The orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
and the third particle is "restricted" to have negligible mass. Special cases of this problem include the Copenhagen problem (where the two large masses are equal) and the Pythagorean problem (where the three bodies have initial masses in the ratio 3:4:5 and prescribed initial positions). Various generalizations of Euler's problem are known; these generalizations add linear and inverse cubic forces and up to five centers of force. Special cases of these generalized problems include Darboux's problem and Velde's problem.
Overview and history
Euler's three-body problem is to describe the motion of a particle under the influence of two centers that attract the particle with central forces that decrease with distance as an inverse-square lawInverse-square law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
, such as Newtonian gravity
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
or Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
. Examples of Euler's problem include a planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
moving in the gravitational field of two star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s, or an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
moving in the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
of two nuclei
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
, such as the first ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
of the hydrogen molecule
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
, namely the hydrogen molecule-ion H2+. The strength of the two inverse-square forces need not be equal; for illustration, the two attracting stars may have different masses, and the two nuclei may have different charges, as in the molecular ion HeH2+.
This problem was first considered by Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, who showed that it had an exact solution in 1760. Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
solved a generalized problem in which the centers exert both linear and inverse-square forces. Carl Gustav Jacob Jacobi showed that the rotation of the particle about the axis of the two fixed centers could be separated out, reducing the general three-dimensional problem to the planar problem.
Constants of motion
The problem of two fixed centers conserves energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
; in other words, the total energy E is a constant of motion
Constant of motion
In mechanics, a constant of motion is a quantity that is conserved throughout the motion, imposing in effect a constraint on the motion. However, it is a mathematical constraint, the natural consequence of the equations of motion, rather than a physical constraint...
. The potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
is given by

where r represents the particle's position, and r1 and r2 are the distances between the particle and the centers of force; μ1 and μ2 are constants that measure the strength of the first and second forces, respectively. The total energy equals sum of this potential energy with the particle's kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
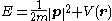
where m and p are the particle's mass and linear momentum, respectively.
The particle's linear and angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
are not conserved in Euler's problem, since the two centers of force act like external forces upon the particle, which may yield a net force and torque on the particle. Nevertheless, Euler's problem has a second constant of motion
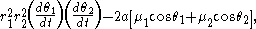
where 2a is the separation of the two centers of force, θ1 and θ2 are the angles of the lines connecting the particle to the centers of force, with respect to the line connecting the centers. This second constant of motion was identified by E. T. Whittaker
E. T. Whittaker
Edmund Taylor Whittaker FRS FRSE was an English mathematician who contributed widely to applied mathematics, mathematical physics and the theory of special functions. He had a particular interest in numerical analysis, but also worked on celestial mechanics and the history of physics...
in his work on analytical mechanics, and generalized to n dimensions by Coulson
Charles Coulson
Charles Alfred Coulson FRS was an applied mathematician, theoretical chemist and religious author.His major scientific work was as a pioneer of the application of the quantum theory of valency to problems of molecular structure, dynamics and reactivity...
and Joseph in 1967. In the Coulson-Joseph form, the constant of motion is written
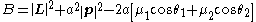
This constant of motion corresponds to the total angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
|L|2 in the limit when the two centers of force converge to a single point (a → 0), and proportional to the Laplace–Runge–Lenz vector A in the limit when one of the centers goes to infinity (a→∞ while x-a remains finite).
Quantum mechanical version
A special case of the quantum mechanical three-body problem is the Hydrogen molecule-ion . Two of the three bodies are nuclei and the third is a fast moving electron. The two nuclei are 1800 times heavier than the electron and thus modeled as fixed centers. It is well known that the Schrödinger wave equation is separable in Prolate spheroidal coordinates
. Two of the three bodies are nuclei and the third is a fast moving electron. The two nuclei are 1800 times heavier than the electron and thus modeled as fixed centers. It is well known that the Schrödinger wave equation is separable in Prolate spheroidal coordinatesProlate spheroidal coordinates
Prolate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating a spheroid around its major axis, i.e., the axis on which the foci are located...
and can be decoupled into two ordinary differential equations coupled by the energy eigenvalue and a separation constant.
However, solutions required series expansions from basis sets. Nonetheless, through experimental mathematics
Experimental mathematics
Experimental mathematics is an approach to mathematics in which numerical computation is used to investigate mathematical objects and identify properties and patterns...
, it was found that the energy eigenvalue was mathematically a generalization of the Lambert W function
(see Lambert W function and references therein for more details). The hydrogen molecular ion in the case of clamped nuclei can be completely worked out within a Computer algebra system
Computer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
. The fact that its solution is an implicit function
Implicit function
The implicit function theorem provides a link between implicit and explicit functions. It states that if the equation R = 0 satisfies some mild conditions on its partial derivatives, then one can in principle solve this equation for y, at least over some small interval...
is revealing in itself. One of the successes of theoretical physics is not simply a matter that it is amenable to a mathematical treatment but that the algebraic equations involved can be symbolically manipulated until an analytical solution, preferably a closed form solution, is isolated. This type of solution for a special case of the three-body problem shows us the possibilities of what is possible as an anaytical solution for the quantum three-body and many-body problem.
Generalizations
An exhaustive analysis of the soluble generalizations of Euler's three-body problem was carried out by Adam Hiltebeitel in 1911. The simplest generalization of Euler's three-body problem is to augment the inverse-square force laws with a force that increases linearly with distance. The next generalization is to add a third center of force midway between the original two centers, that exerts only a linear force. The final set of generalizations is to add two fixed centers of force at positions that are imaginary numberImaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
s, with forces that are both linear and inverse-square law
Inverse-square law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
s, together with a force parallel to the axis of imaginary centers and varying as the inverse cube of the distance to that axis.
The solution to the original Euler problem is an approximate solution for the motion of a particle in the gravitational field of a prolate body, i.e., a sphere that has been elongated in one direction, such as a cigar shape. The corresponding approximate solution for a particle moving in the field of an oblate spheroid (a sphere squashed in one direction) is obtained by making the positions of the two centers of force into imaginary number
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
s. The oblate spheroid solution is astronomically more important, since most planets, stars and galaxies are approximately oblate spheroids; prolate spheroids are very rare.
Original Euler problem
In the original Euler problem, the two centers of force acting on the particle are assumed to be fixed in space; let these centers be located along the x-axis at ±a. The particle is likewise assumed to be confined to a fixed plane containing the two centers of force. The potential energy of the particle in the field of these centers is given by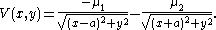
where the proportionality constants μ1 and μ2 may be positive or negative. The two centers of attraction can be considered as the foci of a set of ellipses. If either center were absent, the particle would move on one of these ellipses, as a solution of the Kepler problem
Kepler problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive...
. Therefore, according to Bonnet's theorem, the same ellipses are the solutions for the Euler problem.
Introducing elliptic coordinates
Elliptic coordinates
In geometry, the elliptic coordinate system is a two-dimensional orthogonal coordinate system in whichthe coordinate lines are confocal ellipses and hyperbolae...
,
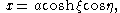
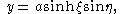
the potential energy can be written as

and the kinetic energy as
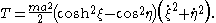
This is a Liouville dynamical system
Liouville dynamical system
In classical mechanics, a Liouville dynamical system is an exactly soluble dynamical system in which the kinetic energy T and potential energy V can be expressed in terms of the s generalized coordinates q as follows:...
if ξ and η are taken as φ1 and φ2, respectively; thus, the function Y equals

and the function W equals
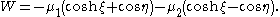
Using the general solution for a Liouville dynamical system
Liouville dynamical system
In classical mechanics, a Liouville dynamical system is an exactly soluble dynamical system in which the kinetic energy T and potential energy V can be expressed in terms of the s generalized coordinates q as follows:...
, one obtains
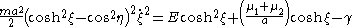
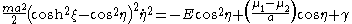
Introducing a parameter u by the formula

gives the parametric solution
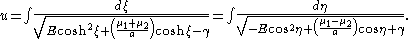
Since these are elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
s, the coordinates ξ and η can be expressed as elliptic functions of u.
See also
- Jacobi integralJacobi integralIn celestial mechanics, Jacobi's integral is the only known conserved quantity for the restricted three-body problem problem [1]; unlike in the two-body problem, the energy and momentum of the system are not conserved separately and a general analytical solution is not possible...
- Lagrangian pointLagrangian pointThe Lagrangian points are the five positions in an orbital configuration where a small object affected only by gravity can theoretically be stationary relative to two larger objects...
- Three-body problemThree-body problemThree-body problem has two distinguishable meanings in physics and classical mechanics:# In its traditional sense the three-body problem is the problem of taking an initial set of data that specifies the positions, masses and velocities of three bodies for some particular point in time and then...
- Liouville dynamical systemLiouville dynamical systemIn classical mechanics, a Liouville dynamical system is an exactly soluble dynamical system in which the kinetic energy T and potential energy V can be expressed in terms of the s generalized coordinates q as follows:...
- Hydrogen molecular ion

