Euler's formula
Encyclopedia
Euler's formula, named after Leonhard Euler
, is a mathematical
formula
in complex analysis
that establishes the deep relationship between the trigonometric functions and the complex
exponential function
. Euler's formula states that, for any real number
x,
where e is the base of the natural logarithm
, i is the imaginary unit
, and cos and sin are the trigonometric function
s cosine and sine respectively, with the argument x given in radian
s. This complex exponential function is sometimes called cis(x). The formula is still valid if x is a complex number
, and so some authors refer to the more general complex version as Euler's formula.
Richard Feynman
called Euler's formula "our jewel" and "one of the most remarkable, almost astounding, formulas in all of mathematics."
who noted that
And since
the above equation tells us something about complex logarithms. Bernoulli, however, did not evaluate the integral. His correspondence with Euler (who also knew the above equation) shows that he didn't fully understand logarithms. Euler also suggested that the complex logarithms can have infinitely many values.
Meanwhile, Roger Cotes
, in 1714, discovered that
(where "ln" means natural logarithm
, i.e. log with base e). We now know that the above equation is true modulo
integer multiples of
, but Cotes missed the fact that a complex logarithm can have infinitely many values which owes to the periodicity of the trigonometric functions.
It was Euler (presumably around 1740) who turned his attention to the exponential function instead of logarithms, and obtained the correct formula now named after him. It was published in 1748, and his proof was based on the infinite series of both sides being equal. Neither of these men saw the geometrical interpretation of the formula: the view of complex numbers as points in the complex plane
arose only some 50 years later (see Caspar Wessel
).
This formula can be interpreted as saying that the function eix traces out the unit circle
in the complex number
plane as x ranges through the real numbers. Here, x is the angle
that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counter clockwise and in radian
s.
The original proof is based on the Taylor series
expansions of the exponential function
ez (where z is a complex number) and of sin x and cos x for real numbers x (see below). In fact, the same proof shows that Euler's formula is even valid for all complex numbers z.
A point in the complex plane
can be represented by a complex number written in
cartesian coordinates. Euler's formula provides a means of conversion between cartesian coordinates and polar coordinates. The polar form simplifies the mathematics when used in multiplication or powers of complex numbers. Any complex number z = x + iy can be written as
where
the real part
the imaginary part
the magnitude
of z
atan2
(y, x) .
is the argument
of z—i.e., the angle between the x axis and the vector z measured counterclockwise and in radian
s—which is defined up to
addition of 2π. Many texts write tan-1(y/x) instead of atan2(y,x) but this needs adjustment when x ≤ 0.
Now, taking this derived formula, we can use Euler's formula to define the logarithm
of a complex number. To do this, we also use the definition of the logarithm (as the inverse operator of exponentiation) that
and that
both valid for any complex numbers a and b.
Therefore, one can write:
for any z ≠ 0. Taking the logarithm of both sides shows that:
and in fact this can be used as the definition for the complex logarithm
. The logarithm of a complex number is thus a multi-valued function, because
is multi-valued.
Finally, the other exponential law
which can be seen to hold for all integers k, together with Euler's formula, implies several trigonometric identities as well as de Moivre's formula
.
and trigonometry
, and provides an interpretation of the sine and cosine functions as weighted sums of the exponential function:
The two equations above can be derived by adding or subtracting Euler's formulas:
and solving for either cosine or sine.
These formulas can even serve as the definition of the trigonometric functions for complex arguments x. For example, letting x = iy, we have:
Complex exponentials can simplify trigonometry, because they are easier to manipulate than their sinusoidal components. One technique is simply to convert sinusoids into equivalent expressions in terms of exponentials. After the manipulations, the simplified result is still real-valued. For example:
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, is a mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
that establishes the deep relationship between the trigonometric functions and the complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
. Euler's formula states that, for any real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
x,
where e is the base of the natural logarithm
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
, i is the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
, and cos and sin are the trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s cosine and sine respectively, with the argument x given in radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s. This complex exponential function is sometimes called cis(x). The formula is still valid if x is a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, and so some authors refer to the more general complex version as Euler's formula.
Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
called Euler's formula "our jewel" and "one of the most remarkable, almost astounding, formulas in all of mathematics."
History
It was Johann BernoulliJohann Bernoulli
Johann Bernoulli was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family...
who noted that
And since
the above equation tells us something about complex logarithms. Bernoulli, however, did not evaluate the integral. His correspondence with Euler (who also knew the above equation) shows that he didn't fully understand logarithms. Euler also suggested that the complex logarithms can have infinitely many values.
Meanwhile, Roger Cotes
Roger Cotes
Roger Cotes FRS was an English mathematician, known for working closely with Isaac Newton by proofreading the second edition of his famous book, the Principia, before publication. He also invented the quadrature formulas known as Newton–Cotes formulas and first introduced what is known today as...
, in 1714, discovered that
(where "ln" means natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
, i.e. log with base e). We now know that the above equation is true modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
integer multiples of
, but Cotes missed the fact that a complex logarithm can have infinitely many values which owes to the periodicity of the trigonometric functions.It was Euler (presumably around 1740) who turned his attention to the exponential function instead of logarithms, and obtained the correct formula now named after him. It was published in 1748, and his proof was based on the infinite series of both sides being equal. Neither of these men saw the geometrical interpretation of the formula: the view of complex numbers as points in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
arose only some 50 years later (see Caspar Wessel
Caspar Wessel
Caspar Wessel was a Norwegian-Danish mathematician and cartographer. In 1799, Wessel was the first person to describe the complex numbers. He was the younger brother of poet and playwright Johan Herman Wessel....
).
Applications in complex number theory
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
in the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
plane as x ranges through the real numbers. Here, x is the angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counter clockwise and in radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s.
The original proof is based on the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansions of the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
ez (where z is a complex number) and of sin x and cos x for real numbers x (see below). In fact, the same proof shows that Euler's formula is even valid for all complex numbers z.
A point in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
can be represented by a complex number written in
cartesian coordinates. Euler's formula provides a means of conversion between cartesian coordinates and polar coordinates. The polar form simplifies the mathematics when used in multiplication or powers of complex numbers. Any complex number z = x + iy can be written as
where
the real part the imaginary part the magnitudeMagnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
of z
atan2Atan2
In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
(y, x) .
is the argumentArg (mathematics)
In mathematics, arg is a function operating on complex numbers . It gives the angle between the line joining the point to the origin and the positive real axis, shown as in figure 1 opposite, known as an argument of the point In mathematics, arg is a function operating on complex numbers...
of z—i.e., the angle between the x axis and the vector z measured counterclockwise and in radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s—which is defined up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
addition of 2π. Many texts write tan-1(y/x) instead of atan2(y,x) but this needs adjustment when x ≤ 0.
Now, taking this derived formula, we can use Euler's formula to define the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of a complex number. To do this, we also use the definition of the logarithm (as the inverse operator of exponentiation) that
and that
both valid for any complex numbers a and b.
Therefore, one can write:
for any z ≠ 0. Taking the logarithm of both sides shows that:
and in fact this can be used as the definition for the complex logarithm
Complex logarithm
In complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...
. The logarithm of a complex number is thus a multi-valued function, because
is multi-valued.Finally, the other exponential law
which can be seen to hold for all integers k, together with Euler's formula, implies several trigonometric identities as well as de Moivre's formula
De Moivre's formula
In mathematics, de Moivre's formula , named after Abraham de Moivre, states that for any complex number x and integer n it holds that...
.
Relationship to trigonometry
Euler's formula provides a powerful connection between analysisMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, and provides an interpretation of the sine and cosine functions as weighted sums of the exponential function:
The two equations above can be derived by adding or subtracting Euler's formulas:
and solving for either cosine or sine.
These formulas can even serve as the definition of the trigonometric functions for complex arguments x. For example, letting x = iy, we have:
Complex exponentials can simplify trigonometry, because they are easier to manipulate than their sinusoidal components. One technique is simply to convert sinusoids into equivalent expressions in terms of exponentials. After the manipulations, the simplified result is still real-valued. For example:
-
Another technique is to represent the sinusoids in terms of the real part of a more complex expression, and perform the manipulations on the complex expression. For example:
-
This formula is used for recursive generation of cos(nx) for integer values of n and arbitrary x (in radians).
Other applications
In differential equations, the function eix is often used to simplify derivations, even if the final answer is a real function involving sine and cosine. The reason for this is that the complex exponential is the eigenfunctionEigenfunctionIn mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
of differentiation. Euler's identity is an easy consequence of Euler's formula.
In electrical engineeringElectrical engineeringElectrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...
and other fields, signals that vary periodically over time are often described as a combination of sine and cosine functions (see Fourier analysis), and these are more conveniently expressed as the real part of exponential functions with imaginaryImaginary numberAn imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
exponents, using Euler's formula. Also, phasor analysis of circuits can include Euler's formula to represent the impedance of a capacitor or an inductor.
Definitions of complex exponentiation
The exponential function ex for real values of x may be defined in a few different equivalent ways (see Characterizations of the exponential functionCharacterizations of the exponential functionIn mathematics, the exponential function can be characterized in many ways. The following characterizations are most common. This article discusses why each characterization makes sense, and why the characterizations are independent of and equivalent to each other...
). Several of these methods may be directly extended to give definitions of ez for complex values of z simply by substituting z in place of x and using the complex algebraic operations. In particular we may use either of the two following definitions which are equivalent. From a more advanced perspective, each of these definitions may be interpreted as giving the unique analytic continuationAnalytic continuationIn complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of ex to the complex plane.
Power series definition
For complex z
Using the ratio test it is possible to show that this power series has an infinite radius of convergenceRadius of convergenceIn mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
, and so defines ez for all complex z.
Limit definition
For complex z
Using power series
Here is a proof of Euler's formula using power series expansionsTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
as well as basic facts about the powers of i:
-
and so on. Using now the power series definition from above we see that for real values of x
-
In the last step we have simply recognized the Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
for sin(x) and cos(x). The rearrangement of terms is justified because each series is absolutely convergentAbsolute convergenceIn mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
.
Using the limit definition
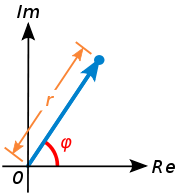Here is a proof of Euler's formula starting with the definition
and geometric properties of multiplication in the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. In particular, a complex number z=x+iy has an absolute value defined as
and an argument defined by arg z = atan2Atan2In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
(x,y) (atan2Atan2In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
is a variant of the arctangent function). In these terms, a complex multiplication
is performed by adding the arguments (
) and multiplying the absolute values (
). (These facts are sometimes proved using Euler's theorem itself, but can alternatively be proved directly with algebra and trigonometry.) This is the basis for a two-step proof of Euler's theorem, which first calculates the absolute value of 
, and second calculates the argument of 
.
The first step is to calculate the absolute value of
:
To evaluate this, there is an approximation:
for real numbers
very close to 0. (This approximation is justified by the binomial theoremBinomial theoremIn elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
or by using calculus.) As n gets larger and larger, x2/n2 gets very close to zero, so we can use this approximation:
The second step is to calculate the argument of
. Because 
(as mentioned above), it follows that 
. Therefore,
There is an approximation:
for real numbers
very close to 0. (This approximation is related to the small-angle approximation in trigonometry, 
when 
is small and measured in radianRadianRadian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s. It can be derived using either geometry or calculus.) Therefore,
Combining these two steps,
is the complex number whose absolute value is 1 and whose argument is x. In other words, it is the point on the unit circleUnit circleIn mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
of the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
which is x radians counterclockwise from the positive real axis. This point has coordinates
in the complex plane. Therefore, 
.
Using calculus
A well-known property of the real exponential function
is that it equals its own derivative:
(where x is a real number).
The complex-valued exponential function also satisfies the same differential equation:
(where z is a complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
).
Therefore, by the chain ruleChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
:
Then define the function
Because the product rule holds for complex valued functions of a real variable for the same reason as in the real case, the derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of ƒ(x) according to the product ruleProduct ruleIn calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
is:
Therefore, ƒ(x) must be a constant functionConstant functionIn mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
in x. Because ƒ(0) = 1 by inspection, ƒ(x) = 1, giving
Multiplying both sides by cos x + i sin x, we obtain
Using differential equations
Here is another proof using calculus. The starting assumption is the same as in the previous proof:
Define a new function ƒ(x) of the real variable x as
Then we may check that
Thus ƒ(x) and eix satisfy the same first-order ordinary differential equationOrdinary differential equationIn mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
(here the complex values are considered as points in the plane ℝ2). Note also that both functions are equal to 1 at x = 0, then by the uniqueness of solutions to ordinary differential equations they must be equal everywhere (see Picard–Lindelöf theoremPicard–Lindelöf theoremIn mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...
and note the comments concerning global uniqueness in the proof section there).
See also
- Euler's identity
- Complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
- Integration using Euler's formula
- List of topics named after Leonhard Euler
External links
-
-
-
-
