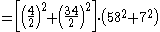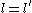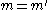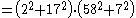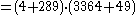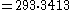Euler's factorization method
Encyclopedia
Euler's factorization method is a technique for factoring
a number by writing it as a sum of two squares in two different ways. For example the number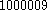
can be written as 
or as 
and Euler's method gives the factorization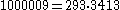 
.
The idea that two distinct representations of an odd positive integer may lead to a factorization was apparently first proposed by Marin Mersenne
. However, it was not put to use extensively until Euler one hundred years later. His most celebrated use of the method that now bears his name was to factor the number
, which apparently was previously thought to be prime even though it is not a pseudoprime
by any major primality test.
Euler's factorization method is more effective than Fermat's for integers whose factors are not close together and potentially much more efficient than trial division if one can find representations of numbers as sums of two squares reasonably easily. Euler's development ultimately permitted much more efficient factoring of numbers and, by the 1910s, the development of large factor table going up to about ten million. The methods used to find representations of numbers as sums of two squares are essentially the same as with finding differences of squares in Fermat's factorization method.
The great disadvantage of Euler's factorization method is that it cannot be applied to factoring an integer with any prime factor of the form 4k+3 occurring to an odd power in its prime factorization, as such a number can never be the sum of two squares. Even odd composite number
s of the form 4k+1 are often the product of two primes of the form 4k+3 (e.g. 3053 = 43 × 71) and again cannot be factored by Euler's method.
This restricted applicability has made Euler's factorization method disfavoured for computer
factoring algorithm
s, since any user attempting to factor a random integer is unlikely to know whether Euler's method can actually be applied to the integer in question. It is only relatively recently that there have been attempts to develop Euler's method into computer algorithms for use on specialised numbers where it is known Euler's method can be applied.
states that the product of two sums of two squares is a sum of two squares. Euler's method relies on this theorem but it can be viewed as the converse, given
we find 
as a product of sums of two squares.
First deduce that
and factor both sides to get
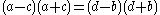(1)
Now let
and 
so that there exists some constants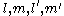 
satisfying
Substituting these into equation (1) gives
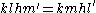
Canceling common factors and then using the fact that
and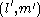 
are pairs of coprime numbers we find that
We can now apply the Brahmagupta-Fibonacci identity
to get
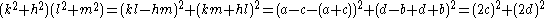
By congruence conditions, it is seen that in one of the pairs (k,h) or (l,m) both numbers are even. Without loss of generality suppose it is (k,h) then
Thus factoring
.
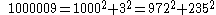
we have from the formulae above:
Thus,
1000009
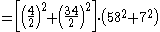
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
a number by writing it as a sum of two squares in two different ways. For example the number
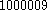can be written as or as and Euler's method gives the factorization 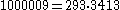.The idea that two distinct representations of an odd positive integer may lead to a factorization was apparently first proposed by Marin Mersenne
Marin Mersenne
Marin Mersenne, Marin Mersennus or le Père Mersenne was a French theologian, philosopher, mathematician and music theorist, often referred to as the "father of acoustics"...
. However, it was not put to use extensively until Euler one hundred years later. His most celebrated use of the method that now bears his name was to factor the number
, which apparently was previously thought to be prime even though it is not a pseudoprimePseudoprime
In number theory, the Fermat pseudoprimes make up the most important class of pseudoprimes that come from Fermat's little theorem.- Definition :...
by any major primality test.
Euler's factorization method is more effective than Fermat's for integers whose factors are not close together and potentially much more efficient than trial division if one can find representations of numbers as sums of two squares reasonably easily. Euler's development ultimately permitted much more efficient factoring of numbers and, by the 1910s, the development of large factor table going up to about ten million. The methods used to find representations of numbers as sums of two squares are essentially the same as with finding differences of squares in Fermat's factorization method.
The great disadvantage of Euler's factorization method is that it cannot be applied to factoring an integer with any prime factor of the form 4k+3 occurring to an odd power in its prime factorization, as such a number can never be the sum of two squares. Even odd composite number
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
s of the form 4k+1 are often the product of two primes of the form 4k+3 (e.g. 3053 = 43 × 71) and again cannot be factored by Euler's method.
This restricted applicability has made Euler's factorization method disfavoured for computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
factoring algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s, since any user attempting to factor a random integer is unlikely to know whether Euler's method can actually be applied to the integer in question. It is only relatively recently that there have been attempts to develop Euler's method into computer algorithms for use on specialised numbers where it is known Euler's method can be applied.
Theoretical Basis
The Brahmagupta-Fibonacci identityBrahmagupta-Fibonacci identity
In algebra, Brahmagupta's identity, also called Fibonacci's identity, implies that the product of two sums each of two squares is itself a sum of two squares. In other words, the set of all sums of two squares is closed under multiplication...
states that the product of two sums of two squares is a sum of two squares. Euler's method relies on this theorem but it can be viewed as the converse, given
we find as a product of sums of two squares.First deduce that
and factor both sides to get
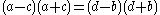(1)Now let
and so that there exists some constants 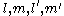satisfying-
, 
, 
-
, 
, 
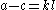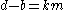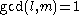
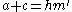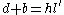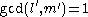
Substituting these into equation (1) gives
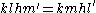
Canceling common factors and then using the fact that
and 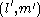are pairs of coprime numbers we find that
We can now apply the Brahmagupta-Fibonacci identity
Brahmagupta-Fibonacci identity
In algebra, Brahmagupta's identity, also called Fibonacci's identity, implies that the product of two sums each of two squares is itself a sum of two squares. In other words, the set of all sums of two squares is closed under multiplication...
to get
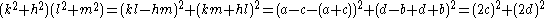
By congruence conditions, it is seen that in one of the pairs (k,h) or (l,m) both numbers are even. Without loss of generality suppose it is (k,h) then
Thus factoring
.Worked example
Since: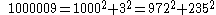we have from the formulae above:
| a = 1000 | a - c = 28 | k = 4 |
| b = 3 | a + c = 1972 | h = 34 |
| c = 972 | d - b = 232 | l = 7 |
| d = 235 | d + b = 238 | m = 58 |
Thus,
1000009
