
Ergodicity
Encyclopedia
In mathematics
, the term ergodic is used to describe a dynamical system
which, broadly speaking, has the same behavior averaged over time as averaged over space. In physics
the term is used to imply that a system satisfies the ergodic hypothesis
of thermodynamics
.
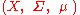 be a probability space
be a probability space
, and be a measure-preserving transformation. We say that T is ergodic with respect to
be a measure-preserving transformation. We say that T is ergodic with respect to  (or alternatively that
(or alternatively that  is ergodic with respect to T) if one of the following equivalent definitions is true:
is ergodic with respect to T) if one of the following equivalent definitions is true:
for each t ∈ R. Measurable sets invariant mod 0 under a flow or a semigroup action form the invariant subalgebra of Σ, and the corresponding measure-preserving dynamical system
is ergodic if the invariant subalgebra is the trivial σ-algebra consisting of the sets of measure 0 and their complements in X.
, a state is said to be ergodic if it is aperiodic and positive recurrent. If all states in a Markov chain are ergodic, then the chain is said to be ergodic.
is said to be ergodic if it is aperiodic and positive recurrent. If all states in a Markov chain are ergodic, then the chain is said to be ergodic.
in arithmetic. A general measure-preserving transformation or flow on a Lebesgue space admits a canonical decomposition into its ergodic components, each of which is ergodic.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the term ergodic is used to describe a dynamical system
Dynamical system (definition)
The dynamical system concept is a mathematical formalization for any fixed "rule" which describes the time dependence of a point's position in its ambient space...
which, broadly speaking, has the same behavior averaged over time as averaged over space. In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
the term is used to imply that a system satisfies the ergodic hypothesis
Ergodic hypothesis
In physics and thermodynamics, the ergodic hypothesis says that, over long periods of time, the time spent by a particle in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e., that all accessible microstates are equiprobable over a...
of thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
.
Etymology
The word ergodic is derived from the Greek words έργον and οδός, work and path. This was chosen by Boltzmann while working on a problem in statistical mechanics.Formal definition
Let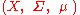 be a probability space
be a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
, and
 be a measure-preserving transformation. We say that T is ergodic with respect to
be a measure-preserving transformation. We say that T is ergodic with respect to  (or alternatively that
(or alternatively that  is ergodic with respect to T) if one of the following equivalent definitions is true:
is ergodic with respect to T) if one of the following equivalent definitions is true: - for every
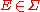 with
with  either
either 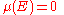 or
or 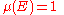 .
. - for every
 with
with 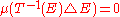 either
either  or
or 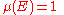 (where
(where  denotes the symmetric differenceSymmetric differenceIn mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
denotes the symmetric differenceSymmetric differenceIn mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
). - for every
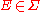 with positive measure we have
with positive measure we have 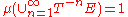 .
. - for every two sets E and H of positive measure, there exists an n > 0 such that
 .
.
Measurable flows
These definitions have natural analogues for the case of measurable flows and, more generally, measure-preserving semigroup actions. Let {Tt} be a measurable flow on (X, Σ, μ). An element A of Σ is invariant mod 0 under {Tt} iffor each t ∈ R. Measurable sets invariant mod 0 under a flow or a semigroup action form the invariant subalgebra of Σ, and the corresponding measure-preserving dynamical system
Measure-preserving dynamical system
In mathematics, a measure-preserving dynamical system is an object of study in the abstract formulation of dynamical systems, and ergodic theory in particular.-Definition:...
is ergodic if the invariant subalgebra is the trivial σ-algebra consisting of the sets of measure 0 and their complements in X.
Markov chains
In a Markov chainMarkov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
, a state
 is said to be ergodic if it is aperiodic and positive recurrent. If all states in a Markov chain are ergodic, then the chain is said to be ergodic.
is said to be ergodic if it is aperiodic and positive recurrent. If all states in a Markov chain are ergodic, then the chain is said to be ergodic.Ergodic decomposition
Conceptually, ergodicity of a dynamical system is a certain irreducibility property, akin to the notions of irreducible representation in algebra and prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
in arithmetic. A general measure-preserving transformation or flow on a Lebesgue space admits a canonical decomposition into its ergodic components, each of which is ergodic.
External links
- Outline of Ergodic Theory, by Steven Arthur Kalikow


