
Erdős–Turán conjecture on additive bases
Encyclopedia
The Erdős–Turán conjecture is an old unsolved problem in additive number theory
(not to be confused with Erdős conjecture on arithmetic progressions) posed by Paul Erdős and Pál Turán in 1941.
and Pál Turán
in. In the original paper, they state
"(2) If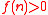 for
for  , then
, then 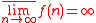 "
"
Here the function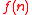 refers to the additive representation function of a given subset of the natural numbers,
refers to the additive representation function of a given subset of the natural numbers,  . In particular,
. In particular, 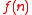 is equal to the number of ways one can write the natural number
is equal to the number of ways one can write the natural number  as the sum of two (not necessarily distinct) elements of
as the sum of two (not necessarily distinct) elements of  . If
. If  is always positive for sufficiently large
is always positive for sufficiently large  , then
, then  is called an additive basis (of order 2). This problem has attracted significant attention, but remains unsolved.
is called an additive basis (of order 2). This problem has attracted significant attention, but remains unsolved.
 , we define its representation function
, we define its representation function 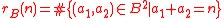 . Then the conjecture states that if
. Then the conjecture states that if 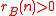 for all
for all  sufficiently large, then
sufficiently large, then  .
.
More generally, for any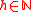 and subset
and subset  , we can define the
, we can define the  representation function as
representation function as  . We say that
. We say that  is an additive basis of order
is an additive basis of order 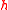 if
if 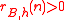 for all
for all  sufficiently large. One can see from an elementary argument that if
sufficiently large. One can see from an elementary argument that if  is an additive basis of order
is an additive basis of order 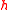 , then
, then
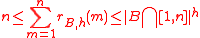
So we obtain the lower bound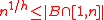 .
.
The original conjecture spawned as Erdős and Turán sought a partial answer to Sidon's problem (see: Sidon sequence). Later, Erdős set out to answer the following question posed by Sidon: how close to the lower bound can an additive basis
can an additive basis  of order
of order  get? This question was answered positively in the case
get? This question was answered positively in the case  by Erdős in 1956. Erdős proved that there exists an additive basis
by Erdős in 1956. Erdős proved that there exists an additive basis  of order 2 and constants
of order 2 and constants 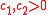 such that
such that 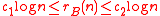 for all
for all  sufficiently large. In particular, this implies that there exists an additive basis
sufficiently large. In particular, this implies that there exists an additive basis  such that
such that  , which is essentially best possible. This motivated Erdős to make the following conjecture
, which is essentially best possible. This motivated Erdős to make the following conjecture
If is an additive basis of order
is an additive basis of order 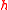 , then
, then 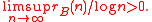
In 1986, Eduard Wirsing proved that a large class of additive bases, including the prime numbers, contains a subset that is an additive basis but significantly thinner than the original. In 1990, Erdős and Tetalli extended Erdős's 1956 result to bases of arbitrary order. In 2000, V. Vu
proved that thin subbases exist in the Waring bases using the Hardy–Littlewood circle method and his polynomial concentration results. In 2006, Borwein, Choi, and Chu proved that for all additive bases ,
,  eventually exceeds 7.
eventually exceeds 7.
Additive number theory
In number theory, the specialty additive number theory studies subsets of integers and their behavior under addition. More abstractly, the field of "additive number theory" includes the study of Abelian groups and commutative semigroups with an operation of addition. Additive number theory has...
(not to be confused with Erdős conjecture on arithmetic progressions) posed by Paul Erdős and Pál Turán in 1941.
History
The conjecture was made jointly by Paul ErdősPaul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
and Pál Turán
Pál Turán
Paul Turán was a Hungarian mathematician who worked primarily in number theory. He had a long collaboration with fellow Hungarian mathematician Paul Erdős, lasting 46 years and resulting in 28 joint papers.- Life and education :...
in. In the original paper, they state
"(2) If
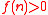 for
for  , then
, then 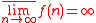 "
"Here the function
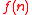 refers to the additive representation function of a given subset of the natural numbers,
refers to the additive representation function of a given subset of the natural numbers,  . In particular,
. In particular, 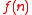 is equal to the number of ways one can write the natural number
is equal to the number of ways one can write the natural number  as the sum of two (not necessarily distinct) elements of
as the sum of two (not necessarily distinct) elements of  . If
. If  is always positive for sufficiently large
is always positive for sufficiently large  , then
, then  is called an additive basis (of order 2). This problem has attracted significant attention, but remains unsolved.
is called an additive basis (of order 2). This problem has attracted significant attention, but remains unsolved.Progress
While the conjecture remains unsolved, there have been significant advance on the problem. First, we express the problem in modern language. For a given subset , we define its representation function
, we define its representation function 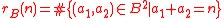 . Then the conjecture states that if
. Then the conjecture states that if 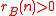 for all
for all  sufficiently large, then
sufficiently large, then  .
.More generally, for any
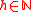 and subset
and subset  , we can define the
, we can define the  representation function as
representation function as  . We say that
. We say that  is an additive basis of order
is an additive basis of order 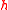 if
if 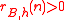 for all
for all  sufficiently large. One can see from an elementary argument that if
sufficiently large. One can see from an elementary argument that if  is an additive basis of order
is an additive basis of order 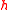 , then
, then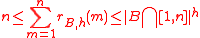
So we obtain the lower bound
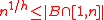 .
.The original conjecture spawned as Erdős and Turán sought a partial answer to Sidon's problem (see: Sidon sequence). Later, Erdős set out to answer the following question posed by Sidon: how close to the lower bound
 can an additive basis
can an additive basis  of order
of order  get? This question was answered positively in the case
get? This question was answered positively in the case  by Erdős in 1956. Erdős proved that there exists an additive basis
by Erdős in 1956. Erdős proved that there exists an additive basis  of order 2 and constants
of order 2 and constants 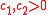 such that
such that 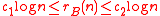 for all
for all  sufficiently large. In particular, this implies that there exists an additive basis
sufficiently large. In particular, this implies that there exists an additive basis  such that
such that  , which is essentially best possible. This motivated Erdős to make the following conjecture
, which is essentially best possible. This motivated Erdős to make the following conjectureIf
 is an additive basis of order
is an additive basis of order 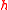 , then
, then 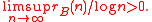
In 1986, Eduard Wirsing proved that a large class of additive bases, including the prime numbers, contains a subset that is an additive basis but significantly thinner than the original. In 1990, Erdős and Tetalli extended Erdős's 1956 result to bases of arbitrary order. In 2000, V. Vu
Van H. Vu
Van H. Vu is a Vietnamese mathematician, a professor of mathematics at Yale University and the 2008 winner of the Pólya Prize of the Society for Industrial and Applied Mathematics for his work on concentration of measure. He is a collaborator of Terence Tao....
proved that thin subbases exist in the Waring bases using the Hardy–Littlewood circle method and his polynomial concentration results. In 2006, Borwein, Choi, and Chu proved that for all additive bases
 ,
,  eventually exceeds 7.
eventually exceeds 7.

