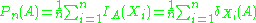Empirical measure
Encyclopedia
In probability theory
, an empirical measure is a random measure arising from a particular realization of a (usually finite) sequence of random variable
s. The precise definition is found below. Empirical measures are relevant to mathematical statistics
.
The motivation for studying empirical measures is that it is often impossible to know the true underlying probability measure
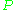. We collect observations 
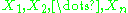and compute relative frequencies. We can estimate 
, or a related distribution function 
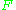by means of the empirical measure or empirical distribution function, respectively. These are uniformly good estimates under certain conditions. Theorems in the area of empirical process
es provide rates of this convergence.
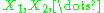be a sequence of independent identically distributed random variable
s with values in the state space S with probability measure
P.
Definition
For a fixed measurable set A, nPn(A) is a binomial random variable with mean nP(A) and variance nP(A)(1 − P(A)). In particular,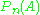
is an unbiased estimator
of P(A).
Definition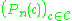
is the empirical measure indexed by 
, a collection of measurable subsets of S.
To generalize this notion further, observe that the empirical measure Pn maps measurable function
s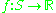
to their empirical mean,
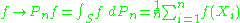
In particular, the empirical measure of A is simply the empirical mean of the indicator function,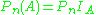
.
For a fixed measurable function f,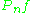
is a random variable with mean 
and variance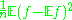 
.
By the strong law of large numbers
,
converges to P(A) almost surely
for fixed A. Similarly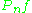
converges to 
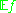almost surely for a fixed measurable function f. The problem of uniform convergence of 
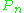to P was open until Vapnik and Chervonenkis solved it in 1968.
If the class
(or 
) is Glivenko–Cantelli with respect to P then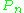 
converges to P uniformly over 
(or 
). In other words, with probability 1 we have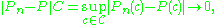
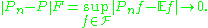
it is given by
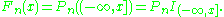
In this case, empirical measures are indexed by a class
It has been shown that 
is a uniform Glivenko–Cantelli class, in particular,
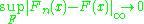
with probability 1.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, an empirical measure is a random measure arising from a particular realization of a (usually finite) sequence of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s. The precise definition is found below. Empirical measures are relevant to mathematical statistics
Mathematical statistics
Mathematical statistics is the study of statistics from a mathematical standpoint, using probability theory as well as other branches of mathematics such as linear algebra and analysis...
.
The motivation for studying empirical measures is that it is often impossible to know the true underlying probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
. We collect observations 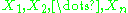and compute relative frequencies. We can estimate , or a related distribution function 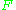by means of the empirical measure or empirical distribution function, respectively. These are uniformly good estimates under certain conditions. Theorems in the area of empirical processEmpirical process
The study of empirical processes is a branch of mathematical statistics and a sub-area of probability theory. It is a generalization of the central limit theorem for empirical measures...
es provide rates of this convergence.
Definition
Let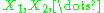 be a sequence of independent identically distributed random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s with values in the state space S with probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
P.
Definition
- The empirical measure
is defined for measurable subsets of S and given by
- where
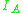is the indicator function and 
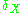is the Dirac measure.
For a fixed measurable set A, nPn(A) is a binomial random variable with mean nP(A) and variance nP(A)(1 − P(A)). In particular,
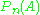is an unbiased estimatorBias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
of P(A).
Definition
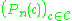is the empirical measure indexed by , a collection of measurable subsets of S.To generalize this notion further, observe that the empirical measure Pn maps measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
s
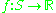to their empirical mean,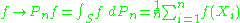In particular, the empirical measure of A is simply the empirical mean of the indicator function,
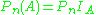.For a fixed measurable function f,
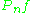is a random variable with mean and variance 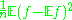.By the strong law of large numbers
Law of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
,
converges to P(A) almost surelyAlmost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
for fixed A. Similarly
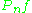converges to 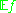almost surely for a fixed measurable function f. The problem of uniform convergence of 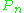to P was open until Vapnik and Chervonenkis solved it in 1968.If the class
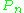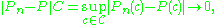
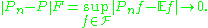
(or ) is Glivenko–Cantelli with respect to P then converges to P uniformly over (or ). In other words, with probability 1 we haveEmpirical distribution function
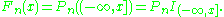
The empirical distribution function provides an example of empirical measures. For real-valued iid random variables it is given byIn this case, empirical measures are indexed by a class
It has been shown that is a uniform Glivenko–Cantelli class, in particular,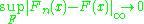with probability 1.